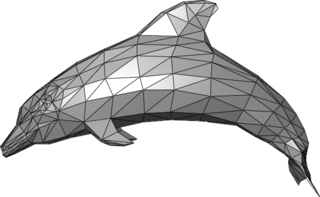
Алгоритм Катмулла — Кларка

Алгоритм Катмулла — Кларка — это техника, используемая в компьютерной графике для создания гладких поверхностей путём моделирования подразделения поверхности[англ.]. Алгоритм разработали Эдвин Катмулл и Джеймс Кларк в 1978 как обобщение бикубических однородных B-сплайновых поверхностей для произвольной топологии[1]. В 2005 году Эдвин Катмулл получил премию Американской академии за технические достижения[англ.] вместе с Тони Дероузом и Джосом Стэмом[англ.] за их разработки в области подразделения поверхностей.
Рекурсивные вычисления
Поверхности Катмулла — Кларка определяются рекурсивно, используя следующую схему последовательных уточнений[1]:
Начинаем с сетки в виде произвольного многогранника. Все вершины этой сетки будем называть исходными точками.
- Для каждой грани добавляем точку грани
- Выбираем в качестве точки грани среднее всех исходных точек соответствующей грани.
- Для каждого ребра добавляем точку ребра.
- Выбираем в качестве точки ребра среднее из двух соседних точек грани и двух исходных конечных точек ребра.
- Для каждой точки грани, добавим ребро для каждого ребра грани, соединяя точку грани с точкой ребра для грани.
- Для каждой исходной точки P берём среднее F для всех n (вновь созданных) точек граней для граней, касающихся P, и берём среднее R всех n точек рёбер для (исходных) рёбер, касающихся P, где середина каждого ребра является средним двух конечных вершин (не путать с новыми «точками рёбер», определёнными выше). Переносим каждую исходную точку в точку
- Эта точка является барицентром точек P, R и F с весами (n − 3), 2 и 1.
- Соединяем каждую новую точку с новыми точками рёбер всех исходных рёбер, инцидентных исходной вершине.
- Определяем новые грани, заключённые новыми рёбрами.
Новая сетка состоит только из четырёхугольников, которые, вообще говоря, не находятся в одной плоскости. Новая сетка, в общем случае, будет выглядеть более гладко, чем исходная.
Повторное подразбиение приводит к более гладкой сетке. Можно показать, что предельная поверхность, полученная этим методом, по меньшей мере принадлежит классу в особых точках и во всех остальных местах (здесь n означает число непрерывных производных, когда мы говорим о ). После итерации число особых точек на поверхности не изменяется.
Формулу для барицентра Катмулл и Кларк выбрали, исходя из эстетических, а не математических, соображений, хотя Катмулл и Кларк приложили большие усилия, чтобы строго доказать, что метод сходится к бикубическим B-сплайновым поверхностям[1].
Точные вычисления
Результирующая подразделённая поверхность Катмулла — Кларка может быть получена прямо без последовательных улучшений. Это можно сделать с помощью техники Джоса Стэма[англ.][2]. Этот метод переформулирует процесс последовательных приближений в задачу вычисления экспоненты матрицы, которую можно решить путём диагонализации матрицы.
Программное обеспечение, использующее подразделение поверхностей методом Катмулла — Кларка
- 3ds Max
- 3D-Coat
- AC3D[англ.]
- Anim8or[англ.]
- AutoCAD
- Blender
- Carrara[англ.]
- CATIA
- CGAL[англ.]
- Cheetah3D[англ.]
- Cinema 4D
- Clara.io[англ.]
- Creo (Freestyle)[англ.][3]
- DAZ Studio, 2.0
- Gelato[англ.]
- Hammer
- Hexagon[англ.]
- Houdini
- K-3D
- LightWave 3D, version 9
- Makehuman[англ.]
- Maya
- Metasequoia[англ.]
- MODO
- Mudbox
- Pixar's OpenSubdiv[4][5][6][7][8]
- PRMan
- Realsoft3D[англ.]
- Remo 3D[англ.]
- Shade[англ.]
- Rhinoceros 3D — Grasshopper 3D Plugin — Weaverbird Plugin
- Silo
- SketchUp — Требуется Plugin.
- Softimage XSI
- Strata 3D CX[англ.]
- Wings 3D
- Zbrush
Примечания
- ↑ 1 2 3 Catmull, Clark, 1978, с. 350.
- ↑ Stam, 1998, с. 395–404.
- ↑ Архивированная копия. Дата обращения: 18 августа 2017. Архивировано из оригинала 23 ноября 2016 года.
- ↑ Manuel Kraemer. OpenSubdiv: Interoperating GPU Compute and Drawing // Multithreading for Visual Effects (англ.) / Martin Watt, Erwin Coumans, George ElKoura, Ronald Henderson, Manuel Kraemer, Jeff Lait, James Reinders. — CRC Press, 2014. — P. 163—199. — ISBN 978-1-4822-4356-7.
- ↑ Meet the Experts: Pixar Animation Studios, The OpenSubdiv Project - YouTube. Дата обращения: 18 августа 2017. Архивировано 26 января 2017 года.
- ↑ Pixar’s OpenSubdiv V2: a detailed look | fxguide. Дата обращения: 18 августа 2017. Архивировано 30 июля 2017 года.
- ↑ Архивированная копия. Дата обращения: 18 августа 2017. Архивировано 12 марта 2018 года.
- ↑ OpenSubdiv Blender demo - YouTube. Дата обращения: 18 августа 2017. Архивировано 7 января 2016 года.
Литература
- Catmull E., Clark J. Recursively generated B-spline surfaces on arbitrary topological meshes // Computer-Aided Design. — 1978. — Т. 10, вып. 6. — С. 350. — doi:10.1016/0010-4485(78)90110-0.
- Stam J. Proceedings of the 25th annual conference on Computer graphics and interactive techniques - SIGGRAPH '98. — 1998. — С. 395—404. — ISBN 0-89791-999-8. — doi:10.1145/280814.280945. Архивная копия от 9 мая 2018 на Wayback Machine
Литература для дальнейшего чтения
- Derose T., Kass M., Truong T. Subdivision surfaces in character animation // Proceedings of the 25th annual conference on Computer graphics and interactive techniques - SIGGRAPH '98. — 1998. — С. 85. — ISBN 0897919998. — doi:10.1145/280814.280826.
- Loop C., Schaefer S. Approximating Catmull-Clark subdivision surfaces with bicubic patches // ACM Transactions on Graphics. — 2008. — Т. 27. — С. 1. — doi:10.1145/1330511.1330519.
- Kovacs D., Mitchell J., Drone S., Zorin D. Real-Time Creased Approximate Subdivision Surfaces with Displacements // IEEE Transactions on Visualization and Computer Graphics. — 2010. — Т. 16, вып. 5. — С. 742. — doi:10.1109/TVCG.2010.31. — PMID 20616390.
- Matthias Nießner, Charles Loop, Mark Meyer, Tony DeRose. Feature Adaptive GPU Rendering of Catmull-Clark Subdivision Surfaces // ACM Transactions on Graphics. — 2012. — Январь (т. 31, вып. 1). — doi:10.1145/2077341.2077347., Видеоролик
- Nießner Matthias, Loop Charles, Greiner Günther. Efficient Evaluation of Semi-Smooth Creases in Catmull-Clark Subdivision Surfaces // Eurographics 2012 Annex: Short Papers (Eurographics 2012, Cagliary). — 2012. — С. pp 41—44.
- Wade Brainerd. Tessellation in Call of Duty: Ghosts. Видеоролик с докладом, доступен также PDF документ
- Doo D., Sabin M. Behavior of recursive division surfaces near extraordinary points // Computer-Aided Design. — 1978. — Т. 10, вып. 6. — doi:10.1016/0010-4485(78)90111-2.