Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся. Четырёхугольник без самопересечений называется простым, часто под термином «четырёхугольник» имеются в виду только простые четырёхугольники.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.
В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как
,
Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.
Цили́ндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Проекция — это:
- изображение трёхмерной фигуры на так называемой картинной (проекционной) плоскости способом, представляющим собой геометрическую идеализацию оптических механизмов зрения, фотографии, камеры-обскуры. Термин проекция в этом контексте также означает метод построения такого изображения и технические приёмы, в основе которых лежит этот метод. Широко применяется в инженерной графике, архитектуре, живописи и картографии. Изучением методов построения проекций как инженерная дисциплина занимается начертательная геометрия;
- обобщение проекции в первом её смысле для отображения точек, фигур, векторов пространства любой размерности на его подпространство любой размерности: например, кроме проекции точек трёхмерного пространства на плоскость, может быть проекция точек трёхмерного пространства на прямую, точек плоскости на прямую, точек 7-мерного пространства на его 4-мерное подпространство и т. п., а также проекция вектора на любое подпространство исходного пространства, в особенности на прямую или на направление вектора. Проекция в этом смысле находит широкое применение в отношении векторов, при использовании декартовых координат и т. п.
Айвен Эдвард Сазерленд — американский учёный в области информатики и пионер интернета. Получил премию Тьюринга от ACM в 1988 за создание «Sketchpad» — прообраза будущих САПР, имеющего ранний прототип графического интерфейса. Одновременно впервые применил объектно-ориентированный подход к программированию. В 2012 был удостоен премии Киото за ту же разработку.
Начерта́тельная геоме́трия — инженерная дисциплина, представляющая двумерный геометрический аппарат и набор алгоритмов для исследования свойств геометрических объектов.
В вычислительной геометрии известна задача об определении принадлежности точки многоугольнику. На плоскости даны многоугольник и точка. Требуется решить вопрос о принадлежности точки многоугольнику.
Плана́рный граф — граф, который можно изобразить на плоскости без пересечений рёбер не по вершинам. Какое-либо конкретное изображение планарного графа на плоскости без пересечения рёбер не по вершинам называется плоским графом. Иначе говоря, планарный граф изоморфен некоторому плоскому графу, изображённому на плоскости так, что его вершины — это точки плоскости, а рёбра — кривые на плоскости, которые если и пересекаются между собой, то только по вершинам. Области, на которые граф разбивает плоскость, называются его гранями. Неограниченная часть плоскости — тоже грань, называемая внешней гранью. Любой плоский граф может быть спрямлён, то есть перерисован на плоскости так, что все его рёбра будут отрезками прямых.
Двоичное разбиение пространства — метод рекурсивного разбиения евклидова пространства в выпуклые множества и гиперплоскости. В результате объекты получают представление в виде структуры данных, называемой BSP-деревом.
Вычислительная геометрия — раздел информатики, в котором рассматриваются алгоритмы для решения геометрических задач.
Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
G-код — условное именование языка программирования устройств с числовым программным управлением (ЧПУ). Был создан компанией Electronic Industries Alliance в начале 1960-х. Окончательная доработка была одобрена в феврале 1980 года как стандарт RS274D. Комитет ISO утвердил G-код как стандарт ISO 6983-1:2009, Госкомитет по стандартам СССР — как ГОСТ 20999-83. В советской технической литературе G-код обозначается как код ИСО 7-бит, это вызвано тем, что G-код кодировали на 8-дорожечную перфоленту в коде ISO 7-bit, восьмая дорожка использовалась для контроля чётности.
Обнаружение столкновений — вычислительная проблема обнаружения пересечений между собой двух или больше объектов. Тема чаще всего связана с её использованием в физических движках, компьютерной анимации и робототехнике. В дополнение к определению, столкнулись ли два объекта, системы обнаружения столкновений могут вычислить время воздействия и сообщить о коллекторе контакта. Ответ на столкновение зависит от используемого моделирования. Решение проблем обнаружения столкновений требует широкого применения понятий из линейной алгебры и вычислительной геометрии. Алгоритмы обнаружения столкновений являются одним из основных составляющих трёхмерных компьютерных игр.
Алгоритм Бентли — Оттманна (1979) позволяет найти все точки пересечений прямолинейных отрезков на плоскости. В нем применяется метод выметающей прямой. В методе используется вертикальная выметающая прямая, движущаяся слева направо, при этом отрезки, которые она пересекает при данной координате 
, можно упорядочить по координате 
, тем самым их можно сравнивать между собой. Это сравнение можно осуществить, например, используя уравнение прямой, проходящей через две точки : 
, где 
, 
и 
, 
— координаты, соответственно, первой и второй точек отрезка. Выметающая прямая перемещается по так называемым точкам событий. После точки пересечения отрезки следует менять местами, так как, например, самый верхний из пересекающихся отрезков после точки пересечения становится самым нижним. Приведенный ниже алгоритм не рассчитан на случай, когда два отрезка пересекаются больше, чем в одной точке.
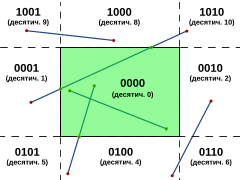
Алгоритм Кируса — Бека — алгоритм отсечения отрезков произвольным выпуклым многоугольником. Был предложен в качестве более эффективной замены алгоритма Коэна — Сазерленда, который выполняет отсечение за несколько итераций.
Аксиоматика Александрова — система аксиом Евклидовой геометрии, предложенная Александром Даниловичем Александровым. Эта аксиоматика частично использовалась в учебнике по геометрии написанного Александровым совместно с Алексеем Леонидовичем Вернером и Валерием Идельевичем Рыжиком.
Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек.
Отсечение отрезков — это процесс в компьютерной графике удаления прямых или частей прямых вне зоны внимания. Обычно любая прямая или часть прямой, не принадлежащая видимой области, удаляется.
