Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как
 ,
,
Звезда — вид плоских невыпуклых многоугольников, не имеющий однозначного математического определения.

R-дерево — древовидная структура данных (дерево), предложенная в 1984 году Антонином Гуттманом. Она подобна B-дереву, но используется для организации доступа к пространственным данным, то есть для индексации многомерной информации, такой, например, как географические данные с двумерными координатами. Типичным запросом с использованием R-деревьев мог бы быть такой: «Найти все музеи в пределах 2 километров от моего текущего местоположения».
В вычислительной геометрии известна задача об определении принадлежности точки многоугольнику. На плоскости даны многоугольник и точка. Требуется решить вопрос о принадлежности точки многоугольнику.

Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.
Двоичное разбиение пространства — метод рекурсивного разбиения евклидова пространства в выпуклые множества и гиперплоскости. В результате объекты получают представление в виде структуры данных, называемой BSP-деревом.
Вычислительная геометрия — раздел информатики, в котором рассматриваются алгоритмы для решения геометрических задач.
Алгоритм Грэхема — алгоритм построения выпуклой оболочки в двумерном пространстве. В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки.
Построение выпуклой оболочки методом «разделяй и властвуй» — алгоритм построения выпуклой оболочки.
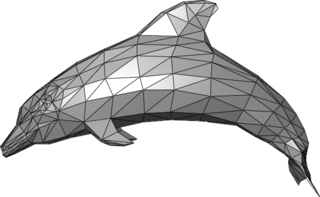
Полигональная сетка — это совокупность вершин, рёбер и граней, которые определяют форму многогранного объекта в трёхмерной компьютерной графике и объёмном моделировании. Гранями обычно являются треугольники, четырёхугольники или другие простые выпуклые многоугольники (полигоны), так как это упрощает рендеринг, но сетки могут также состоять и из наиболее общих вогнутых многоугольников[прояснить], или многоугольников с отверстиями.

Выпуклый многогранник — многогранник, являющийся выпуклым множеством. Это основное понятие в задачах линейного программирования.
Положительно ориентированной кривой в математике называется плоская простая замкнутая кривая такая, что при перемещении по ней внутренность кривой всегда находится слева. Если в вышеприведённом определении поменять местами «лево» и «право», оно определяет отрицательно ориентированную кривую.
Алгоритм Кируса — Бека — алгоритм отсечения отрезков произвольным выпуклым многоугольником. Был предложен в качестве более эффективной замены алгоритма Коэна — Сазерленда, который выполняет отсечение за несколько итераций.
Трекл — вложение графа в плоскость таким образом, что каждое ребро является кривой Жордана и каждая пара рёбер пересекается равно раз. Рёбра могут пересекаться по общей вершине, либо, если они не имеют общих вершин, во внутренних точках. В последнем случае предполагается, что пересечение трансверсально.

Простой многоугольник — это фигура, состоящая из непересекающихся отрезков («сторон»), соединённых попарно с образованием замкнутого пути. Если стороны пересекаются, многоугольник не является простым. Часто слово «простой» опускается из вышеприведённого определения.

Многоугольник видимости или область видимости для точки p на плоскости среди препятствий — это многоугольная область всех точек плоскости, видимых из точки p. Многоугольник видимости можно определить для видимости из отрезка или многоугольника. Многоугольники видимости полезны в робототехнике, компьютерных играх и для определения позиций объектов, например, для определения наилучшего расположения охраны в картинных галереях.

Отсечение отрезков — это процесс в компьютерной графике удаления прямых или частей прямых вне зоны внимания. Обычно любая прямая или часть прямой, не принадлежащая видимой области, удаляется.
















