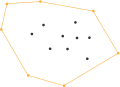
Выпуклой оболочкой множества 
называется наименьшее выпуклое множество, содержащее . «Наименьшее множество» здесь означает наименьший элемент по отношению к вложению множеств, то есть такое выпуклое множество, содержащее данную фигуру, что оно содержится в любом другом выпуклом множестве, содержащем данную фигуру.
Выпуклое множество в аффинном или векторном пространстве — множество, в котором все точки отрезка, образуемого любыми двумя точками данного множества, также принадлежат данному множеству.
Метод эллипсоидов — алгоритм нахождения точки, лежащей в пересечении выпуклых множеств. Разработан А. С. Немировским и доведён до алгоритмической реализации Л. Г. Хачияном в ВЦ АН СССР.
Откры́тые (нерешённые) математи́ческие пробле́мы — задачи, которые рассматривались математиками, но до сих пор не решены. Часто имеют форму гипотез, которые предположительно верны, но нуждаются в доказательстве.
Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.
Вычислительная геометрия — раздел информатики, в котором рассматриваются алгоритмы для решения геометрических задач.
Алгоритм Грэхема — алгоритм построения выпуклой оболочки в двумерном пространстве. В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки.
Построение выпуклой оболочки методом «разделяй и властвуй» — алгоритм построения выпуклой оболочки.
Триангуля́ция Делоне́ — триангуляция для заданного множества точек S на плоскости, при которой для любого треугольника все точки из S за исключением точек, являющихся его вершинами, лежат вне окружности, описанной вокруг треугольника. Обозначается DT(S). Впервые описана в 1934 году советским математиком Борисом Делоне.
Лемма Шепли — Фолкмана связывает две операции выпуклой геометрии — сложение по Минковскому и выпуклую оболочку. Лемма имеет приложения в ряде дисциплин, в том числе в математической экономике, оптимизации и теории вероятностей. Лемма и связанные с ней результаты позволяют дать утвердительный ответ на вопрос «Близка ли к состоянию выпуклости сумма нескольких множеств?».
Основная теорема о рекуррентных соотношениях используется в анализе алгоритмов для получения асимптотической оценки рекурсивных соотношений, часто возникающих при анализе алгоритмов типа «разделяй и властвуй», например, при оценке времени их выполнения. Теорема была введена и доказана Джоном Бентли, Доротеном Хакеном и Джеймсом Хакеном в 1980 году. Теорема была популяризована в книге Алгоритмы: построение и анализ, в которой она была приведена.
Задача о размещении объектов, известная также как анализ расположения оборудования или задача k-центра, — это ветвь исследования операций и вычислительной геометрии, исследующей оптимальное расположение объектов с целью минимизировать цены перевозок с учётом таких ограничений, как размещение опасных материалов вблизи жилищ. Техника применима также к кластерному анализу.
Задача о наименьшей окружности или задача о минимальном покрывающем круге — задача о вычислении наименьшей окружности, содержащей все заданные точки из множества на евклидовой плоскости. Соответствующая задача в n-мерном пространстве, задача о наименьшей ограничивающей сфере, вычисляет наименьшую гиперсферу, содержащую все точки заданного множества. Задачу о наименьшей окружности первым поставил английский математик Джеймс Джозеф Сильвестр в 1857.
Онлайновое машинное обучение — это метод машинного обучения, в котором данные становятся доступными в последовательном порядке и используются для обновления лучшего предсказания для последующих данных, выполняемого на каждом шаге обучения. Метод противоположен пакетной технике обучения, в которой лучшее предсказание генерируется за один раз, исходя из полного тренировочного набора данных. Онлайновое обучение является общей техникой, используемой в областях машинного обучения, когда невозможна тренировка по всему набору данных, например, когда возникает необходимость в алгоритмах, работающих с внешней памятью. Метод используется также в ситуациях, когда алгоритму приходится динамически приспосабливать новые схемы в данных или когда сами данные образуются как функция от времени, например, при предсказании цен на фондовом рынке. Алгоритмы онлайнового обучения могут быть склонны к катастрофическим помехам, проблеме, которая может быть решена с помощью подхода пошагового обучения.
Евклидово минимальное остовное дерево — это минимальное остовное дерево набора из n точек на плоскости, где вес ребра между любой парой точек является евклидовым расстоянием между двумя точками. Простыми терминами, EMST связывает набор точек с помощью отрезков так, что общая длина всех отрезков минимальна и любая точка может быть достигнута из другой точки по этим отрезкам.
Задача о паре ближайших точек — это задача вычислительной геометрии. Дано n точек в метрическом пространстве, нужно найти пару точек с наименьшим расстоянием между ними.
Теорема о бутерброде утверждает, что если дано n измеримых «объектов» в n-мерном евклидовом пространстве, их можно разделить пополам (согласно их мере, то есть объёме) с помощью одной (n − 1)-мерной гиперплоскости.
Теорема о верхней границе утверждает, что циклические многогранники имеют наибольшее возможное число граней среди всех выпуклых многогранников и триангуляций многомерной сферы при любой заданной размерности пространства и любом числе вершин. Это один из важнейших результатов в комбинаторике многогранников.
