
Правильный многогранник или плато́ново тело — это выпуклый многогранник, грани которого являются равными правильными многоугольниками, обладающий пространственной симметрией следующего типа: все многогранные углы при его вершинах правильные и равны друг другу.

Тригонометри́ческие фу́нкции — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе. Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.

Купол — тело, образованное соединением двух многоугольников, в котором один (основание) имеет вдвое больше сторон по сравнению с другим. Соединение многоугольников осуществляется равнобедренными треугольниками и прямоугольниками. Если треугольники правильные, а прямоугольники являются квадратами, в то время как основание и вершина являются правильными многоугольниками, купол является многогранником Джонсона. Эти куполы, трёхскатный, четырёхскатный и пятискатный, можно получить, взяв сечения кубооктаэдра, ромбокубооктаэдра и ромбоикосододекаэдра соответственно.

Скру́ченно удлинённая четырёхуго́льная пирами́да — один из многогранников Джонсона.
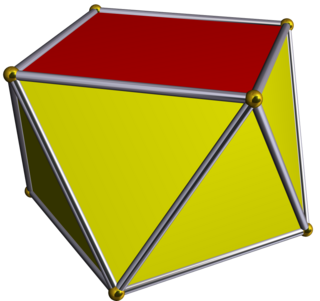
Квадратная антипризма (антикуб) — второй многогранник в бесконечном ряду антипризм, образованных последовательностью треугольных граней, закрытых с обеих сторон многоугольниками. Если все грани являются правильными многоугольниками, антипризма является полуправильным многогранником или однородным многогранником.

Скру́ченно удлинённая пятиуго́льная пирами́да, или отсечённый икоса́эдр — один из многогранников Джонсона.

Скру́ченный ромбоикосододека́эдр — один из многогранников Джонсона.

Два́жды противополо́жно скру́ченный ромбоикосододека́эдр — один из многогранников Джонсона.
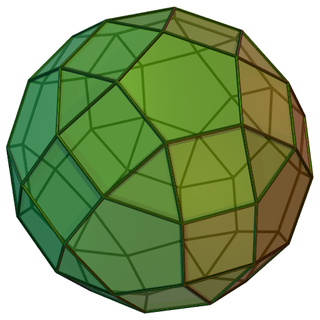
Два́жды ко́со скру́ченный ромбоикосододека́эдр — один из многогранников Джонсона.

Три́жды скру́ченный ромбоикосододека́эдр — один из многогранников Джонсона.

Два́жды ко́со скру́ченный отсечённый ромбоикосододека́эдр — один из многогранников Джонсона.

Скру́ченно удлинённая пятиска́тная куполорото́нда — один из многогранников Джонсона.

Скру́ченно удлинённая пятиска́тная бирото́нда — один из многогранников Джонсона.
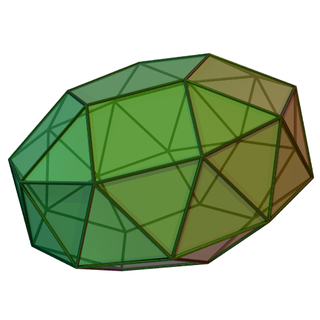
Скру́ченно удлинённый пятиска́тный бику́пол — один из многогранников Джонсона.

Скру́ченно удлинённый трёхска́тный бику́пол — один из многогранников Джонсона.

Скру́ченно удлинённый четырёхска́тный бику́пол — один из многогранников Джонсона.
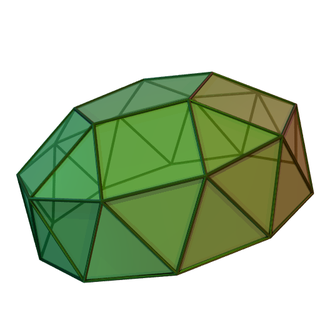
Скру́ченно удлинённый пятиска́тный ку́пол — один из многогранников Джонсона.

Скру́ченно удлинённая пятиска́тная рото́нда — один из многогранников Джонсона.

В данной статье приведены точные алгебраические выражения для некоторых тригонометрических чисел. Такие выражения могут потребоваться, например, для приведения результатов выражений с тригонометрическими функциями в радикальную форму, что даёт возможность для дальнейшего упрощения.
Эта страница основана на
статье Википедии.
Текст доступен на условиях лицензии
CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.













































