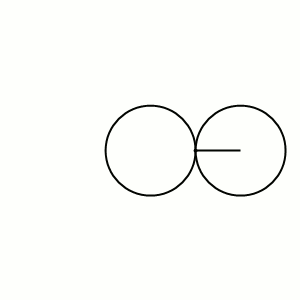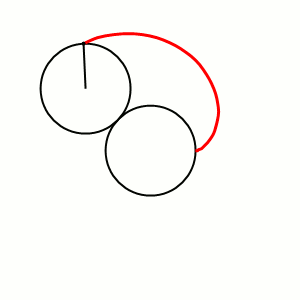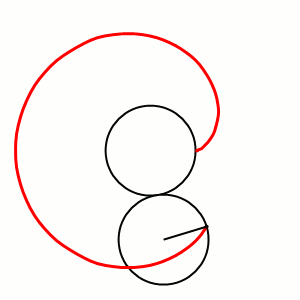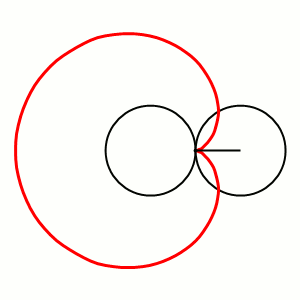Аньезиана

Аньезиа́на (англ. agnesiana — кривая Аньези[1]) (частный случай — верзие́ра[2][3][4]) — гиперболизм окружности с полюсом на этой окружности и произвольной прямой, перпендикулярной диаметру окружности с концом на полюсе[5][6].
В декартовых координатах аньезиана — это гиперболизм окружности
с радиусом и полюсом в начале координат на окружности и прямой , имеющий следующее уравнение[5][6]:
или
или
Полагают, что : при аньезиана вырождается в ось абсцисс[7][5].
Относится к плоским алгебраически кривым 3-го порядка[4][8].
Аньезиана — это кривая, обладающая следующими простыми свойствами[3][5][9][8]:
- неограниченная;
- имеет одну асимптоту.
- связная;
- имеет бесконечно удалённую изолированную точку в направлении оси ординат;
- особых точек нет;
- имеет одну ось симметрии.
Образующая окружность есть антигиперболизм аньезианы[10].
Своё название аньезиана получила в честь итальянского математика Марии Гаэтаны Аньези, исследовавшей частный случай этой кривой — верзиеру — в 1748 году[9][11][4][7][12][13]. Ранее верзиеру изучали Пьер Ферма в 1630 году и Гвидо Гранди в 1703 году[3].
Определения аньезианы
Определение и уравнение
Аньезиа́на (англ. agnesiana — кривая Аньези[1]) — гиперболизм окружности, ограниченный тем, что его полюс расположен на этой окружности, и произвольной прямой, перпендикулярной диаметру окружности с концом на полюсе[5][6]. Эта окружность называется образующей[7], или производящей[8][14]. Точка образующей окружности, диаметрально противоположная полюсу, называется вершиной аньезианы[11].
В декартовых координатах аньезиана — это гиперболизм окружности
с радиусом ограниченный тем, что его полюс расположен на окружности, куда удобно поместить также и начало координат, и произвольной прямой . Такой гиперболизм окружности записывается уравнением, полученным из уравнения окружности[5][6]:
или
или
Полагают, что , поскольку при аньезиана вырождается в прямую — ось абсцисс[7][5].
Относится к плоским алгебраически кривым 3-го порядка[4][8].
Аньезиана — это кривая, обладающая следующими простыми свойствами[3][5][9][8]:
- неограниченная;
- имеет одну асимптоту.
- связная;
- имеет бесконечно удалённую изолированную точку в направлении оси ординат;
- особых точек нет;
- имеет одну ось симметрии.
Приведённое выше уравнение аньезианы в декартовой системе координат
(с площадью области, ограниченной кривой и асимптотой [5]) может быть записано по-другому:
- где — диаметр базовой окружности гиперболизма (и площадью [5]);
- с изменённым параметром (и площадью )[15]:
Все уравнения, рассмотренные выше, имеют вертикальную ось симметрии (совпадающую с оью ординат) и асимптоту , расположенную снизу от кривой. Но асимптоту можно расположить на графике и сверху, записав уравнение аньезианы в следующей форме:
У всех уравнений, рассмотренные выше, ось симметрии совпадает с осью ординат. У следующих уравнений ось симметрии аньезианы совпадает с осью абсцисс[5]:
- асимптота расположена слева от кривой:
- асимптота расположена справа от кривой:
Частные случаи
Верзиера (локон Аньези) — частный случай аньезианы при со следующим уравнением[3][4][16][9][7][13][17][14][18][19]:
Псевдоверзиера — частный случай аньезианы при со следующим уравнением[20][9]:
Поскольку уравнение верзиеры можно записать в виде
а уравнение псевдоверзиеры в виде
то псевдоверзиера получается удвоением ординат верзиеры, если другими словами, если диаметр образующей окружности верзиеры равен радиусу образующей окружности псевдоверзиеры[8].
Вывод уравнения и геометрическое построение
Получить аньезиану путём гиперболизма базовой окружности радиуса с началом координат на этой окружности и базовой прямой , перпендикулярной диаметру окружности с концом в начале координат[3][21] можно двумя способами:
- исходя из уравнения образующей окружности:
- исходя из преобразования гиперболизма:
Получаем, что преобразование гиперболизма окружности:
- сохраняет ординату
- изменяет абсциссу пропорционально абсциссе и обратно пропорционально ординате с постоянным коэффициентом

Выясним роль образующих окружности и прямой, построив аньезиану геометрически (см. рисунок справа)[2][21]:
- выберем внутри диаметра образующей окружности произвольную точку с ординатой , которая будет также и ординатой аньезианы;
- проведём прямую , которая пересечётся с образующей окружностью в точке на которой будет расположена точка аньезианы;
- проведём образующую прямую ;
- проведём прямую через начало координат, которая пересечётся с образующей прямой в точке ;
- проведём прямую через точку , которая пересечётся с прямой в точке — точке аньезианы.
Так как полюс находится на окружности, то иногда при построении аньезианы вместо окружности используют её точку , диаметрально противоположную полюсу. При этом точка есть основание перпендикуляра, опущенного из точки на произвольную прямую, проходящую через полюс (см. рисунок справа)[6].
Получим уравнение аньезианы в декартовых координатах, исходя из её геометрического построения[17]:
- пусть уравнение прямой есть
- ,
- где — некоторый угловой коэффициент;
- тогда декартовы координаты точки , лежащей на окружности, будут
- а точки —
- наконец, координаты точки получаются
- откуда уравнение аньезианы есть
Другой способ получения уравнения аньезианы в декартовых координатах, исходя из её геометрического построения[19]:
- имеет место пропорция
- имеет место соотношение
- тогда
то есть
Из подобных треугольников 0yP и 0bP' этого геометрического построения также можно получить уравнения преобразования гиперболизма, которое зависит только от образующей прямой и не зависит от образующей кривой[10]:
Образующая окружность есть антигиперболизм аньезианы[10].
Уравнение в других координатных системах
Для перевода уравнения кривой из декартовой в полярную систему координат (и обратно) используют соотношения
поэтому уравнение аньезианы будет следующим[22]:
или
В параметрическом виде уравнение аньезианы на вещественной декартовой плоскости
где
или таким[8]:
где
или таким[18]:
где
или таким[18]:
где
Из декартовых параметрических уравнений
можно получить в параметрическом виде уравнение аньезианы в полярных координатах[23]:
Виды аньезиан
В этом разделе аньезианы определяются уравнением
Точки перегиба и максимум

Вычислим вторую производную функции, задающей аньезиану:
В точке перегиба вторая производная функции меняет знак, то есть необходимое условие точки перегиба — равенство нулю второй производной функции (а заодно и кривизны кривой). Другими словами, точки перегиба суть решение следующего уравнения:
Получаем следующие точки перегиба аньезианы[23][4][5][24][8][14][18] (см. рисунок справа):
лежащие на прямой
Точки экстремума удовлетворяют уравнению
поэтому аньезиана имеет единственный максимум в точке на образующей окружности — вершину[23][4][5].
Пересечение с образующей окружностью

Аньезиана
всегда пересекается с образующей окружностью
в точке вершины и, кроме того, может пересекаться ещё в точках пересечения образующей прямой с образующей окружностью.
Найдём эти две точки. Для этого уравнение аньезианы
подставим в уравнение образующей окружности
получим:
Итак, две искомые точки задаются уравнением
при условии
то есть это точки
В итоге аньезианы по точкам пересечения с образующей окружностью делятся на три вида (см. рисунок справа):
- при имеем три точки пересечения: и
- для пограничной верзиеры с две предыдущие точки пересечения сливаются с «тройной» точкой
- при имеем одну обычную точку пересечения
Примечания
- ↑ 1 2 Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве, 1997, с. 326.
- ↑ 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 4.3. Witch of Agnesi (Fermat, 1666; Agnesi, 1748), с. 90.
- ↑ 1 2 3 4 5 6 7 Ferréol Robert. Witch of Agnesi, 2019.
- ↑ 1 2 3 4 5 6 7 Аньези локон, 1988.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве, 1997, § 2. Атлас кривых. Аньезиана, с. 60.
- ↑ 1 2 3 4 5 Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, с. 73, 215.
- ↑ 1 2 3 4 5 Иванов А. Б. Аньези локон, 1977.
- ↑ 1 2 3 4 5 6 7 8 Савелов А. А. Плоские кривые, 1960, 4. Верзиера, с. 90.
- ↑ 1 2 3 4 5 Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, с. 214.
- ↑ 1 2 3 Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, Класс IV. Гиперболизмы конических сечений, с. 23—24.
- ↑ 1 2 Выгодский М. Я. Справочник по высшей математике, 2006, § 506. Верзьера Аньези, с. 870.
- ↑ Аньези локон, 1970.
- ↑ 1 2 Линия, 1973, с. 467—468.
- ↑ 1 2 3 Выгодский М. Я. Справочник по высшей математике, 2006, § 506. Верзьера Аньези, с. 871.
- ↑ 1 2 Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, с. 215.
- ↑ Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве, 1997, § 2. Атлас кривых. Аньезиана, с. 60, 66.
- ↑ 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 4.3. Witch of Agnesi (Fermat, 1666; Agnesi, 1748), с. 91.
- ↑ 1 2 3 4 Weisstein Eric W. Witch of Agnesi, 2024.
- ↑ 1 2 Савелов А. А. Плоские кривые, 1960, 4. Верзиера, с. 89.
- ↑ Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве, 1997, § 2. Атлас кривых. Аньезиана, с. 60, 177.
- ↑ 1 2 Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, с. 73, 214.
- ↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 5.13. Piriform (De Longchamps, 1886), с. 91.
- ↑ 1 2 3 4 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 4.3. Witch of Agnesi (Fermat, 1666; Agnesi, 1748), с. 92.
- ↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, с. 73, 216.
Источники
- Аньези локон // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1970. Т. 2. Ангола — Барзас. 1970. 632 с. с илл., 32 л. илл., 14 л. карт. С. 115.
- Аньези локон // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 75.
- Выгодский М. Я. Справочник по высшей математике. М.: АСТ: Астрель, 2006. 991 с., ил. ISBN 5-17-012238-1 (ООО «Издательство ACT»). ISBN 5-271-03651-0 (ООО «Издательство Астрель»).
- Иванов А. Б. Аньези локон // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 1 А—Г. М.: «Советская Энциклопедия», 1977. 1152 стб., ил. Стб. 297.
- Линия // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1973. Т. 14. Куна — Ломами. 1973. 624 с. с илл., 32 л. илл., 6 л. карт. С. 466—470.
- Савелов А. А. Плоские кривые. Систематика, свойства, применения. (Справочное руководство) / Под ред. А. П. Нордена. М.: Физматлит, 1960. 293 с., ил.
- Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.
- Шикин Е. В., Франк-Каменецкий М. М. Кривые на плоскости и в пространстве. Справочник с приложенипем дискеты «Плоские кривые». М.: ФАЗИС, 1997. 334 с., ил. ISBN 5-7036-0027-8.
- Ferréol Robert. Witch of Agnesi // ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES Архивная копия от 25 августа 2023 на Wayback Machine
- Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
- Weisstein Eric W. Witch of Agnesi // Wolfram MathWorld Архивная копия от 8 мая 2022 на Wayback Machine