Трапе́ция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Часто в определении трапеции опускают последнее условие. Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся. Четырёхугольник без самопересечений называется простым, часто под термином «четырёхугольник» имеются в виду только простые четырёхугольники.

Практическое построение окружности возможно с помощью циркуля. Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки, в зависимости от подхода, круг может включать или не включать.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.

Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону . В зависимости от типа треугольника высота может содержаться внутри треугольника, совпадать с его стороной или проходить вне треугольника у тупоугольного треугольника.

Проекти́вная пло́скость — двумерное проективное пространство. Важным частным случаем является вещественная проективная плоскость.

Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка пересечения серединных перпендикуляров к сторонам многоугольника.

Дуга́ окру́жности — одна из двух частей (подмножеств) окружности, на которые её разбивают две различные принадлежащие ей точки. Любые две различные точки A и B окружности разбивают её на две части; каждая из этих частей называется дугой.
Угловое ускорение — псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени

Пра́вильный семнадцатиуго́льник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Среди других правильных многоугольников с больши́м простым числом сторон интересен тем, что его можно построить при помощи циркуля и линейки.

Радика́льная ось — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведённых к двум данным окружностям из любой точки  данного геометрического места точек.
данного геометрического места точек.

Хо́рда в планиметрии — отрезок, соединяющий две точки данной кривой.

Задача Наполеона — знаменитая задача построения с помощью циркуля. В этой задаче дана окружность и её центр. Задача состоит в делении окружности на четыре равных дуги с помощью только циркуля. Наполеон был известным любителем математики, но неизвестно, он ли придумал или решил эту задачу. Друг Наполеона итальянский математик Лоренцо Маскерони придумал при геометрических построениях ограничение на использование только циркуля. Но, фактически, задача выше является более простой, чем истинная задача Наполеона, состоящая в нахождении центра окружности с помощью только циркуля. Ниже приведено решение обеих задач и даны доказательства.

В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.

Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.

Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек.

Точка Брокара — одна из двух точек внутри треугольника, возникающих на пересечении отрезков, соединяющих вершины треугольника с соответствующими свободными вершинами треугольников, подобных данному треугольнику и построенных на его сторонах. Считаются замечательными точками треугольника, с их помощью строятся многие объекты геометрии треугольника.

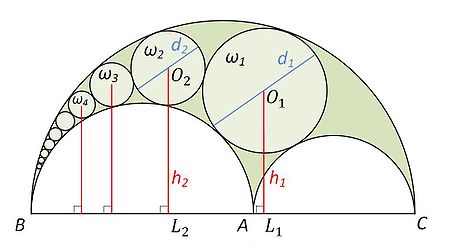
Цепь Паппа Александри́йского — кольцо внутри двух касающихся кругов, заполненных попарно касающимися кругами меньших диаметров. Исследована Паппом Александрийским в III веке н. э.

Модель Пуанкаре в верхней полуплоскости — это верхняя половина плоскости  , обозначаемая ниже как H, вместе с метрикой, которая делает её моделью двумерной гиперболической геометрии.
, обозначаемая ниже как H, вместе с метрикой, которая делает её моделью двумерной гиперболической геометрии.