Асинхронная логика
Асинхро́нная ло́гика — разновидность взаимодействия логических элементов цифровых устройств. Отличается от синхронной тем, что её элементы действуют асинхронно, не подчиняясь глобальному генератору тактовых импульсов.
Описание
Асинхронные схемы управляются двумя сигналами: запрос, который выдается после установки входов и ответ. Относительно пары этих сигналов переходной процесс в асинхронной схеме моделируется элементом задержки, величина которой конечна и заранее неизвестна. В синхронных схемах аномалии динамического поведения (состязания и риски) маскируются с помощью тактового генератора. Для борьбы с аномалиями в асинхронных схемах используется механизм индикации[1], который фиксирует моменты окончания переходных процессов. Готовность сигналов индикации определяется величинами реальных задержек, которые могут изменяться и зависят от условий функционирования схемы (например от температуры). Физически, индикатор окончания переходных процессов в схеме может отсутствовать, тогда его роль выполняют специальные самосинхронные коды[2][3]. Таким образом, по сравнению с синхронными схемами, асинхронные в общем случае, содержат больше логических элементов. Основные преимущества асинхронных схем по сравнению с синхронными это[4][5]:
- устойчивая работа — отсутствие сбоев при любых возможных условиях эксплуатации;
- безопасная работа — остановка в момент появления неисправности любого элемента;
- отсутствие периодов вынужденного простоя в ожидании очередного синхроимпульса.
Синхронные схемы практически любого уровня сложности могут быть реализованы на относительно дешевых ПЛИС. Напротив, строго-самосинхронные схемы предъявляют очень жесткие требования к внутренней структуре ПЛИС[6][7] и практически единственным решением является изготовление ПЛИС на заказ[8][9][10][11]. Однако, стоит отметить попытки реализации асинхронных схем на биполярных ПЗУ[12][13], стандартных PAL (CPLD)[14][15] и FPGA[16][17][18]. Поскольку стандартные FPGA являются синхронными устройствами, на них относительно легко построить схемы с согласованной задержкой[19][20][21] и, сложнее, локально-синхронные (GALS) схемы[22]. В большинстве стандартных FPGA отсутствуют средства реализации арбитров. Один из способов обойти это ограничение представлен в[16]. В статье[17] для реализации строго-самосинхронной схемы предлагается модифицировать FPGA Atmel AT40K с очень мелким размером элементарной ячейки (fine grained)[23],[24]. Реализация С-элемента на двух LUT предложена в[25].
Общие замечания
- При проектировании цифровых устройств принято функционально разделять операционный и управляющий блоки. Операционный блок отвечает за обработку данных (data path[27][28]) и получает команды от управляющего блока (control path). Во многих отношениях такое разделение достаточно условно[4]. Некоторые устройства, например, асинхронная шина, кольцевой интерфейс, арбитр с иерархической структурой и счетчик по модулю n практически не обрабатывают данные, но имеют сложный алгоритм управления. Другие устройства, такие как асинхронный банк регистров или параллельное n-разрядное АЛУ предназначены для интенсивной обработки данных, но управление ими достаточно простое.
- Асинхронные схемы, как и любые схемы с памятью, требуют задания начальных условий. На практике это осуществляется подачей короткого импульса сброса соответствующей полярности на запоминающие элементы. Подробнее см.[29].
- Для правильной работы асинхронных схем необходимо задать поведение внешней среды. Схема, недистрибутивная для одной внешней среды, может оказаться дистрибутивной для другой, последовательной для третьей и неполумодулярной для четвёртой.
Модели и классификация асинхронных схем


Асинхронная схема может рассматриваться как аппаратная реализация параллельной распределенной программы[4]. Для выполнения такой программы во времени обычно необходим какой-либо механизм, в то время как асинхронной схеме этот механизм не нужен. Аналогами операторов и команд в асинхронной схеме являются логические элементы, триггеры или сложные иерархические модули. Роль данных, которыми обмениваются элементы схемы, играют переключения сигналов. Таким образом, все события в схеме уровне упорядочены во времени через причинно-следственные связи. Порядок, установленный разработчиком должен быть сохранен в схеме, то есть фактически сгенерирован, что в конечном счете обеспечивает правильное функционирование. В общем случае, классификация самосинхронных схем довольно сложна и неоднозначна[1][35]. Однако, существуют по крайней мере две достаточно общие модели таких схем с разными предположениями о задержке в элементах, проводах и их соединениях[36][37]:
- Mодель с ограниченной задержкой (модель Хаффмана, Huffman model[38]), в которой предполагается максимальная задержка распространения сигналов в схеме (наихудший случай). Для построения таких схем нужно вводить задержку в цепь обратной связи либо использовать локальную синхронизацию. Таким образом, схемы построенные в соответствии с моделью Хаффмана не являются строго самосинхронными. Пример использования модели Хаффмана — это различные варианты микроконвейеров (micropipelines) с согласованной задержкой[39][40][41][42]. В общем случае нехаффменовские модели — это модели, использующие динамические языки спецификации, для формального анализа или синтеза. Операционные устройства таким образом представить затруднительно.
- Mодель с неограниченной задержкой до точки разветвления (модель Маллера, Muller model[43][44][45]), в которой предполагается, что разница в задержке проводов после разветвления меньше, чем минимальная задержка элемента. Схемы построенные в соответствии с моделью Маллера делятся на несколько классов:
- схемы, не зависящие от скорости (speed-independent, SI circuits);
- полумодулярные или/и дистрибутивные (semi-modular or/and distributive) схемы;
- схемы квазинечувствительные к задержкам (quasi-delay-insensitive, QDI circuits).
Дистрибутивные схемы являются подмножеством полумодулярных, которые в свою очередь, являются подмножеством SI-схем. На практике, класс SI-схем эквивалентен классу QDI. Теория и методы проектирования QDI-схем хорошо развиты и, поэтому, такие схемы наиболее популярны для реализации.
Сложные асинхронные системы нельзя однозначно представить ни моделью Хаффмана ни моделью Маллера. Такие системы могут быть построены как асинхронные конечные автоматы[46][47] или, в очень крупном масштабе, как асинхронные микропроцессорные комплекты[48][49], использующие микропрограммное управление[50][51][52][53]. Подобные комплекты представлены сериями К587[54][55], К588[56] и К1883 (U83x в ГДР)[57]. Обучение проектированию сложных последовательных самосинхронных схем целесообразно начинать с реализации простого одноразрядного процессора MC14500B и объединения таких процессоров в вычислительную структуру[58].
Сильная (И) и слабая (ИЛИ) обусловленность



На интуитивном уровне, обусловленность (причинная-следственная связь, causality) в асинхронных схемах — это зависимость порядка появления выходных сигналов от порядка появления входных. Эта зависимость может быть сильной (И) и слабой (ИЛИ), что соответствует схемам с полной индикацией (full indication) и досрочным получением результата (early evaluation)[61].
Предположим, что некоторое событие имеет две причины: и . И-обусловленность предполагает, что оба события и должны иметь место, прежде чем может произойти событие . Таким образом, в случае И, каждая причина сильно предшествует результату. Аналогом такого поведения в социологии является коллективизм и товарищество. В случае ИЛИ-обусловленности событие может произойти после того, как любое из событий или произошло (здоровый индивидуализм).
Таким образом, в случае ИЛИ, результат появляется если по крайней мере одно событие из набора слабых причин произошло. Чтобы определить как ведет себя событие после того, как обе его слабые причины и произошли, вводятся понятия совместной и несовместной обусловленности [59][60] (соответственно управляемый и неуправляемый индивидуализм). Для двух входных сигналов И-обусловленность моделируется с помощью гистерезисного триггера (Г-триггер, Muller C-element), заданного уравнением . Модель совместной ИЛИ-обусловленности — это элемент «включающее ИЛИ» (inclusive OR[62], EDLINCOR[63]), который использует выход гистерезисного триггера и задается уравнением . Модель полностью несовместной ИЛИ-обусловленности — это схемы, основанные на арбитрах.
Рассмотрим асинхронную схему, в которой есть двухвходовый элемент ИЛИ (двухвходовый элемент И). В фазе гашения на входе элемента ИЛИ установлен код 00, а на входе элемента И — код 11. В рабочей фазе входы один за другим переключатся в 1 (0). Необходимо индицировать оба эти изменения, но в случае ИЛИ-обусловленности процесс будет развиваться по одному входу, а затем второй вход где-то индицируется. Иными словами, процесс начинает ветвиться по первому изменению входа, без ожидания второго, то есть без синхронизации со вторым сигналом. Чем больше таких элементов, тем больше параллельность в схеме. Синхронизация входов возможна, но нежелательна, так как это будет другой процесс с меньшей параллельностью.
Есть два основных метода моделирования ИЛИ-обусловленности на сетях Петри (или STG). Один способ — это уход от явного представления параллельности на уровне переходов сети Петри к уровню так называемой семантики чередования (англ. interleaving semantics) (то есть с выбором на трейсах) — при этом сохраняется 1-безопасность сети Петри. Другой способ — это сохранение явного представления параллельности, но при этом сеть Петри становится не 1-безопасной[60]. Таким образом, ИЛИ-обусловленность описывается либо небезопасной, но устойчивой сетью Петри, либо безопасной, но неустойчивой.
Оба типа обусловленности приводят к полумодулярным схемам. Однако, в случае И-обусловленности эти схемы являются дистрибутивными, а в случае ИЛИ — недистрибутивными. Дистрибутивные схемы могут быть построены из элементов только одного типа (например, И-НЕ или ИЛИ-НЕ), а недистрибутивные требуют использования обоих типов элементов. В случае небезопасной, но устойчивой сети Петри необходимо также бороться с накоплением точек в вершинах OR-causality. Методологии DIMS и NCL, как и любые другие методологии с полной индикацией, имеют все преимущества и недостатки И-обусловленности. Графы сигнальных переходов в своем наиболее простом варианте также реализуют полную индикацию. Диаграммы изменений позволяют моделировать как И-, так и совместную ИЛИ-обусловленность, но не могут напрямую представлять процессы с конфликтами или выбором.
Теорема о соединении полумодулярных схем
Пусть схемы и полумодулярны относительно состояний и соответственно, при этом является выходом инвертора схемы . Разомкнём узел схемы так, что образуются вход и выход . Предположим, что среди состояний в которые могут перейти схемы и из и найдутся такие и в которых значение сигнала на входе и на выходе инвертора совпадает с и с соответственно. Удалим из схемы инвертор так, что образуются вход и выход . Соединим с и с . Можно утверждать, что полученная схема полумодулярна относительно состояния . Интуитивное доказательство теоремы приводится в[1]. Строгое математическое доказательство можно найти в[32]. Важно отметить, что соединение двух схем по теореме требует выполнения двух условий: 1) в одной из схем должен быть инвертор и 2) наличия состояний и . Эти условия выполняются не всегда и, следовательно не любые полумодулярные схемы можно соединять в одну. Обобщение теоремы для более мягких условий приводится в[2]. Частным случаем использования теоремы является повышение быстродействия счетчиков с последовательным переносом[64][65][66][67]. В общем случае, применение теоремы дает качественно новую схему из известных составляющих, например пайплайн на Г-триггерах + статический триггер = асинхронный регистр сдвига.
Двухпроводная линия связи
Простые синхронные схемы можно соединять между собой практически без проблем. Если в полученной сложной схеме отсутствуют критические гонки сигналов, она будет работоспособной. Соединение асинхронных схем гораздо сложнее, в полученной сложной схеме свойство асинхронности может быть утеряно. Результатом этого будет остановка работы или наоборот, генерация пачки импульсов. Если не рассматривать общий провод, то тактовый сигнал на синхронную схему подается по одному проводу. Связать асинхронные схемы можно также по одному проводу[68] но для этого нужно использовать специальный последовательный самосинхронный код. По сравнению с параллельным кодом, это означает более низкое быстродействие и дополнительные расходы оборудования. Для повышения быстродействия можно представлять разделитель (spacer) третьим уровнем сигнала[69][70]. Это позволяет также уменьшить количество проводов (если слоев металлизации не больше двух), но не позволяет переключать линии от разных задатчиков разным исполнителям, то есть не приспособлено для шинных структур. Поскольку в современных технологиях используются 7-14 слоев металлизации, экономить таким образом на проводах не имеет смысла. Два провода позволяют использовать парафазный[71][72][73] протокол связи. Впервые такой подход был использован Д. Е. Маллером для построения строго самосинхронного микроконвейера[72]. Близким к этому способу является Delay Insensitive Minterm Synthesis (DIMS)[74]. Методология Null Convention Logic (NCL)[75] также предназначена для синтеза строго самосинхронных микроконвейеров. В отличие от DIMS, где используются C-элементы, NCL использует многовходовые Г-триггеры, которые называются пороговыми элементами и самосинхронный код М-из-N. В некоторых случаях это позволяет строить более простые схемы. Заметим, что в силу использования Г-триггеров, микроконвейеры DIMS и NCL реализуют только И-обусловленность[76]. Некоторые способы построения микроконвейеров с ИЛИ-обусловленностью рассмотрены в[77][78]. Строго самосинхронные микроконвейерные схемы также могут быть синтезированы при компиляции программ с языков высокого уровня. Следует однако, ожидать, что полученные таким образом схемы будут не оптимальными. Например, сумматор синтезированный в[79] сложнее, чем предложенный в[80].
Асинхронные примитивы
Идея использования примитивов для построения асинхронной схемы аналогична идее конструктора. Детали такого конструктора должны быть по возможности, универсальными[4]. Как правило, они описываются фрагментами устойчивых и безопасных сетeй Петри[45][81]. Наиболее известные асинхронные примитивы это:
Буферный регистр

Впервые предложен в[72] под названием double-line delay (см. также[1][73]) и наиболее известен как weak condition half buffer, WCHB[82].
Ячейка Давида

Названа по фамилии французского инженера René David впервые её предложившего[87][88]. Транзисторная реализация ячейки называется one place buffer, её обобщения рассматриваются в[1][2][3][50][89][90][91].
Схема повторного вхождения

Была впервые предложена в[1] и усовершенствованна в[2]. В последнем варианте рассматривается в[3] и известна как multiple use circuit, D-element, Q-element[94] и S-element[31][95].
Счётный триггер


Также называемый toggle представляет собой делитель частоты на два, в котором обеспечивается завершение переходных процессов. Ранние версии toggle, построенные на элементах с инверсией на входах приведены в[32][101][102][103]. Диаграмма переходов схемы[101] показана на рис. 5.31 в[2]. Задержка входных инверторов во всех этих схемах предполагается нулевой, а индикатором служит либо элемент XOR либо элемент XNOR. Вариант toggle, использующий дуальные логические элементы 1И-2ИЛИ-НЕ и 1ИЛИ-2И-НЕ приводится в[104]. Заметим, что такая реализация известна по крайней мере с 1971 года[105]. Другой вариант toggle, использующий те же элементы и два инвертора предложен в[106] и подробно обсуждается в[107]. Реализация toggle только на элементах И-НЕ (ИЛИ-НЕ)[1][2] иногда называется гарвардский триггер и известна по крайней мере с 1964 года[108]. Компактные статические схемы гарвардского триггера на КМОП транзисторах приведены в[109][110][111], a схема с нагрузочными резисторами — в[112]. Динамическая схема счётного триггера, где предыдущее состояние хранится на емкостях приведена в[113]. Заметим, что большинство счётных триггеров представляют собой последовательностные схемы и поэтому могут быть реализованы только на элементах 2И-НЕ. Существуют, однако, дистрибутивные схемы счётного триггера. Например, в[114] описывается дистрибутивная и очевидно громоздкая схема на четырёх логических и двух С-элементах. Более удачным примером является дистрибутивная схема JK-триггера на 2И-НЕ. Объединив входы J и K, получим счётный триггер.
Последовательное соединение счётных триггеров даёт многоразрядный счетчик, в котором количество срабатываний разряда вдвое меньше, чем количество срабатываний разряда . Чтобы обеспечить в таких счетчиках независимость от задержек обычно используется индикатор завершения переходных процессов во всех разрядах[1]. Схема конвейерного счетчика впервые предожена в[1], запатентована в[115] и перепечатана в[2]. Спецификации и схемы счётчиков с постоянным временем ответа приведены в[104][116][117]. Также, в[104] приводится последовательный счётчик с задержкой распространения переносов. В[118] предложен программируемый счётчик, в котором взаимодействие с внешней средой осуществляется через последний разряд. За счёт этого достигается постоянное время реакции между запросом к счётчику и ответом. Тот ответ, который получен после N запросов является сигналом с частотой поделённой на N.
Методологии проектирования
При проектировании асинхронной схемы необходимо сделать предположение о задержках. Методология самосинхронизации использует гипотезу Маллера относительно задержек в проводах — вся задержка провода приведена к выходу элемента, а разбросом задержек в проводах после разветвления можно пренебречь. В этом случае провода вообще исключаются из рассмотрения. Нарушение гипотезы Маллера приводит к нарушению причинной обусловленности поведения, являющейся логической основой самосинхронизации. Причинная обусловленность требует, чтобы каждое событие в системе являлось причиной, по крайней мере, одного другого события (свойство индицируемости самосинхронных систем[2]). В логических структурах, в отличие от систем передачи, изменение состояния отрезка провода после разветвления может не приводить к переключению логического элемента и, следовательно, не индицироваться. При этом отрезок провода начинает выступать как элемент памяти. Для борьбы с этим, то есть для построения схем, не зависящих от задержек в проводах, необходимо использование либо специальных дисциплин переключения (что сужает класс реализуемых схем[119]), либо использование специальных логических или топологических конструкции, как, например, изохронные разветвления[120][121][122] или разветвления полем (field forks[123][124]), требующих введения новых гипотез или/и приемов проектирования, зависящих от технологии. Эта проблема усугубляется с ростом влияния задержек в проводах и разброса этих задержек. Подавляющее большинство современных методологий проектирования приводят к схемам квази-нечувствительным к задержкам, то есть к схемам где все разветвления являются достаточно короткими и поэтому изохронными[125][126]. Основная задача синтеза асинхронных схем формулируется так[127][128]. Задается спецификация, моделирующая реальный процесс. Затем она анализируется чтобы выявить как полезные, так и аномальные свойства процесса. По результатам анализа исходная спецификация модифицируется с целью предотвращения или/и устранения аномалий. По новой, модифицированной спецификации синтезируется схема, поведение которой совпадает с исходной спецификацией. Краткий список методов анализа и синтеза асинхронных схем на основе моделей событийного типа приведен в[129]. Полный цикл использования этих моделей в современных средствах разработки обсуждается в[130]. Методы синтеза основанные на компиляции программ с языков высокого уровня, а также на теории трейсов рассмотрены в[131][132][133].
Для моделирования поведения логических схем обычно используют устойчивые и безопасные сети Петри[45]. Однако, такие сети не могут моделировать досрочное получение результата, поскольку срабатывание переходов основано на И-обусловленности. Чтобы описать ИЛИ-обусловленность, сеть должна быть небезопасной (более одного маркера в позиции). Когда поведение схемы задано, необходимо преобразовать сеть Петри в диаграмму изменений (диаграмму Маллера), которая является графом с вершинами, обозначенными вектором из устойчивых и возбужденных выходов элементов. Далее следует убедиться, что полученная диаграмма является полумодулярной. Если нет, то это означает, что исходное описание схемы в виде сети Петри является неполным и следует вводить дополнительные события. Если диаграмма изменений полумодулярна, то можно по диаграмме переходов строить функции возбуждения элементов. Далее если эти функции находятся в списке элементов базиса реализации, то все в порядке. Если же нет, то нужно вводить дополнительные переменные, а следовательно, и изменять исходное задание таким образом, чтобы все функции элементов соответствовали функциям базиса реализации. Эта проблема очень сложна и ее формальное решение далеко от оптимальной реализации.
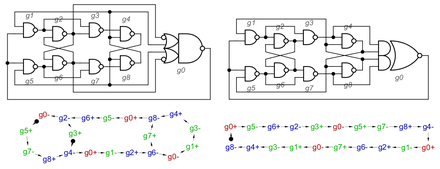
Сигнальные графы


Основаны на сетях Петри, переходы в которых помечены именами сигналов. Впервые были предложены в[140] и описаны более подробно в двух различных подходах в[141] и[142]. Наиболее известны сейчас под названием англ. Signal Transition Graphs, STG[143].
Самый простой класс STG — STG/MG соответствует классу маркированных графов сетей Петри. Это сети Петри, где каждая позиция имеет максимум один входной переход и один выходной переход. В таком графе позиция может иметь только маркеры, удалённые из него через одиночный переход, ведущий от него и переход, однажды разрешённый, может быть запрещен только при фактическом запуске, поэтому не может быть обработана ситуация, где могут происходить А или B, но не оба. Отметим, что графически STG заменяет помеченный переход его меткой, и позиции с одним входом и одним выходом опускаются. Маркеры в этих опущенных положениях просто помещаются на соответствующую дугу. В STG метки переходов содержат не только имя сигнала, но также и определенный тип перехода, нарастающий («+») или спадающий («-»).
Таким образом, когда запускается переход, помеченный , сигнал переключается из 0 в 1; когда запускается переход, помеченный , сигнал переключается из 1 в 0. Переходы на входных сигналах также различаются подчеркиванием. Чтобы создавать схемы по STG, часто требуются выполнения одного или нескольких ограничений: живучести, надежности, постоянства, непротиворечивого назначения состояния, уникального назначения состояния, одноцикловых переходов.
STG живой, если от каждой доступной маркировки каждый переход может быть, в конце концов, запущен.
STG надёжен, если никакая позиция или дуга никогда не могут содержать больше одного маркера.
STG постоянен, если для всех дуг а* → b* (где t* означает переход t+ или t-) имеются другие дуги, гарантирующие, что b* запустится перед противоположным переходом a*.
STG имеет непротиворечивое назначение состояния, если переходы сигнала строго чередуются между + и — (т.e. нельзя возвращаться к тому же состоянию).
STG имеет уникальное назначение состояния, если никакие две различных маркировки STG не имеют идентичных значений для всех сигналов.
STG имеет одноцикловые переходы, если каждое имя сигнала в STG появляется в точно одном нарастающем одном спадающем переходе.
Диаграммы изменений


Диаграммы изменений (англ. Change Diagrams, CD)[144][145][146] подобно STG имеют узлы, маркированные у переходов, и дуги между переходами, которые определяют разрешённые последовательности запуска переходов. CD имеют дуги трех типов: сильного предшествования, слабого предшествования и несвязанного сильного предшествования, а также начальную маркировку, хотя маркеры помещаются в переходы CD вместо позиций. Дуги сильного предшествования подобны дугам в STG и их можно считать дугами AND, так как переход не может запускаться, пока все дуги, указывающие на него, не отмечены маркером. Дуги слабого предшествования являются дугами OR, где переход может запускаться всякий раз, когда какой-либо переход с дугой слабого предшествования к нему отмечен маркером. Заметим, что переход не может иметь сильные и слабые дуги одновременно. Когда дуги сильного или слабого предшествования заставляют переход запускаться, на всех дугах, указывающих на этот переход, маркер удаляется и помещается на все дуги, разрешающие запуск перехода. Поскольку переход с дугами слабого предшествования, ведущими к нему, может запускаться раньше всех дуг, имеющих маркеры, дуги без маркеров имеют открытые циклы, добавленные к ним для индикации «долга» одного маркера. Когда маркер достигает дуги с долгом, маркер и долг взаимно уничтожаются. Таким образом, если маркер приходит на каждую входную дугу слабого предшествования к узлу (если ни одна из этих дуг изначально не отмечена маркерами или открытыми циклами), он будет запускаться только однажды, и может делать это, как только прибудет первый маркер. Наконец, освобождаемые дуги сильного предшествования идентичны дугам сильного предшествования, за исключением того, что после перехода, ведущего к запуску, дуга больше не сдерживает систему (считается удаляемой из CD). Таким образом, эти дуги могут использоваться для связи начального, неповторяющегося набора переходов с бесконечно повторяющимся циклом.
Обусловленные логические сети
Впервые были предложены в[59] под названием англ. Causal Logic Nets, CLN с целью объединить преимущества сетей Петри и диаграмм изменений в представлении различных форм причинно-следственных связей[60].
NCL подход
Сокращение NCL означает Null Convention Logic и указывает на использование разделителя 00. Подход NCL был предложен в[147] для операционных блоков, состоящих преимущественно из самосинхронной комбинационной логики.
Элементы NCL являются частным случаем обобщенного C-элемента, который задан с помощью разложения Шеннона как , где и — это функции установки и сброса. Если эти функции ортогональны, то есть , то и изотонна (positive unate) по . Таким образом, можно исключить, так что . NCL использует пороговые функции установки и сброса, которые имеют не более 4 переменных. В NCL также используются 3 непороговые функции, которые могут быть реализованы несколькими NCL элементами. В дополняющем подходе NCL+ используется разделитель 11. Функция сброса для NCL одна , а функций установки несколько[148][149]. Для NCL+ наоборот, функция установки одна , а функций сброса несколько[150]. Результатом этого является определённая симметрия между КМОП реализациями элементов NCL и NCL+[151],[152]. Однако, такие реализации очень громоздкие, например, элемент TH24 состоит не менее, чем из 26 транзисторов[153]. Построение операционных блоков на NCL называется Flow Computation. Эти блоки представляют собой связанные осцилляторы, которые производят параллельные вычисления. Подобный принцип используется в двумерных распределителях[154], [155][156].
Отметим, что подход подобный NCL, был предложен гораздо раньше в[1]. Этот подход использует либо NCL элементы (Г-триггеры специального типа) либо обычные, многовходовые элементы И-ИЛИ-НЕ[157]. В обоих случаях на элементы подаются парафазные сигналы. На уровне поведения, связь между этим подходом и NCL рассматривается в[158].
Отметим также, что поскольку пороговые функции являются подмножеством монотонных, оба упомянутых подхода могут рассматриваться как развитие последовательностных схем на пороговых элементах[159][160][161][162].
Предположения о длительности задержек
Иногда заданное поведение невозможно реализовать в модели Маллера (задержки элементов неограничены). Как правило, эта проблема связана с заданным базисом реализации. Единственным решением в этом случае является использование предположений о длительности задержек элементов (timing assumptions). Перечислим некоторые признаки таких проблемных поведений:
- Входной сигнал переключается два раза подряд, что приводит к переключению выхода . Другими словами, в поведении имеется фрагмент . Такое поведение не реализуемо в любом базисе. Необходимо предположение о том, что длительности импульса достаточно для (как минимум) двух переключений внутренних сигналов.
- Требование реализовать схему в монотонном однородном базисе, например только на элементах И-НЕ. Заданный интерфейс изменять нельзя. Это означает, что добавлять новые внутренние события перед входными запрещено. В базисе И-НЕ каждая синхронизация происходит только по событиям. Следствием этого является то, что в автономном поведении каждая последовательная ветвь должна начинаться и заканчиваться . Запрет на добавление новых событий перед входными (для не автономных поведений) может привести к нарушению баланса и . Если больше, чем , то схема не реализуема в базисе И-НЕ. Примером может служить реализация С-элемента.
- Использование элементов с полным квитированием (CA) [163],[164]. Пусть входные событие и инициируют альтернативные ветви 1 и 2 соответственно. Если в ветви 2 есть событие , то схема не реализуема на CA-элементах[165].
Основные факты и результаты
- Асинхронные схемы могут рассматриваться как обобщение кольцевого осциллятора. То есть если выходы схемы соединить через модель внешней среды со входами, схема начнёт осциллировать.
- Разделитель (spacer) присутствует только в двухфазных самосинхронныx (СС) кодах. Однофазный СС код — это код с прямыми переходами. Других однофазных СС кодов не существует.
- Реализация логических функций. До сих пор наилучшим универсальным подходом является перекрестная реализация[124][166]. Любая логическая функция от двух и более переменных обладает функциональными состязаниями, с которыми в принципе невозможно бороться. Однако, на сравнимых наборах монотонная (unate) функция свободна от функциональных состязаний. Поэтому удваиваем число входных переменных и заменяем инверсию переменной независимой переменной. Для того чтобы входные наборы стали сравнимыми нужна двухфазная дисциплина, в которой каждый рабочий набор перемежается спейсером (разделителем, состоящим либо из всех нулей, либо из всех единиц). Поскольку спейсер сравним с любым рабочим набором, получаем, что в двухфазной последовательности входов все соседние наборы являются сравнимыми, что необходимо для отсутствия функциональных состязаний. Остаются логические состязания (атрибут реализации). В этом случае помогает перекрестная реализация. Добавляется второй канал реализации, который реализует инверсную функцию (первый канал реализует саму функцию). Причем реализация этого канала должна быть двойственной реализации основного канала. При такой реализации все чистые инверторы в каждом канале заменяются перекрестными связями, так как каждому выходу элемента некоторого яруса соответствует выход элемента в том же ярусе инверсного канала. Эти два выхода образуют пару парафазного кода, что существенно облегчает построение индикатора для логики. В случае использования двухфазной дисциплины со спейсером парафазная реализация в КМОП-технологии не приводит к увеличению числа транзисторов по сравнению с тактируемой однофазной логикой. Это связано с тем, что КМОП-схемы в случае однофазной реализации coдержат прямой и инверсный каналы. Анализ избыточности самосинхронизирующихся кодов позволяет предположить, что для синхронной комбинационной схемы с входами и выходами должна существовать асинхронная схема с входами и выходами. Эта оценка соответствует гипотетической реализации с минимальными дополнительным оборудованием, то есть на практике нижний предел недостижим.
- Реализация индикаторов. Каналы индикации моментов окончания переходных процессов строятся на основе Г-триггеров. Поскольку Г-триггер содержит компоненту И, число его входов ограничено. Таким образом, нужно использовать либо пирамиды из Г-триггеров, либо системы параллельного сжатия, что приводит к затратам оборудования и увеличению задержки в схеме индикации, что может резко снизить быстродействие за счет работы по реальным задержкам. Использование свойства двусторонней проводимости МОП-транзистора позволяет построить схему двухкаскадного индикатора с практически неограниченным числом входов и расходом оборудования 4 транзистора на индицируемый вход[166][167][168].
- Некоторые самосинхронные устройства могут быть реализованы с пренебрежимо малым увеличением оборудования по сравнению с синхронной реализацией. Например счетчики (1974) и память (1986)[169][170][171][172].
- Схемы не зависящие от задержки (DI[173], foam-rubber wrapper[174]), которые состоят из элементов с одним выходом могут содержать только инверторы и С-элементы, что не позволяет строить практические схемы достаточно гибко[119][175]. Невозможно построить полностью независимые от задержек Г-триггер, RS-триггер, Т-триггер[124].
- Любая дистрибутивная схема может быть корректно реализована на двухвходовых элементах И-НЕ (ИЛИ-НЕ) с нагрузочной способностью не больше двух. Любая полумодулярная схема может быть корректно реализована только при совместном использовании этих элементов или при использовании трехвходовых элементов И-ИЛИ-НЕ. Вопрос о корректной реализации полумодулярных схем только на элементах И-НЕ (ИЛИ-НЕ) остается открытым[2][176][177]. На практике однако, минимальный базис не имеет особого смысла ввиду высокой сложности получающихся схем. С ростом значений коэффициентов разветвления и с увеличением функциональных возможностей схемы становятся компактней. В современной КМОП технологии целесообразно использовать элементы сложность которых не превышает 4И-4ИЛИ-НЕ. Не существует полумодулярной схемы из элементов И-НЕ, не чувствительной к задержкам хотя бы в двух ветвях провода, подключенного к выходу элемента, для которого состояния этой схемы живые[178]. Если провод разветвляется, то это функция ИЛИ, поэтому где-то нужно индицировать сигналы в ветвящихся проводах (ИЛИ-обусловленность). Всё вышесказанное справедливо только для парафазной реализации, частным случаем которой является реализация C-элемента только на элементах И-НЕ. Вопрос о реализации однофазных дистрибутивных схем на только элементах И-НЕ остается открытым. Однако, в случае однофазного С-элемента нужны элементы обоих типов. Действительно, чтобы реализовать сильную причинность по нарастающим фронтам, нужен элемент И-НЕ, а по спадающим — ИЛИ-НЕ.
- По одному и тому же проводу запрос можно передавать напряжением, а подтверждение — током. В этом случае для индикации моментов окончания переходных процессов необходимо использовать датчики потребляемого тока КМОП элементов. Однако такие датчики сложны в реализации, а их быстродействие недостаточно. Таким образом, идея комбинированной индикации на практике не ведет к упрощению оборудования. Примером удачного использования этой идеи является метод самосинхронной передачи данных, где каждый бит передается по одному проводу[179]. Для параллельной передачи разрядного двоичного кода этому методу требуется лишь проводов, а его производительность не хуже, чем при передачи данных по двум проводам.
- Индикаторы завершения переходных процессов могут быть построены на основе пороговых схем с несколькими выходами[180].
Библиография
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 А. Г. Астановский, В. И. Варшавский, В. Б. Мараховский и др. Апериодические автоматы. М. Наука, 1976, 423 с. (недоступная ссылка)
- ↑ 1 2 3 4 5 6 7 8 9 10 11 В. И. Варшавский, М. А. Кишиневский, В. Б. Мараховский и др. Автоматное управление асинхронными процессами в ЭВМ и дискретных системах. М.: Наука, 1986. (недоступная ссылка) (V. I. Varshavsky (ed.). Self-Timed Control of Concurrent Processes. (недоступная ссылка))
- ↑ 1 2 3 В. И. Варшавский, В. Б. Мараховский, Л. Я. Розенблюм, А. В. Яковлев, "Асинхронные параллельные процессы и самосинхронные схемы, " Электронная техника. Сер. Упр. кач-вом, стандартизация, метрология, испытания, Вып. 5. № 4, стр. 3-33, 1988.
- ↑ 1 2 3 4 A. V. Yakovlev, A. M. Koelmans, "Petri nets and digital hardware design, " Lectures on Petri Nets II: Applications, vol. 1492, pp 154—236, 1998.
- ↑ C. H. van Berkel, M. B. Josephs, S. M. Nowick, "Applications of asynchronous circuits, " Proceedings of the IEEE, vol. 87, no. 2, pp. 223—233, 1999. Дата обращения: 16 сентября 2015. Архивировано 5 ноября 2015 года.
- ↑ P. S. K. Siegel, Automatic Technology Mapping for Asynchronous Designs. PhD dissertation, Stanford University, 1995, 159 p. Дата обращения: 14 июля 2015. Архивировано 14 июля 2015 года.
- ↑ P. Franklin, D. Winkel, and E. Brunvand, "A comparison of modular self-timed design styles, " Report UUCS-95-025, University of Utah, 1995. Дата обращения: 5 марта 2016. Архивировано 1 августа 2017 года.
- ↑ C. G. Wong, A. J. Martin and P. Thomas, "An architecture for asynchronous FPGAs, " IEEE Int. Conference on Field-Programmable Technology (FPT) 2003, pp. 170—177.
- ↑ D. Shang, F. Xia, A. Yakovlev, "Asynchronous FPGA architecture with distributed control, " IEEE Int. Symposium on Circuits and Systems (ISCAS) 2010, pp. 1436—1439. Дата обращения: 23 июля 2015. Архивировано 24 июля 2015 года.
- ↑ Y. Komatsu, M. Hariyama and M. Kameyama, "Architecture of an Asynchronous FPGA for Handshake-Component-Based Design, " IEICE Transactions on Information and Systems, vol. E96-D, no. 8, 2013, pp. 1632—1644. Дата обращения: 26 июля 2017. Архивировано 31 июля 2017 года.
- ↑ Renesas Electronics. ASIC Product Overview, 2011. Дата обращения: 15 ноября 2019. Архивировано 15 ноября 2019 года.
- ↑ M. Courvoisier, "An asynchronous logic array for the realisation of logic systems with concurrency, " Electronics Letters, vol. 14, no. 4, pp. 119—121, 1978.
- ↑ R. W. Hartenstein, A. Hirschbiel and M. Weber, "Patil array — A Petri net hardware implementation, " CompEuro 1988, pp. 26-33.
- ↑ W. Eisele, G. Eckstein, J. Beister, "VMEbus controller synthesis by communicating asynchronous sequential circuits, " Kaiserslautern University, 1994. Дата обращения: 27 февраля 2016. Архивировано 6 марта 2016 года.
- ↑ L. Lloyd, K. Heron, A. M. Koelmans, A. V. Yakovlev, "Asynchronous microprocessors: From high level model to FPGA implementation, " Journal of Systems Architecture, vol. 45, no. 12-13, pp. 975—1000, 1999. Дата обращения: 27 февраля 2016. Архивировано 12 июля 2012 года.
- ↑ 1 2 S. W. Moore and P. Robinson, "Rapid prototyping of self-timed circuits, " IEEE Int. Conference on Computer Design (ICCD) 1998, pp. 360—365. Дата обращения: 1 марта 2016. Архивировано 8 августа 2017 года.
- ↑ 1 2 K. Meekins, D. Ferguson and M. Basta, "Delay insensitive NCL reconfigurable logic, " IEEE Aerospace Conference 2002, vol. 4, pp. 1961—1966.
- ↑ J. V. Manoranjan and K. S. Stevens, "Burst-mode asynchronous controller implementation on FPG using relative timing, " IEEE Southern Conference on Programmable Logic (SPL) 2014, pp. 1-6. Дата обращения: 31 июля 2017. Архивировано 31 июля 2017 года.
- ↑ R. Payne, "Asynchronous FPGA architectures, " IEE Proceedings, Computers and Digital Techniques, vol. 143, no. 5, pp. 282—286, 1996. Дата обращения: 3 марта 2016. Архивировано 10 марта 2016 года.
- ↑ P. Y. K. Cheung. Are asynchronous ideas useful in FPGAs? This Asynchronous World 87—95 (2016). Дата обращения: 19 февраля 2017. Архивировано 20 февраля 2017 года.
- ↑ Z. Hajduk, «Simple method of asynchronous circuits implementation in commercial FPGAs», Integration the VLSI Journal, vol. 59, 2017, pp. 31-41.
- ↑ V. B. Marakhovsky, A. V. Surkov, "GALA systems of interactive automata," Technical report, 2016. Дата обращения: 13 июня 2016. Архивировано 17 июня 2016 года.
- ↑ M. B. Gokhale, P. S. Graham, Field-Programmable Gate Arrays, § 2.1 in Reconfigurable Computing: Accelerating Computation with Field-Programmable Gate Arrays. Springer, 2005, 238 p. Дата обращения: 17 апреля 2019. Архивировано 17 апреля 2019 года.
- ↑ H. Kaeslin, Field-programmable logic, Ch. 2 in Top-Down Digital VLSI Design: From Architectures to Gate-Level Circuits and FPGAs, pp. 41-61, Elsevier, 2014. Дата обращения: 17 апреля 2019. Архивировано 17 апреля 2019 года.
- ↑ A. Kushnerov, M. Medina and A. Yakovlev, «Towards hazard-free multiplexer based implementation of self-timed circuits Архивная копия от 18 июня 2023 на Wayback Machine,» in IEEE Int. Symposium on Asynchronous Circuits and Systems, 2021.
- ↑ J. C. Kalb, "J-K master-slave flip-flop," Patent US3591856, Jul. 6, 1971. Дата обращения: 29 июля 2019. Архивировано 29 июля 2019 года.
- ↑ D. Sokolov, I. Poliakov and A. Yakovlev, "Asynchronous data path models," IEEE Int. Conference on Application of Concurrency to System Design (ACSD) 2007, pp. 197-210. Дата обращения: 4 августа 2019. Архивировано 17 июня 2018 года.
- ↑ Y. Zhou, C. Shi, Z. Deng and A. Yakovlev, "Synthesis and optimization of asynchronous dual rail encoded circuits based on partial acknowledgement, " IEEE Int. Conference on ASIC 2017, pp. 496-503. Дата обращения: 6 августа 2019. Архивировано 6 августа 2019 года.
- ↑ tutorial:synthesis:initialisation:start - Workcraft. Дата обращения: 8 апреля 2019. Архивировано 8 апреля 2019 года.
- ↑ Tранзисторная схема двух- и трехвходового Г-триггеров известна по крайней мере с 1969 J. J. Gibson, "Logic circuits employing field effect transistors, " Patent US3439185, Apr. 15, 1969. Архивная копия от 30 марта 2019 на Wayback Machine
- ↑ 1 2 C. H. van Berkel, "Beware the isochronic fork, " Report UR 003/91, Philips Research Labs, 1991.
- ↑ 1 2 3 Р. Миллер, Теория переключательных схем, не зависящих от скорости, Гл. 10 в кн. Теория переключательных схем. Том 2: Последовательностные схемы и машины. Наука, 1971, стр. 242—298. Архивная копия от 4 марта 2016 на Wayback Machine (R. E. Miller, "Theory of speed-independent circuits, " Ch. 10 in Switching Theory. Vol. 2: Sequential circuits and machines. Wiley, 1965.)
- ↑ S. J. Silver, J. A. Brzozowski, "True concurrency in models of asynchronous circuit behavior," Formal Methods in System Design, vol. 22, no. 3, pp. 183-203, 2003. Дата обращения: 5 февраля 2016. Архивировано 21 января 2022 года.
- ↑ M. Kishinevsky, A. Kondratyev, A. Taubin, V. Varshavsky, "Analysis and identification of speed-independent circuits on an event model, " Formal Methods in System Design, vol. 4, no. 1, pp. 33-75, 1994. Архивная копия от 11 июня 2018 на Wayback Machine («Анализ и идентификация схем, независимых от скорости, на модели события» Архивная копия от 22 июля 2015 на Wayback Machine)
- ↑ S. H. Unger, "Self-synchronizing circuits and nonfundamental mode operation, " IEEE Transactions on Computers, vol. C-26, no. 3, pp. 278—281, 1977.
- ↑ A. V. Yakovlev, A. M. Koelmans, L. Lavagno, "High level modelling and design of asynchronous interface logic," preprint, 1995. Дата обращения: 23 июля 2015. Архивировано 7 августа 2015 года.
- ↑ J. A. Brzozowski, "Topics in asynchronous circuit theory," Recent Advances in Formal Languages and Applications, vol. 25, pp. 11-42, 2006. Дата обращения: 17 июля 2015. Архивировано 22 июля 2015 года.
- ↑ M. Shams, J. C. Ebergen, M. I. Elmasry, "Asynchronous Circuits, " in Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 1-23, 1999. Дата обращения: 30 января 2016. Архивировано 12 апреля 2012 года.
- ↑ I. E. Sutherland, "Micropipelines, " Communications of the ACM, vol. 32, no. 6, pp. 720—738, 1989. Дата обращения: 27 июля 2015. Архивировано 10 сентября 2016 года.
- ↑ G. Cornetta, J. Cortadella, "Asynchronous pipelined datapaths design techniques. A survey, " pp. 1-31, 1997. Дата обращения: 13 сентября 2015. Архивировано 28 сентября 2015 года.
- ↑ M. Singh, S. M. Nowick, "MOUSETRAP: ultra-high-speed transition-signaling asynchronous pipelines, " International Conference on Computer Design (ICCD) 2001, pp. 9-17. Дата обращения: 27 июля 2015. Архивировано 27 сентября 2015 года.
- ↑ I. Sutherland and S. Fairbanks, "GasP: A minimal FIFO control, " International Symposium on Asynchronous Circuits and Systems (ASYNC) 2001, pp. 46-53. Дата обращения: 29 июля 2015. Архивировано 27 сентября 2015 года.
- ↑ V. Varshavsky, "System time and system timing," Int. Conf. on Semigroups & Algebraic Engineering 1997, pp. 1-25. Дата обращения: 28 января 2016. Архивировано 4 февраля 2016 года.
- ↑ V. Varshavsky, "Time, timing and clock in massively parallel computing systems," Int. Conf. on Massively Parallel Computing Systems 1998, pp. 100-106. Дата обращения: 28 января 2016. Архивировано из оригинала 3 февраля 2016 года.
- ↑ 1 2 3 В. Б. Мараховский, Л. Я. Розенблюм, А. В. Яковлев. Моделирование параллельных процессов. Сети Петри. СПб., Профессиональная литература, 2014, 400с.
- ↑ R. F. Tinder, Engineering Digital Design, 2nd Ed., Academic Press, 2000, 884 p. Дата обращения: 16 ноября 2015. Архивировано 17 ноября 2015 года.
- ↑ R. F. Tinder, Asynchronous Sequential Machine Design and Analysis: A Comprehensive Development of the Design and Analysis of Clock-Independent State Machines and Systems, Morgan & Claypool, 2009, 235 p. Дата обращения: 16 ноября 2015. Архивировано 17 ноября 2015 года.
- ↑ H. W. Lawson, B. Malm, "A flexible asynchronous microprocessor, " BIT Numerical Mathematics, vol. 13, no. 2, pp. 165—176, 1973. Дата обращения: 3 октября 2017. Архивировано 31 января 2018 года.
- ↑ А. А. Васенков и др., "Микропроцессорная вычислительная система, " Авторское свидетельство SU674025, 15/07/1979.
- ↑ 1 2 B. J. Nordmann, B. H. McCormick, "Modular asynchronous control design, " IEEE Transactions on Computers, vol. C-26, no. 3, pp. 196—207, 1977. Дата обращения: 29 сентября 2015. Архивировано 30 сентября 2015 года.
- ↑ H. Lawson, An Asynchronous Approach to Microprogramming. Chapter 3 in Microprogramming and Firmware Engineering Methods. (ed. S. Habib), Wiley, 1988.
- ↑ R. Tinder, R. I. Klaus, "Microprogrammable asynchronous controllers for digital electronic systems, " Patent US5063536, Nov. 5, 1991.
- ↑ R. F. Tinder, R. I. Klaus, J. A. Snodderley, "High-speed microprogrammable asynchronous controller modules, " IEEE Transactions on Computers, vol. 43, no. 10, pp. 1226—1232, 1994.
- ↑ Глава 4.5.3 в биографии Д. И. Юдицкого. Дата обращения: 27 июля 2015. Архивировано 20 июля 2015 года.
- ↑ Серия 587 Архивировано 17 июля 2015 года.
- ↑ С. Т. Хвощ, Н. Н. Варлинский и Е. А. Попов, Микропроцессоры и микроЭВМ в системах автоматического управления. Справочник. Л. Машиностроение, 1987, 638 с.
- ↑ Серия 1883/U830 Архивировано 22 июля 2015 года.
- ↑ W. M. Loucks, M. Snelgrove and S. G. Zaky, "A vector processor based on one-bit microprocessors," IEEE Micro, vol. 2, no. 1, pp. 53-62, 1982. Дата обращения: 23 июля 2017. Архивировано 31 января 2018 года.
- ↑ 1 2 3 A. Yakovlev, M. Kishinevsky, A. Kondratyev and L. Lavagno, "OR causality: modelling and hardware implementation," Int. Conference on Application and Theory of Petri Nets, 1994, pp. 568-587. Дата обращения: 20 апреля 2019. Архивировано 17 июня 2018 года.
- ↑ 1 2 3 4 A. Yakovlev, M. Kishinevsky, A. Kondratyev, L. Lavagno, M. Pietkiewicz-Koutny, "On the models for asynchronous circuit behaviour with OR causality, " Formal Methods in System Design, vol. 9, no. 3, pp. 189—233, 1996. Архивная копия от 5 марта 2016 на Wayback Machine («О моделях для асинхронного режима схемы с причинной связью OR») Архивная копия от 24 июля 2015 на Wayback Machine
- ↑ A. Yakovlev, Asynchronous Design: Quo Vadis? DDECS, Vienna 2010. Дата обращения: 20 июля 2015. Архивировано 9 августа 2017 года.
- ↑ S. E. Elmaghraby, "An algebra for the analysis of generalized activity networks, " Management Science, vol. 10, no. 3, pp.494-514, 1964.
- ↑ D. A. Pucknell, "Event-driven logic (EDL) approach to digital systems representation and related design processes, " IEE Proceedings E, Computers and Digital Techniques, vol. 140, no. 2, pp. 119—126, 1993.
- ↑ В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский и др., "Последовательный счетчик, " Авторское свидетельство SU618853, 05.08.1978.
- ↑ В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский и др., "Последовательный счетчик, " Авторское свидетельство SU706934, 30.12.1979.
- ↑ Б. С. Цирлин, "Последовательный счетчик, " Авторское свидетельство SU1160558, 07.06.1985.
- ↑ Б. С. Цирлин, "Счетчик, " Авторское свидетельство SU1205303, 15.01.1986.
- ↑ K. van Berkel and A. Bink, "Single-track handshake signaling with application to micropipelines and handshake circuits, " IEEE Int. Symposium on Advanced Research in Asynchronous Circuits and Systems, 1996, pp. 122—133.
- ↑ A. S. Wojcik, K. Y. Fang, "On the design of three-valued asynchronous modules, " IEEE Transactions on Computers, vol. C-29, no.10, pp. 889—898, 1980.
- ↑ J. Tse, B. Hill, R. Manohar, "A bit of analysis on self-timed single-bit on-chip links," IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2013, pp. 124—133. Дата обращения: 2 октября 2015. Архивировано 3 октября 2015 года.
- ↑ J. C. Sims and H. J. Gray, "Design criteria for autosynchronous circuits," IEE Eastern Joint Computer Conference (AFIPS) 1958, vol. 14,pp. 94-99. Дата обращения: 3 октября 2015. Архивировано 4 октября 2015 года.
- ↑ 1 2 3 D. E. Muller, "Asynchronous logics and application to information processing," Symposium on the Application of Switching Theory in Space Technology, pp. 289-297, 1963. Дата обращения: 16 сентября 2015. Архивировано 29 сентября 2015 года.
- ↑ 1 2 Г. Цеманек, "Последовательная асинхронная логика, " Mеждународный симпозиум ИФАК Теория конечных и вероятностных автоматов 1962, стр. 232—245. Архивная копия от 5 октября 2015 на Wayback Machine также (H. Zemanek, "Sequentielle asynchrone Logik, " Elektronische Rechenanlagen, vol. 4, no. 6, pp. 248—253, 1962. (недоступная ссылка))
- ↑ J. Sparsø, J. Staunstrup, M. Dantzer-Sørenson, "Design of delay insensitive circuits using multi-ring structures," European Design Automation Conference, 1992, pp. 15-20. Дата обращения: 17 сентября 2015. Архивировано из оригинала 29 сентября 2015 года.
- ↑ A. Kondratyev, K. Lwin, "Design of asynchronous circuits using synchronous CAD tools, " IEEE Design & Test of Computers, vol. 19, no. 4, pp. 107—117, 2002. Архивировано 29 сентября 2015 года.
- ↑ A. Smirnov, A. Taubin, "Synthesizing asynchronous micropipelines with design compiler," Synopsys Users Group Conference, pp. 1-33, 2006. Дата обращения: 21 сентября 2015. Архивировано из оригинала 29 сентября 2015 года.
- ↑ A. Bystrov, D. Sokolov, A. Yakovlev, "Low-latency control structures with slack, " IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2003, pp. 164—173.
- ↑ D. Sokolov, I. Poliakov, A. Yakovlev, "Analysis of static data flow structures," Fundamenta Informaticae, vol. 88, no. 4, pp. 581—610, 2008. Дата обращения: 7 августа 2016. Архивировано 24 августа 2017 года.
- ↑ A. M. Lines, "Pipelined asynchronous circuits," Report CS-TR-95-21, California Institute of Technology, 1998. Дата обращения: 15 марта 2018. Архивировано 14 октября 2017 года.
- ↑ В. И. Варшавский, А. Ю. Кондратьев и В. А. Романовский и Б. С. Цирлин, "Комбинационный сумматор, " Авторское свидетельство SU1596321, 30.09.1990.
- ↑ В. А. Дружинин и С. А. Юдицкий, "Конструирование хорошо сформированных сетей Петри из типовых блоков, " Автоматика и телемеханика, 1992, № 12, 115—121. (V. A. Druzhinin and S. A. Yuditskii, "Construction of well-formed Petri nets from standard subnets, " Automation and Remote Control, vol. 53, no. 12, 1992, pp.1922-1927)
- ↑ M. T. Moreira, J. J. H. Pontes, N. L. V. Calazans, "Tradeoffs between RTO and RTZ in WCHB QDI asynchronous design," IEEE Int. Symposium on Quality Electronic Design (ISQED) 2014, pp. 692—699. Дата обращения: 22 сентября 2015. Архивировано 3 октября 2015 года.
- ↑ В. И. Варшавский, Л. Я. Розенблюм, А. Р. Таубин и Б. С. Цирлин, "Ячейка асинхронного распределителя, " Aвторское свидетельство SU924899 Архивная копия от 21 июня 2023 на Wayback Machine, 30.04.1982.
- ↑ В. И. Варшавский и Б. С. Цирлин, "Асинхронный распределитель, " Aвторское свидетельство SU1022309 Архивная копия от 21 июня 2023 на Wayback Machine, 07.06.1983.
- ↑ В. И. Варшавский, В. Б. Мараховский, Л. Я. Розенблюм, А. Р. Таубин и Б. С. Цирлин, "Асинхронный распределитель, " Aвторское свидетельство SU1026304 Архивная копия от 21 июня 2023 на Wayback Machine, 30.06.1983.
- ↑ В. И. Варшавский, М. А. Кишиневский, В. Б. Мараховский, Л. Я. Розенблюм, А. Р. Таубин и Б. С. Цирлин, "Асинхронный распределитель, " Aвторское свидетельство SU1064461 Архивная копия от 21 июня 2023 на Wayback Machine, 30.12.1983.
- ↑ M. Courvoisier and P. Azema, "Asynchronous sequential machines with request/acknowledge operating mode, " Electronics Letters, vol. 10, no. 1, pp. 8-10, 1974.
- ↑ А. И. Бухштаб, В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский, Л. Я. Розенблюм, Н. А. Стародубцев и Б. С. Цирлин, "Ячейка асинхронного распределителя, " Авторское свидетельство SU718940 Архивная копия от 21 июня 2023 на Wayback Machine, 29.02.1980.
- ↑ V. Varshavsky and V. Marakhovsky, "Hardware support of discrete event coordination," IEE Int. Workshop on Discrete Event Systems (WoDES) 1996, p. 332—339. Дата обращения: 21 сентября 2015. Архивировано 29 сентября 2015 года.
- ↑ A. Yakovlev, F. Burns, A. Bystrov, D. Shang, D. Sokolov, «Is the die cast for the token game?» Int. Conference on Application and Theory of Petri Nets (ICATPN) 2002 Архивировано 2 марта 2016 года.
- ↑ D. Shang, Asynchronous Communication Circuits: Design, Test, and Synthesis, PhD thesis, Newcastle University, 2003, 248 p. Дата обращения: 6 октября 2015. Архивировано 7 октября 2015 года.
- ↑ В. И. Варшавский, В. Б. Мараховский, Б. С. Цирлин и И. В. Яценко, "Кольцевой асинхронный распределитель, " Авторское свидетельство SU1322452, 07.07.1987.
- ↑ С. Г. Арутюнян и В. Ш. Арутюнян, "Кольцевой асинхронный распределитель, " Авторское свидетельство SU1629978, 23.02.1991.
- ↑ A. J. Martin, Programming in VLSI: From communicating processes to delay-insensitive circuits. Report CS-TR-89-1, California Institute of Technology, 1989, 66 p. Дата обращения: 15 сентября 2015. Архивировано 27 сентября 2015 года.
- ↑ M. B. Josephs, A. M. Bailey, "The use of SI-algebra in the design of sequencer circuits," Formal Aspects of Computing, vol. 9, no. 4, pp 395—408, 1997. Дата обращения: 3 октября 2017. Архивировано 5 июня 2018 года.
- ↑ J. W. Foltz, "Binary flip-flop employing insulated gate field effect transistors and suitable for cascaded frequency divider operation," Patent US3679913, Jul. 25, 1972. Дата обращения: 1 августа 2019. Архивировано 1 августа 2019 года.
- ↑ S. Clapper, "Resettable binary flip-flop of the semiconductor type," Patent US3753009, Aug. 14, 1973. Дата обращения: 10 августа 2019. Архивировано 10 августа 2019 года.
- ↑ Ю. Г. Бондаренко, "Триггер со счетным входом," Авторское свидетельство SU425356, 25.04.1974. Дата обращения: 1 июля 2019. Архивировано 1 июля 2019 года.
- ↑ E. A. Vittoz, "Frequency dividing logic structure," Patent US3829714, Aug. 13, 1974. Дата обращения: 1 августа 2019. Архивировано 1 августа 2019 года.
- ↑ Г. С. Брайловский, "Триггер," Авторское свидетельство SU785961, 07.12.1980. Дата обращения: 20 марта 2019. Архивировано 20 марта 2019 года.
- ↑ 1 2 В. И. Горячев, В. М. Климашин, М. А. Комаров и др., "Счетный триггер," Авторское свидетельство SU362351, 13.12.1972. Дата обращения: 26 июня 2019. Архивировано 26 июня 2019 года.
- ↑ В. И. Горячев, Б. М. Мансуров и др., "Однотактный счетный триггер," Авторское свидетельство SU371853, 05.03.1979. Дата обращения: 26 июня 2019. Архивировано 26 июня 2019 года.
- ↑ Н. Г. Коробков и др., "Разряд двоичного последовательного счетчика," Авторское свидетельство SU1014151, 23.04.1983. Дата обращения: 30 июня 2019. Архивировано 30 июня 2019 года.
- ↑ 1 2 3 V. Varshavsky and V. Marakhovsky, "Global synchronization of asynchronous arrays, " IEEE Int. Symposium on Parallel Algorithms/Architecture Synthesis, 1997, pp. 207—215.
- ↑ R. C. Todd, "Logic system," Patent US3609569, Sep. 28, 1971. Дата обращения: 12 апреля 2019. Архивировано 12 апреля 2019 года.
- ↑ N. Starodoubtsev, A. Bystrov and A, Yakovlev, "Semi-modular latch chains for asynchronous circuit design," Int. Workshop on Power and Timing Modeling, Optimization and Simulation (PATMOS) 2000, pp. 168—177. Дата обращения: 20 июля 2017. Архивировано 31 января 2018 года.
- ↑ A. Madalinski, V. Khomenko and A. Yakovlev, "Interactive resolution of encoding conflicts in asynchronous circuits based on STG unfoldings, " Technical Report No. CS-TR-944, Computing Science, University of Newcastle upon Tyne, 2006.
- ↑ G. T. Osborne, "Asynchronous binary counter register stage with flip-flop and gate utilizing plurality of interconnected NOR circuits," Patent US3139540, Jun. 30, 1964. Дата обращения: 28 июля 2019. Архивировано 28 июля 2019 года.
- ↑ В. И. Горячев, Б. М. Мансуров, Я. Д. Мартыненко и Р. Г. Талибов, "Четырехфазовый распределитель импульсов," Авторское свидетельство SU342299, 14.06.1972. Дата обращения: 25 марта 2019. Архивировано 3 апреля 2019 года.
- ↑ В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский и Б. С. Цирлин, "Счетный триггер на КМОП-транзисторах, " Авторское свидетельство SU1398069, 23.05.1988.
- ↑ Б. Цирлин и А. Кушнеров, "Распознавание цифровых схем. Асинхронный счётный триггер," Препринт, 30.10.2019. Дата обращения: 2 ноября 2019. Архивировано 2 ноября 2019 года.
- ↑ Б. С. Цирлин, В. А. Романовский, А. Ю. Кондратьев и Н. А. Голдин, "Счетный триггер, " Авторское свидетельство SU1748230, 15.07.1992.
- ↑ З. Б. Шейдин, А. Г. Габсалямов, И. В. Берг, "Триггер со счетным входом на взаимодополняющих МДП транзисторах," Авторское свидетельство SU1622925, 23.01.1991. Дата обращения: 10 июля 2019. Архивировано 10 июля 2019 года.
- ↑ J. C. Nelson, Speed-independent counting circuits. Report no. 71, Digital Computer Laboratory, University of Illinois at Urbana-Champaign, 1956.
- ↑ В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский и др., "Последовательный счетчик, " Авторское свидетельство SU561298, 05.06.1977.
- ↑ V. I. Varshavsky, V. B. Marakhovsky and V. V. Smolensky, "Designing self-timed devices using the finite automaton model," IEEE Design & Test of Computers, vol. 12, no. 1, pp. 14-23, 1995. Дата обращения: 5 июня 2019. Архивировано из оригинала 5 июня 2019 года.
- ↑ A. V. Yakovlev, A. M. Koelmans, A. Semenov, D. J. Kinniment, "Modelling, analysis and synthesis of asynchronous control circuits using Petri nets, " Integration, the VLSI Journal, vol. 21, no. 3, pp. 143—170, 1996.
- ↑ O. Benafa, D. Sokolov and A. Yakovlev, "Loadable Kessels Counter," IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2018, pp. 102-109. Дата обращения: 7 апреля 2019. Архивировано 7 апреля 2019 года.
- ↑ 1 2 A. J. Martin, "The limitations to delay-insensitivity in asynchronous circuits, " Advanced Research in VLSI, 1990, pp. 263—278.
- ↑ K. van Berkel, F. Huberts, A. Peeters, "Stretching quasi delay insensitivity by means of extended isochronic forks, " Asynchronous Design Methodologies, 1995, pp. 99-106.
- ↑ N. Sretasereekul, Т. Nanya, "Eliminating isochronic-fork constraints in quasi-delay-insensitive circuits, " Asia and South Pacific Design Automation Conference (ASP-DAC) 2001, pp. 437—442.
- ↑ Y. Li, Redressing Timing Issues for Speed-Independent Circuits in Deep Sub-micron Age. PhD thesis, Newcastle University, 2012, 153 p. Дата обращения: 3 октября 2015. Архивировано 4 октября 2015 года.
- ↑ V. I. Varshavsky, Circuits insensitive to delays in transistors and wires. Technical report no. 7, Helsinki University of Technology, 1989, 42 p. Дата обращения: 1 октября 2015. Архивировано 2 октября 2015 года.
- ↑ 1 2 3 M. Kishinevsky, A. Kondratyev, A. Taubin and V. Varshavsky, Review of the State-of-the-Art in Self-timing, Ch. 8 in Concurrent Hardware: The Theory and Practice of Self-Timed Design, Wiley, 1993, 388 p. Дата обращения: 15 ноября 2015. Архивировано 17 ноября 2015 года.
- ↑ S. Hauck, "Asynchronous design methodologies: An overview, " Proceedings of the IEEE, vol. 83, no. 1, pp. 69-93, 1995.(«Методологии асинхронных проектов: краткий обзор» Архивная копия от 22 июля 2015 на Wayback Machine)
- ↑ A. Davis and S. M. Nowick, "An introduction to asynchronous circuit design," Report UUCS-97-013, University of Utah, 1997. Дата обращения: 7 октября 2009. Архивировано 9 июня 2007 года.
- ↑ В. И. Варшавский, В. Б. Мараховский, Л. Я. Розенблюм, А. В. Яковлев, § 4.3 Апериодическая схемотехника, в кн. Искусственный интеллект, Том 3: Программные и аппаратные средства. Под ред. В. Н. Захарова и В. Ф. Хорошевского. М.: Радио и связь, 1990.
- ↑ M. B. Josephs, S. M. Nowick, C. H. van Berkel, "Modeling and design of asynchronous circuits, " Proceedings of the IEEE , vol. 87, no. 2, pp. 234—242, 1999. Дата обращения: 16 сентября 2015. Архивировано из оригинала 6 октября 2016 года.
- ↑ A. Yakovlev, "Use of partial orders for analysis and synthesis of asynchronous circuits," Workshop on unfolding and partial order techniques (UFO) 2007, pp. 12-16. Дата обращения: 15 июля 2015. Архивировано 4 марта 2016 года.
- ↑ D. Sokolov, A. Yakovlev, "Clockless circuits and system synthesis, " IEE Proceedings, Computers and Digital Techniques, vol. 152, no. 3, pp. 298—316, 2005.
- ↑ J. A. Brzozowski, C.-J. H. Seger, "Design of Asynchronous Circuits," Chapter 15 in Asynchronous Circuits. Springer, 1995, 404 p. Дата обращения: 3 октября 2017. Архивировано 31 января 2018 года.
- ↑ R. Puri, Asynchronous Logic Design. Chapter in Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 726—741, 2001. Дата обращения: 4 августа 2015. Архивировано 3 декабря 2015 года.
- ↑ ACiD-WG report on «Design, Automation and Test for Asynchronous Circuits and Systems», edited by D. Edwards and W. Toms, 2004. Архивировано 9 октября 2006 года.
- ↑ Б. С. Цирлин, "Г-триггер, " Авторское свидетельство SU1324106, 15.07.1987.
- ↑ Б. С. Цирлин, "Г-триггер, " Авторское свидетельство SU1162019, 15.06.1985.
- ↑ Б. С. Цирлин, "Г-триггер, " Авторское свидетельство SU1324107, 15.07.1987.
- ↑ Б. С. Цирлин, "Г-триггер, " Авторское свидетельство SU1324108, 15.07.1987.
- ↑ А. И. Бухштаб, В. И. Варшавский, В. Б. Мараховский и др., "Ячейка памяти для буферного регистра, " Авторское свидетельство SU661606 Архивная копия от 19 июня 2023 на Wayback Machine, 05.05.1979.
- ↑ В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1598142 Архивная копия от 20 июня 2023 на Wayback Machine, 07.10.1990.
- ↑ Л. Я. Розенблюм, "Язык сигнальных графов и его использование для моделирования протоколов информационного обмена и апериодических схем," Всесоюзный семинар Моделирование дискретных управляющих и вычислительных систем, стр. 22-24, 1981. Дата обращения: 19 апреля 2019. Архивировано 29 июля 2021 года.
- ↑ L. Ya. Rosenblum and A. V. Yakovlev, "Signal graphs: from self-timed to timed ones," IEEE Int. Workshop on Timed Petri Nets, 1985, pp. 199-207. Дата обращения: 2 сентября 2015. Архивировано 23 октября 2003 года.
- ↑ T.-A. Chu, C. K. C. Leung, and T. S. Wanuga, "A design methodology for concurrent VLSI systems, " IEEE Int. Conference on Computer Design (ICCD) 1985, pp. 407—410.
- ↑ A. V. Yakovlev, "On limitations and extensions of STG model for designing asynchronous control circuits," IEEE Int. Conference on Computer Design (ICCD) 1992, pp. 396—400. Дата обращения: 10 марта 2016. Архивировано 11 марта 2016 года.
- ↑ 1 2 В. И. Варшавский, М. А. Кишиневский, А. Ю. Кондратьев, "Модели для спецификации и анализа процессов в асинхронных схемах, " Изв. АН СССР. Техническая кибернетика, 1988, № 2, стр. 171—190. Архивная копия от 31 января 2018 на Wayback Machine (V. I. Varshavsky, M. A. Kishinevsky, A. Yu. Kondratyev, L. Ya. Rosenblum and A. R. Taubin, "Models for specification and analysis of processes in asynchronous circuits, " Soviet Journal of Computer and Systems Sciences, vol. 26, 1989, pp. 61-76.)
- ↑ M. A. Kishinevsky, A. Yu. Kondratyev, A. R. Taubin, "Specification and analysis of self-timed circuits, " Journal of VLSI Signal Processing, vol. 7, no. 1, pp. 117—135, 1994. Дата обращения: 18 сентября 2015. Архивировано 3 февраля 2016 года.
- ↑ U. Schwiegelshohn, L. Thiele, "Properties of Change Diagrams, " Chap. 4 in Hardware Design and Petri Nets, pp. 77-92, 2000. Дата обращения: 27 января 2016. Архивировано 19 апреля 2016 года.
- ↑ K. M. Fant and S. A. Brandt, "NULL Convention LogicTM: a complete and consistent logic for asynchronous digital circuit synthesis, " IEEE Int. Conference on Application Specific Systems, Architectures and Processors (ASAP) 1996, pp. 261—273.
- ↑ M. Ligthart, K. Fant, R. Smith, A. Taubin, and A. Kondratyev, "Asynchronous design using commercial HDL synthesis tools, " in IEEE Int. Symp. on Async. Circuits and Systems (ASYNC), 2000, pp. 114—125.
- ↑ C. Jeong and S. M. Nowick, "Technology mapping for robust asynchronous threshold networks," ACM/IEEE Int. Workshop on Timing Issues (TAU) 2006, pp. 22-27. Дата обращения: 11 мая 2019. Архивировано 29 августа 2017 года.
- ↑ M. T. Moreira, C. H. M. Oliveira, R. C. Porto and N. L. V. Calazans, "NCL+: Return-to-one Null Convention Logic," IEEE Int. Midwest Symposium on Circuits and Systems (MWSCAS) 2013, pp. 836-839. Дата обращения: 22 сентября 2015. Архивировано 6 февраля 2016 года.
- ↑ G. E. Sobelman and D. Parker, «Programmable gate array Архивная копия от 18 июня 2023 на Wayback Machine». Patent US5986466, 16 Nov. 1999.
- ↑ A. Kondratyev, «Multi-rail asynchronous flow with completion detection and system and method for designing the same Архивная копия от 18 июня 2023 на Wayback Machine,» Patent US6526542, Feb. 25, 2003.
- ↑ A. Kushnerov and S. Bystrov, «On minimal realization and behavior of NCL gates Архивная копия от 18 июня 2023 на Wayback Machine,» Preprint, 2022, DOI:10.13140/RG.2.2.31525.47847
- ↑ А. Н. Фойда, «Сдвиговый регистр Архивная копия от 18 июня 2023 на Wayback Machine,» Авторское свидетельство SU643974, 25.01.1979.
- ↑ Б. С. Цирлин, "Асинхронный последовательный регистр, " Авторское свидетельство SU1805501, 30.03.1993.
- ↑ G. Gopalakrishnan, «Some unusual micropipeline circuits Архивная копия от 18 июня 2023 на Wayback Machine,» Report UUCS-93-015, University of Utah, pp. 1-16, 1993.
- ↑ А. И. Бухштаб, В. И. Варшавский, В. Б. Мараховский и др., «Универсальный логический модуль Архивная копия от 18 июня 2023 на Wayback Machine,» Авторское свидетельство SU561182, 05.06.1977.]
- ↑ A. Kushnerov and S. Bystrov, «Signal transition graphs for asynchronous data path circuits Архивная копия от 18 июня 2023 на Wayback Machine,» Modeling and Analysis of Information Systems, vol. 30, no. 2, pp. 170—186, 2023. DOI: 10.18255/1818-1015-2023-2-170-186
- ↑ R. O. Winder, «Flip-flop employing three interconnected majority-minority logic gates Архивная копия от 18 июня 2023 на Wayback Machine,» Patent US3403267, Sep. 24, 1968.
- ↑ R. O. Winder, "Threshold gate counters," Patent US3519941, Jul. 7, 1970. Дата обращения: 26 июля 2019. Архивировано 26 июля 2019 года.
- ↑ В. Н. Тазиян, «Счетный триггер Архивная копия от 18 июня 2023 на Wayback Machine,» Авторское свидетельство SU372697, 01.03.1973.
- ↑ С. О. Мкртчян, «I-K-триггер Архивная копия от 26 июля 2019 на Wayback Machine,» Авторское свидетельство SU421111 25.03.1974.
- ↑ B. C. Kuszmaul, "A glitch in the theory of delay-insensitive circuits, " ACM Int. Workshop on Timing Issues in the Specification and Synthesis of Digital Systems (TAU), 1990. Дата обращения: 23 июля 2021. Архивировано 23 июля 2021 года.
- ↑ N. Starodoubtsev and A. Yakovlev, "Isochronic fork-free asynchronous circuits," UK Asynchronous Forum 2000, pp. 55-60. Дата обращения: 15 мая 2022. Архивировано 15 мая 2022 года.
- ↑ N. Starodoubtsev, S. Bystrov and A, Yakovlev, "Monotonic circuits with complete acknowledgement," IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2003, pp. 98-108. Дата обращения: 20 июля 2017. Архивировано 31 января 2018 года.
- ↑ 1 2 В. Б. Мараховский, Логическое проектирование асинхронных схем. Слайды по курсу, Кафедра АиВТ СПбГПУ. Дата обращения: 22 августа 2015. Архивировано 4 марта 2016 года.
- ↑ В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко, Б. С. Цирлин, "Г-триггер, " Авторское свидетельство SU1411934, 23/07/1988.
- ↑ В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский, Б. С. Цирлин, "Г-триггер, " Авторское свидетельство SU1443137, 07/12/1988.
- ↑ В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский и Б. С. Цирлин, "Запоминающее устройство на КМОП-транзисторах, " Авторское свидетельство SU1365129, 07.01.1988.
- ↑ Б. С. Цирлин, А. Ю. Кондратьев, Н. А. Голдин и В. А. Романовский, "Оперативное запоминающее устройство, " Авторское свидетельство SU1589324, 30.08.1990.
- ↑ U. Cummings and A. Lines, "Asynchronous static random access memory," Patent US7161828, Jan. 9, 2007. Дата обращения: 23 октября 2022. Архивировано 23 октября 2022 года.
- ↑ A. Baz, D. Shang and A. Yakovlev, "Self-timed SRAM for energy harvesting systems," Journal of Low Power Electronics, vol. 7, no. 2, 2011, pp.274-284. Дата обращения: 28 июля 2017. Архивировано 28 июля 2017 года.
- ↑ J. T. Udding, Classification and Composition of Delay-Insensitive Circuits, PhD thesis, Eindhoven University of Technology, 1984.
- ↑ C.E. Molnar, T.P. Fang, and F.U. Rosenberger, "Synthesis of delay-insensitive modules, " Chapel Hill Conference on VLSI, 1985.
- ↑ H. Saito, A. Kondratyev, J. Cortadella, L. Lavagno, A. Yakovlev, «What is the cost of delay insensitivity?» IEEE/ACM Int. Conference on Computer-Aided Design 1999, pp. 316—323. Дата обращения: 27 января 2016. Архивировано 1 февраля 2016 года.
- ↑ Б. С. Цирлин, "Минимальный базис реализации последовательных схем, " Изв. АН СССР, Техническая кибернетика, № 2, 1985, стр. 91-97. Архивная копия от 31 января 2018 на Wayback Machine (B. S. Tsirlin, "Minimal Basis for Realization of Sequential Circuits, " Soviet Journal of Computer and Systems Sciences, vol. 23, 1985, pp. 26-31.)
- ↑ В. И. Варшавский, М. А. Кишиневский, В. Б. Мараховский, Л. Я. Розенблюм, "Функциональная полнота в классе полумодулярных схем, " Известия АН СССР, Техническая кибернетика, № 3, 1985, стр. 103—114. (V. I. Varshavskiy, M. A. Kishinevskiy, V. B. Marakhovskiy and L. Ya. Rozenblyum, "Functional Completeness in the Class of Semimodular Circuits, " Soviet Journal of Computer and Systems Sciences, vol. 23, № 6, 1985, pp. 70-80. Архивная копия от 31 января 2018 на Wayback Machine)
- ↑ Б. С. Цирлин, "Обзор эквивалентных проблем реализации схем в базисе И-НЕ, не зависящих от скорости, " Изв. АН СССР, Техническая кибернетика, № 2, 1986, стр. 159—171. Архивная копия от 29 июля 2017 на Wayback Machine (B. S. Tsirlin, "A survey of equivalent problems of realizing circuits in the AND-NOT basis that are speed-independent, " Soviet Journal of Computer and Systems Sciences, vol. 24, 1986, pp. 58-69.)
- ↑ V. I. Varshavsky, V. B. Marakhovsky, R. A. Lashevsky, "Self-timed data transmission in massively parallel computing systems, " Integrated Computer-Aided Engineering, vol. 4, no. 1, pp. 47-65, 1997.
- ↑ S. J. Piestrak, «Membership test logic for delay-insensitive codes», IEEE Int. Symposium on Advanced Research in Asynchronous Circuits and Systems (ASYNC) 1998, pp. 194—204. Дата обращения: 3 февраля 2017. Архивировано 31 января 2018 года.
Дополнительная литература
Отчёты и книги
- D. E. Muller, Theory of asynchronous circuits. Report no. 66, Digital Computer Laboratory, University of Illinois at Urbana-Champaign, 1955.
- J. C. Nelson, Speed-independent counting circuits. Report no. 71, Digital Computer Laboratory, University of Illinois at Urbana-Champaign, 1956.
- D. E. Muller, W. S. Bartky, A theory of asynchronous circuits I. Report no. 75, Digital Computer Laboratory, University of Illinois at Urbana-Champaign, 1956.
- D. E. Muller, W. S. Bartky, A theory of asynchronous circuits II. Report no. 78, Digital Computer Laboratory, University of Illinois at Urbana-Champaign, 1957.
- J. H. Shelly, The decision and synthesis problems in semimodular switching theory, PhD thesis, University of Illinois at Urbana-Champaign, 1959, 93 p.
- W. S. Bartky, A theory of asynchronous circuits III. Report no. 96, Digital Computer Laboratory, University of Illinois at Urbana-Champaign, 1960.
- A. M. Bush, A method for sensing the completion of operations in speed-independent asynchronous computer circuits. MSc thesis, Georgia Institute of Technology, 1961, 67 p.
- R. E. Swartwout, Further studies in speed-independent logic for a control. PhD thesis, University of Illinois at Urbana-Champaign, 1962, 104p.
- А. Н. Юрасов, Теория построения релейных схем. Госэнергоиздат, 1962, 119с.
- W. D. Frazer, A switching theory for bilateral nets of threshold elements. PhD thesis, University of Illinois at Urbana-Champaign, 1963, 69 p.
- K. E. Batcher, Speed-independent NOR realizations. PhD thesis, University of Illinois at Urbana-Champaign, 1964, 44 p.
- Р. Миллер, Теория переключательных схем, не зависящих от скорости, Гл. 10 в кн. Теория переключательных схем. Том 2: Последовательностные схемы и машины. Наука, 1971, с.242—298.
- P. S. Thiagarajan, Algebraic models for asynchronous control structures. PhD thesis, Rice University, 1972, 133p.
- А. Г. Астановский, В. И. Варшавский, В. Б. Мараховский и др. Апериодические автоматы. М. Наука, 1976, 423 с.
- Б. С. Цирлин. Вопросы синтеза апериодических схем. Диссертация к.т. н. Ленингр. ин-т авиац. приборостроения, 1976, 215 с.
- С. Ангер, Схемы вырабатывающие сигналы завершения, § 6.1 в кн. Асинхронные последовательностные схемы, Наука, 1977, 400с.
- А. Фридман и П. Менон, Логические элементы с неограниченными задержками, § 4.9 в кн. Теория и проектирование переключательных схем, М. Мир, 1978, стр. 275—282.
- C. L. Seitz, "System timing, " Ch. 7 in Introduction to VLSI Systems, C. A Mead and L. A Conway, pp. 218—262, Addison-Wesley, 1980.
- Б. С. Цирлин, Алгебра и анализ асинхронных логических схем. Препринт, Ин-т соц.-экон. пробл. АН СССР, 1981, 39 с. (недоступная ссылка)
- Ю. В. Мамруков, Анализ апериодических схем и асинхронных процессов. Диссертация к.т. н. ЛЭТИ, 1984, 219 с. (недоступная ссылка)
- Н. А. Стародубцев, Синтез схем управления параллельных вычислительных систем. Л. Наука, 1984, 191 с.
- В. И. Варшавский, М. А. Кишиневский, В. Б. Мараховский и др. Автоматное управление асинхронными процессами в ЭВМ и дискретных системах. М.: Наука, 1986. Translated to English as Self-Timed Control of Concurrent Processes: The Design of Aperiodic Logical Circuits in Computers and Discrete Systems.
- V. I. Varshavsky (ed.), Hardware Support of Parallel Asynchronous Processes. Research report, Helsinki University of Technology, 1987, 235 p.
- T.-A. Chu, Synthesis of Self-Timed VLSI Circuits from Graph-Theoretic Specifications. Ph.D. thesis, Massachusetts Institute of Technology, 1987, 189 p.
- L. Hluchý, B. Cirlin, B. Gaži, K. Košuk, T. Pažurová, Rýchly sériový asynchrónny kanál (Fast serial asynchronous channel). Report. Institute of Technical Cybernetics SAS, Bratislava, 1988.
- V. I. Varshavsky, Circuits insensitive to delays in transistors and wires. Technical report no. 7, Helsinki University of Technology, 1989, 42 p.
- G. Gopalakrishnan and P. Jain, Some recent asynchronous system design methodologies. Technical Report UUCS-TR-90-016. Dept. of Computer Science, University of Utah, 1990, 16 p.
- L. Lavagno, Synthesis and Testing of Bounded Wire Delay Asynchronous Circuits from Signal Transition Graphs. PhD thesis, University of California at Berkeley, 1992, 306 p.
- О. А. Изосимов. Методы синтеза и динамического анализа самосинхронных КМДП СБИС. Диссертация к.т. н., МИФИ, 1993, 165 с.
- M. Kishinevsky, A. Kondratyev, A. Taubin and V. Varshavsky, Concurrent Hardware: The Theory and Practice of Self-Timed Design, Wiley, 1993, 388 p.
- K. van Berkel, Handshake Circuits: An Asynchronous Architecture for VLSI Programming. Cambridge, 225 p.
- P. A. Beerel, CAD tools for the synthesis, verification, and testability of robust asynchronous circuits. PhD thesis, Stanford University, 1994.
- M. Kishinevsky, L. Lavagno and P. Vanbekbergen, The Systematic Design of Asynchronous Circuits. Tutorial, Int. Conference on Computer-Aided Design (ICCAD) 1995, 219p.
- J. A. Brzozowski, C.-J. H. Seger, Asynchronous Circuits. Springer, 1995, 404 p.
- S. S. Appleton, Performance-Directed Design of Asynchronous VLSI Systems. PhD thesis, University of Adelaide, 1997, 285p.
- S. V. Morton, Fast Asynchronous VSLI Circuit Design Techniques and Their Application to Microprocessor Design. PhD thesis, University of Adelaide, 1997, 224p.
- S. P. Wilcox, Synthesis of asynchronous circuits. PhD dissertation, University of Cambridge, 1999, 250 p.
- C. J. Myers, Asynchronous Circuit Design. Wiley, 2001, 392 p.
- J. Sparsø, "Asynchronous circuit design — a tutorial, " Chapters 1-8 in Principles of asynchronous circuit design: A systems perspective. Kluwer, 2001, 152p. Translated to Russian as «Проектирование асинхронных схем — вводное руководство»
- J. Cortadella, M. Kishinevsky, A. Kondratyev, L. Lavagno and A. Yakovlev, Logic Synthesis for Asynchronous Controllers and Interfaces. Springer, 2002, 272 p.
- A. Yakovlev, Theory and Practice of Using Models of Concurrency in Hardware Design. DSc. thesis based on publications, University of Newcastle upon Tyne, 2005, 27 p.
- K. M. Fant, Logically Determined Design: Clockless System Design with NULL Convention Logic. Wiley, 2005, 292 p.
- W. B. Toms, Synthesis of Quasi-Delay-Insensitive Datapath Circuits. PhD thesis, University of Manchester, 2006, 237 p.
- P. A. Beerel, R. O. Ozdag, M. Ferretti, A Designer’s Guide to Asynchronous VLSI. Cambridge, 2010, 339 p.
- Л. П. Плеханов, Основы самосинхронных электронных схем. Бином, 2013, 208 с.
- В. Б. Мараховский, Л. Я. Розенблюм, А. В. Яковлев. Моделирование параллельных процессов. Сети Петри. СПб., Профессиональная литература, 2014, 400с.
- D. Furey, Delay Insensitive Circuits. Plumstead, 2019, 652 p.
Статьи
- В. А. Розенберг, "Некоторые свойства релейного набора, " Автоматика и телемеханика, № 1, с.37-48, 1939.
- В. А. Розенберг, "Задача о блокировке и преобразование контактных групп, " Автоматика и телемеханика, № 1, с.47-54, 1940.
- А. Н. Юрасов, "Аналитический синтез многотактных схем по формулам включения, " в сб. Логические исследования, под ред. Кольман Э. Я. и др. АН СССР, с.442-449, 1959.
- D. E. Muller and W. S. Bartky, "A theory of asynchronous circuits, " Int. Symposium on the Switching Theory in Harvard University, pp. 204—243, 1959.
- R. S. Ledley, J. B. Wilson, "Boolean matrices applied to sequential circuit theory and threshold logics, " IEEE Transactions on Communication and Electronics, vol. 83, no. 75, pp. 768—773, 1964.
- H. Eriksson, P. E. Danielsson, "Two problems on Boolean memories, " IEEE Transactions on Electronic Computers, vol. EC-16, no. 3, pp. 364—365, 1967.
- G. G. Langdon, "Analysis of asynchronous circuits under different delay assumptions, " IEEE Transactions on Computers, vol. C-17, no. 12, pp. 1131—1143, 1968.
- I. Kimura, "Extensions of asynchronous circuits and the delay problem I. Good extensions and the delay problem of the first kind, " Journal of Computer and System Sciences, vol. 2, no. 3, pp. 251—287, 1968.
- I. Kimura, "Extensions of asynchronous circuits and the delay problem. Part II: Spike-free extensions and the delay problem of the second kind, " Journal of Computer and System Sciences, vol. 5, no. 2, pp. 129—162, 1971.
- I. Kimura, "Space-continuous time-semicontinuous theory of speed-independent asynchronous circuits, " Information and Control, vol. 22, no. 4, pp. 373—393, 1973.
- D. Bjørner, "A flow-mode, self-steering, cellular multiplier-summation processor," BIT Numerical Mathematics, vol. 10, no. 2, pp. 125—144, 1970.
- R. M. Keller, "Towards a theory of universal speed-independent modules, " IEEE Transactions on Computers, vol. C-23, no. 1, pp. 21-33, 1974.
- В. И. Варшавский, Л. Я. Розенблюм, Η. Α. Стародубцев, "О среднем времени формирования сигналов переноса в апериодических схемах счетчика и сумматора," Автоматика и вычислительная техника, 1975, №3, стр.88-96.
- P. Corsini, G. Frosini, "Interconnecting asynchronous control networks," Information and Control, vol. 38, no. 3, pp. 343—366, 1978.
- В. Варшавский, Е. Воробьев, В. Ломунов, "Формальный подход к анализу логического уровня," Изв. АН Эстонской СССР. Физика, Математика, 1981, Том 30, №4, стр.381–387.
- В. И. Варшавский, М. А. Кишиневский, А. Р. Таубин и Б. С. Цирлин, "Анализ асинхронных логических схем. II. Достижимость рабочих состояний и влияние задержек в проводах," Изв. АН СССР. Техническая кибернетика, 1982, №4, стр.84-97.
- М. А. Кишиневский, А. Р. Таубин и Б. С. Цирлин, "Сети Петри и анализ переключательных схем," Кибернетика, 1982, №4, стр.114-117.
- Б. С. Цирлин, "Базисы реализации последовательных схем," Изв. АН СССР, Техническая кибернетика, 1984, №1, стр.128-134.
- Б. С. Цирлин, "Изоморфные алгебры асинхронных логических схем," Кибернетика, 1984, №2, стр.112-113.
- Б. С. Цирлин, "Минимальный базис реализации последовательных схем," Изв. АН СССР, Техническая кибернетика, № 2, 1985, стр. 91-97.
- Л. Я. Розенблюм и Б. С. Цирлин, "Конвейеризация сетей Петри," Программирование, №1, 1985, стр.9-15.
- Н. А. Стародубцев, "Асинхронные процессы и антитонные управляющие схемы. I. Язык описания, " Изв. АН СССР. Техническая кибернетика, 1985, № 1, стр.10-19.
- Н. А. Стародубцев, "Асинхронные процессы и антитонные управляющие схемы. II. Основные свойства, " Изв. АН СССР. Техническая кибернетика, 1985, № 4, стр.115-122.
- Н. А. Стародубцев, "Асинхронные процессы и антитонные управляющие схемы. III. Реализация, " Изв. АН СССР. Техническая кибернетика, 1985, № 6, стр.83-92.
- P. F. Lister, A. M. Alhelwani, "Design methodology for self-timed VLSI systems, " IEE Proceedings in Computers and Digital Techniques, vol. E132, no. 1, pp. 25-32, 1985.
- L. Nowak, "SAMP: A general purpose processor based on a self-timed VLIW structure, " ACM Computer Architecture News, vol. 15, no. 4, 1987, pp. 32-39.
- R. Melhem, "Verification of a class of self-timed computational networks, " BIT Computer Science, vol. 27, no. 4, pp. 480—500, 1987.
- Л. Я. Розенблюм, "Сети Петри, " Изв. АН СССР. Техническая кибернетика, 1988, № 5, стр. 12-40.
- S. I. Benjamin, Dataflow: Overview and simulation. MSc thesis, Rochester Institute of Technology, 1988, 106 p.
- L. Rosenblum, A. Yakovlev, and V. Yakovlev, A look at concurrency semantics through «lattice glasses», Bulletin of the European Association for Theoretical Computer Science (EATCS), vol. 37, pp. 175—180, 1989.
- A. J. McAuley, "Four state asynchronous architectures, " IEEE Transactions on Computers, vol. 41, no. 2, pp. 129—142, 1992.
- M. Kishinevsky, J. Staunstrup, "Characterizing speed-independence of high-level designs, " IEEE Int. Symposium on Advanced Research in Asynchronous Circuits and Systems, pp. 44-53, 1994.
- V. I. Varshavsky, "Logic design and quantum challenge, " IEEE Int. Workshop on Physics and Computer Modeling of Devices Based on Low-Dimensional Structures, 1995, pp. 134—146. Translated to Russian as "Логическое проектирование и квантовый вызов, " Информационно-управляющие системы, № 4, 2005, стр. 22-32.
- S. Moore, P. Robinson, and S. Wilcox, "Rotary pipeline processors, " IEE Proceedings, Computers and Digital Techniques, vol. 143, no. 5, pp. 259—265, 1996.
- W. H. F. J. Korver, I. M. Nedelchev, "Asynchronous implementation of the SCPP-A counterflow pipeline processor, " IEE Proceedings on Computers and Digital Techniques, vol. 143, no. 5, pp. 287—294, 1996.
- F. Burns, D. Shang, A. Koelmans, A. Yakovlev, "An asynchronous synthesis toolset using Verilog, " IEEE Design, Automation and Test in Europe Conference (DATE) 2004, vol. 1, pp. 724—725.
- D. H. Linder and J. C. Harden, "Phased logic: supporting the synchronous design paradigm with delay-insensitive circuitry, " IEEE Transactions on Computers, vol. 45, no. 9, pp. 1031—1044, 1996.
- J. O’Leary, G. Brown, "Synchronous emulation of asynchronous circuits, " IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 16, no. 2, pp. 205—209, 1997.
- M. H. Sawasaki, C. Ykman-Couvreur and B. Lin, "Externally hazard-free implementations of asynchronous control circuits, " IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 16, no. 8, pp. 835—848, 1997.
- J. Cortadella, M. Kishinevsky, Tutorial: Synthesis of control circuits from STG specifications. Summer school. Lyngby 1997
- N. A. Starodoubtsev, Asynchronous negative logic synthesis from STG-like specifications. ACiD-WG workshop. St. Petersburg, 1998.
- C. Piguet, J. Zahnd, "STG-based synthesis of speed-independent CMOS cells, " Workshop on Exploitation of STG-based Design Technology, 1998, pp. 1-23.
- L. A. Plana and S. H. Unger, "Pulse-mode macromodular systems, " IEEE Int. Conference on Computer Design (ICCD) 1998, pp. 348—353.
- A. Kondratyev, M. Kishinevsky and A. Yakovlev, "Hazard-free implementation of speed-independent circuits, " IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 17, no. 9, pp. 749—771, 1998.
- A. Kondratyev, J. Cortadella, M. Kishinevsky, L. Lavagno and A. Yakovlev, "Logic decomposition of speed-independent circuits, " Proceedings of the IEEE, vol. 87, no. 2, pp. 347—362, 1999.
- M. J. Liebelt and C.-C. Lim, "A method for determining whether asynchronous circuits are self-checking, " IEEE Int. Asian Test Symposium (ATS) 2000, pp. 472—477.
- I. Blunno, and L. Lavagno, «Deriving signal transition graphs from behavioral Verilog HDL,» Hardware Design and Petri Nets, Springer, 2000, pp. 151—170.
- J. Carmona, J. Cortadella, E. Pastor, "A structural encoding technique for the synthesis of asynchronous circuits, " IEEE Int. Conference on Application of Concurrency to System Design, 2001, pp. 157—166.
- M. Neidengard, B. A. Minch, "Hysteretic threshold logic and quasi-delay insensitive asynchronous design, " IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 49, no. 10, pp. 1423—1428, 2002.
- A. Yakovlev, Advanced Course: Hardware and Petri nets. Eichstätt, 2003.
- A. V. Yakovlev, Clockless computing or learning how to play «soft time» in «hard space» Известия СПбГЭТУ «ЛЭТИ». Сер. «Информатика, управление и компьютерные технологии», Вып. 1, стр. 55-64, 2003.
- A. Yakovlev , A. Bystrov , D. Sokolov , V. Varshavsky and V. Marakhovsky, "Phase-difference based logic: Principle and applications, " ACiD-WG 2004
- D. Shang, F. Burns, A. Koelmans, A. Yakovlev and F. Xia, "Asynchronous system synthesis based on direct mapping using VHDL and Petri nets, " IEE Proceedings on Computers and Digital Techniques, vol. 151, no. 3, pp. 209—220, May 2004.
- D. A. Edwards, W. B. Toms, "The status of asynchronous design in industry, " Report IST-1999-29119 on Information Society Technologies (IST) Programme, 2004
- R. R. Redziejowski, "Asynchronous circuits, communicating processes, and Muller automaton, " Fundamenta Informaticae, vol. 61, no. 1, pp. 47-59, 2004.
- L. Necchi, L. Lavagno, D. Pandini and L. Vanzago, "An ultra-low energy asynchronous processor for wireless sensor networks, " IEEE Int. Symposium on Asynchronous Circuits and Systems 2006, pp. 1-8.
- H. Lampinen, P. Perala, O. Vainio, "Design of a scalable asynchronous dataflow processor, " IEEE Design and Diagnostics of Electronic Circuits and systems (DATE) 2006, pp. 85-86.
- C. Jeong and S. M. Nowick, "Technology mapping and cell merger for asynchronous threshold networks, " IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 27, no. 4, pp. 659—672, 2008.
- A. J. Martin, P. Prakash, "Asynchronous nano-electronics: Preliminary investigation, " IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2008, pp. 58-68.
- J. Carmona, J. Cortadella, M. Kishinevsky, A. Taubin, "Elastic circuits, " IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 28, no. 10, pp. 1437—1455, 2009.
- A. Peeters, F. te Beest, M. de Wit, W. Mallon, "Click elements: An implementation style for data-driven compilation, " IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2010, pp. 3-14.
- S. Chaudhuri, W. Zhao, J.-O. Klein, C. Chappert, P. Mazoyer, "High density asynchronous LUT based on non-volatile MRAM technology, " IEEE Int. Conference on Field Programmable Logic and Applications (FPL) 2010, pp. 374—379.
- R. Ginosar, "Metastability and synchronizers: A tutorial, " IEEE Design & Test of Computers, vol. 28, no. 5, pp. 23-35, 2011.
- M. Y. Agyekum, S. M. Nowick, "Error-correcting unordered codes and hardware support for robust asynchronous global communication, " IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 31, no. 1, pp. 75-88, 2012.
- F.-C. Cheng, C. Chen, «Can QDI combinational circuits be implemented without C-elements?» IEEE Int. Symposium on Asynchronous Circuits and Systems (ASYNC) 2013, pp. 134—141.
- А. В. Сурков, "Использование Synopsys Design Compiler для синтеза самосинхронных схем, " Программные продукты и системы, vol. 4, no. 108, pp. 24-30, 2014.
- D. Lloyd and R. Illman, "Scan insertion and ATPG for C-gate based asynchronous designs, " Synopsys User Group (SNUG), 2014.
- J. Cortadella, M. Galceran-Oms, M. Kishinevsky and S. S. Sapatnekar, "RTL synthesis: From logic synthesis to automatic pipelining, " Proceedings of the IEEE, vol. 103, no. 11, pp. 2061—2075, 2015.
- J. Beaumont, "A survey of theory and practice in compositional design of asynchronous circuits, " Memo-2015-011, Newcastle University, 2015.
- Z. Tabassam, S. R. Naqvi, T. Akram, M. Alhussein, K. Aurangzeb and S. A. Haider, "Towards designing asynchronous microprocessors: From specification to tape-out, " IEEE Access, no. 5, vol. 7, pp. 33978-4003, 2019.
- A. de Gennaro, D. Sokolov, A. Mokhov, "Design and implementation of reconfigurable asynchronous pipelines, " IEEE Transactions on VLSI Systems, Vol. 28, no, 6, pp. 1527-39, 2020.
Патенты
- D. E. Muller, "Asynchronous encoder, " Patent US3017626, Jan. 16, 1962.
- S. R. Webb, "N pulse counter using at most 3n NOR elements for odd n and 3n/2 elements for even n, " Patent US3110821, Nov. 12, 1963.
- Б. Г. Сергеев, "Параллельный двоичный счетчик, " Авторское свидетельство SU217702, 07.05.1968.
- M. J. de Blauw, "Non-synchronous design for digital device control, " Patent US3460098, Aug. 5, 1969.
- С. С. Забара, Э. И. Комухаев, Г. И. Корниенко, "Кольцевой счетчик импульсов, " Авторское свидетельство SU249101, 18.08.1969.
- A. K. Rapp, "Bistable circuits, " Patent US3493785, Feb. 3, 1970.
- В. П. Морин и Е. Е. Попов, "Асинхронный регистр сдвига, " Авторское свидетельство SU374663, 20.03.1973.
- В. А. Грехнев и Б. Л. Останков, "Распределитель импульсов, " Авторское свидетельство SU416868, 25.02.1974.
- J. W. Foltz, "Binary universal flip-flop employing complementary insulated gate field effect transistors, " Patent US3835337, Sep. 10, 1974.
- А. Н. Фойда и Г. К. Шуляка, "Однотактный распределитель импульсов на кольцевом сдвигающем счетчике, " Авторское свидетельство SU451201, 25.11.1974.
- В. И. Варшавский, В. Б. Мараховский, И. А. Насибуллин и др., "Резервированный триггер, " Авторское свидетельство SU470914, 15.05.1975.
- T. Nanya, "Asynchronous spatial shift register circuit, " Patent US3893086, July 1, 1975.
- В. И. Горячев и Б. М. Мансуров, "Многостабильная пересчетная схема, " Авторское свидетельство SU507945, 25.03.1976.
- B. J. Clark and C. L Seitz, "Asynchronous self timed queue, " Patent US4058773, Nov. 15, 1977.
- Е. С. Павлов, "Трехстабильный счетный триггер, " Авторское свидетельство SU585591, 25.12.1977.
- S. S. Patil, "Asynchronous logic array, " Patent US4068214, Jan. 10, 1978.
- В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский и др., "Устройство для контроля переходных процессов в логических блоках, " Авторское свидетельство SU658561, 25.04.1979.
- C. Faustini, "Asynchronous circuit and system, " Patent US4167789, Sep. 11, 1979.
- В. И. Варшавский, В. Б. Мараховский, В. А. Песчанский и др., "Однотактный регистр сдвига, " Авторское свидетельство SU723683, 25.03.1980.
- В. А. Баранов, В. С. Баркан, Н. И. Бекасова и В. М. Степанцев, "Делитель частоты следования импульсов на три, " Авторское свидетельство SU849495, 23.07.1981.
- В. И. Горячев, "Многостабильный триггер, " Авторское свидетельство SU851786, 30.07.1981.
- Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU997261, 15.02.1983.
- Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1018245 , 15.05.1983.
- В. И. Варшавский и Б. С. Цирлин, "Двухфазный шестистабильный триггер, " Авторское свидетельство SU1072099, 07.02.1984.
- В. И. Варшавский, М. А. Кишиневский, Ю. В. Мамруков, В. Б. Мараховский и др., "Асинхронный регистр сдвига, " Авторское свидетельство SU1076951, 28.02.1984.
- Б. С. Цирлин, "Комбинационный сумматор, " Авторское свидетельство SU1078426, 07.03.1984.
- Б. С. Цирлин, "Асинхронный регистр сдвига, " Авторское свидетельство SU1117712, 07.10.1984.
- Б. С. Цирлин, "Асинхронный регистр сдвига, " Авторское свидетельство SU1119082, 15.10.1984.
- В. И. Варшавский, М. А. Кишиневский, Ю. В. Мамруков, В. Б. Мараховский и др., "Асинхронный регистр сдвига, " Авторское свидетельство SU1136216, 23.01.1985.
- С. С. Булгаков, В. И. Варшавский, В. И. Лазуткин, В. Б. Мараховский и др., "Асинхронный регистр сдвига, " Авторское свидетельство SU1138834, 07.02.1985.
- В. Ф. Мочалов, В. Н. Николаев и Е. К. Семенов, "Счетчик с последовательным переносом, " Авторское свидетельство SU1210220, 07.02.1986.
- Г. С. Брайловский, "Апериодический индикатор, " Авторское свидетельство SU1221719, 30.03.1986.
- В. И. Варшавский, О. В. Маевский, В. Б. Мараховский и др., "Триггерное устройство, " Авторское свидетельство SU1228221, 30.04.1986.
- Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1249714, 07.08.1986.
- В. А. Тетерин, Л. Ф. Викентьев, И. О. Синегубов и А. И. Дерябин, "IK-триггер, " Авторское свидетельство SU1256154, 07.09.1986.
- И. М. Лазер и Г. С. Брайловский, "Счетчик с последовательным переносом, " Авторское свидетельство SU1269257, 07.11.1986.
- Б. С. Цирлин и Г. С. Брайловский, "Апериодическое импульсное устройство (его варианты), " Авторское свидетельство SU1269239, 07.11.1986.
- В. И. Варшавский, В. Б. Мараховский, Л. Я. Розенблюм и Б. С. Цирлин, "Устройство для умножения, " Авторское свидетельство SU1335983, 07.09.1987.
- F. C. Furtek, "Programmable, asynchronous logic cell and array, " Patent US4700187, Oct. 13, 1987.
- В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский и др., "Комбинированный счетчик, " Авторское свидетельство SU1383490, 23.03.1988.
- Л. Я. Розенблюм, О. А. Федорова, А. В. Яковлев и И. В. Яценко, "Устройство для синхронизации модулей вычислительной системы, " Авторское свидетельство SU1442985, 07.12.1988.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Асинхронный последовательный регистр, " Авторское свидетельство SU1410103, 15.07.1988.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Асинхронный регистр сдвига на МДП-транзисторах, " Авторское свидетельство SU1411829, 23.07.1988.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1458968, 15.02.1989.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1465997, 15.03.1989.
- Л. Ф. Викентьев, И. О. Синегубов, О. Л. Лепихина и Т. Д. Коган, "Апериодический RS-триггер, " Авторское свидетельство SU1480098, 15.05.1989.
- В. И. Варшавский, В. Б. Мараховский, Л. Я. Розенблюм и В. И. Тимохин, "Триггерное устройство, " Авторское свидетельство SU1483614, 30.05.1989.
- В. И. Варшавский, В. Б. Мараховский, Н. М. Кравченко и Ю. С. Татаринов, "Счетчик в коде Грея, " Авторское свидетельство SU1492474, 07.07.1989.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Асинхронный последовательный регистр на КМДП-транзисторах, " Авторское свидетельство SU1494041, 15.07.1989.
- В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский и Б. С. Цирлин, "I-К-триггер, " Авторское свидетельство SU1504793, 30.08.1989.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и Б. С. Цирлин, "Пересчетная схема, " Авторское свидетельство SU1525909, 30.11.1989.
- В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский и В. М. Яккер, "Счетчик, " Авторское свидетельство SU1529448, 15.12.1989.
- В. И. Варшавский, Н. М. Кравченко, В. Б. Мараховский и Б. С. Цирлин, "Параллельный асинхронный регистр, " Авторское свидетельство SU1531172, 23.12.1989.
- A. Beltramini, "Differentiating logical circuit for asynchronous systems, " Patent US4943744, Jul. 24, 1990.
- С. Г. Арутюнян, "Асинхронный распределитель, " Авторское свидетельство SU1598141, 07.10.1990.
- В. И. Варшавский, В. И. Красюк, Н. М. Кравченко и В. Б. Мараховский, "Двоичный последовательный сумматор, " Авторское свидетельство SU1603377, 30.10.1990.
- В. И. Варшавский, В. И. Красюк, Н. М. Кравченко и В. Б. Мараховский, "Последовательный одноразрядный сумматор, " Авторское свидетельство SU1615703, 23.12.1990.
- В. И. Горячев, "Триггер IK-типа, " Авторское свидетельство SU1621143, 15.01.1991.
- В. И. Варшавский, А. Ю. Кондратьев и В. А. Романовский и Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1622935, 23.01.1991.
- В. И. Варшавский, А. Ю. Кондратьев, Н. М. Кравченко и В. Б. Мараховский, "Устройство для сравнения двух n-разрядных двоичных чисел, " Авторское свидетельство SU1640684, 07.04.1991.
- Н. А. Голдин, А. Ю. Кондратьев, В. А. Романовский и Б. С. Цирлин, "Парафазный одноразрядный комбинационный сумматор, " Авторское свидетельство SU1665372, 23.07.1991.
- Б. С. Цирлин, В. И. Варшавский, А. Ю. Кондратьев и В. А. Романовский, "Параллельный асинхронный регистр на КМДП-транзисторах, " Авторское свидетельство SU1665405, 23.07.1991.
- В. И. Варшавский, А. Ю. Кондратьев, В. А. Романовский и Б. С. Цирлин, "Асинхронный распределитель, " Авторское свидетельство SU1677858, 15.09.1991.
- L. Hluchý, B. Cirlin, B. Gaži, T. Pažurová and K. Košuk, "Zapojenie na prevod paralelného formátu znaku na sériovú postupnosť bitov, " Patent CS275655, 18.03.1992.
- L. Hluchý, B. Cirlin, B. Gaži, T. Pažurová and K. Košuk, "Zapojenie na prevod sériovej postupnosti na paralelný formát znaku, " Patent CS275656, 18.03.1992.
- T. E. Williams, "Zero overhead self-timed iterative logic, " Patent US5121003, Jun. 9, 1992.
- В. И. Варшавский, В. И. Красюк, Н. М. Кравченко и В. Б. Мараховский, "Реверсивный регистр сдвига, " Авторское свидетельство SU1817135, 23.05.1993.
- I. E. Sutherland, "Symmetric selector circuit for event logic, " Patent US5742182, Apr. 21, 1998.
- M. H. Sawasaki, C. Ykman-Couvreur, B. Lin, H. De Man, "System and method for generating a hazard-free asynchronous circuit, " Patent US5748487, May 5, 1998
- T. Nanya, "Asynchronous digital system, asynchronous data path circuit, asynchronous digital signal processing circuit and asynchronous digital signal processing method, Patent US6038259, Mar. 14, 2000
- Ю. А. Степченков, Ю. Г. Дьяченко, Ю. В. Рождественский и А. В. Рождественскене, "Разряд самосинхронного регистра сдвига, " Патент RU2319232, 10.03.2008.
- C. Jeong and S. M. Nowick, "Methods, media, and means for forming asynchronous logic networks, " Patent US7729893, Jun. 1, 2010.
- C. P. Sotiriou, A. Kondratyev, J. Cortadella and L. Lavagno, "Asynchronous, multi-rail, asymmetric-phase, static digital logic with completion detection and method for designing the same, " Patent US7870516, Jan. 11, 2011.
- В. Б. Мараховский, А. В. Сурков и С. Г. Бобков, "Модуль синхростратума для волновой обработки данных, " Патент RU2592462, 20.07.2016.
- В. Б. Мараховский, А. В. Сурков и С. Г. Бобков, "Модуль синхростратума, координирующий параллельную работу управляемого блока в глобально асинхронной системе, " Патент RU2592466, 20.07.2016.
- V. Khomenko, D. Sokolov, A. Yakovlev, "Tools and methods for selection of relative timing constraints in asynchronous circuits, and asynchronous circuits made thereby, " Patent US10839126, Nov. 17, 2020.



















![{\displaystyle [a',b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4612343e6070c6ec28bd9142e5aafef0700667)