Атака компромисса между временем/памятью/данными
Атака компромисса между временем/памятью/данными — тип криптографической атаки, при которой злоумышленник пытается достичь ситуации, аналогичной компромиссу времени и памяти, но с ещё одним параметром: объём данных, доступных злоумышленнику в режиме реального времени. Атакующий балансирует или уменьшает один или два из этих параметров в пользу другого или двух. Этот тип атаки очень сложен, и большинство шифров и схем шифрования не были разработаны, чтобы противостоять такому типу атак.
Эта атака представляет собой особый тип общей криптоаналитической атаки компромисса времени и памяти.
История
«Компромиссные» атаки на симметричные криптосистемы начались в 1980 году, когда Хеллман предложил метод компромисса времени и памяти[1].
В 1980 году Хеллман представил метод компромиссной атаки времени и памяти (TMTO) на блочные шифры. В более общем виде её можно рассматривать как одностороннюю функцию-инвертор. Оригинальная работа Хеллмана рассматривалась как инвертирующая односторонняя функция f в одной точке[1].
Бэббидж и Голич показали, что в контексте потоковых шифров несколько точек могут быть использованы другой компромиссной атакой, опираясь на парадокс дня рождения. Однако компромиссные атаки, основанные на парадоксе дня рождения также имеют проблемы: им не хватает гибкости из-за сильной связи сложности памяти со сложностью данных, что обычно приводит к нереалистичным данным или требованиям к памяти[2][3].
Позднее Бирюков и Шамир показали, что некоторые данные могут быть объединены с компромиссом Хеллмана, что приводит к гибкой формуле компромисса времени / памяти / данных[4].
Механика атаки
Эта атака является особым типом общей криптоаналитической атаки компромисса времени / памяти. Общая атака компромисса между временем и памятью состоит из двух основных фаз:
- Предварительная обработка: На этом этапе злоумышленник исследует структуру криптосистемы и может записывать свои результаты в большие таблицы. Это может занять много времени.
- Реальное время: На этом этапе криптоаналитику предоставляются реальные данные, полученные из определённого неизвестного ключа. Он или она пытается использовать предварительно вычисленную таблицу из фазы предварительной обработки, чтобы найти конкретный в как можно меньше времени.
Любая атака компромисса времени/памяти/данных имеет следующие параметры[5]:
- — размер пространства поиска
- — время, необходимое для фазы предварительной обработки
- — время, необходимое для фазы реального времени
- — объём памяти, доступной злоумышленнику
- — объём данных в реальном времени, доступных злоумышленнику
Хеллмановская компромиссная атака на блочные шифры
Для блочных шифров — это общее количество возможных ключей. Также, предполагается, что число возможных открытых текстов и шифротекстов равно . Также предположим что данные это единственный зашифрованный блок определённого аналога открытого текста.
Если рассмотреть маппинг ключа на зашифрованный текст как функцию случайной перестановки над точечным пространством , и если эта функция обратима; необходимо найти обратное этой функции . Метод Хеллмана, чтобы инвертировать эту функцию заключается в следующем[1]:
- На этапе предварительной обработки: Покроем пространство точек прямоугольной матрицей , которая создаётся путём итерации функции в случайных начальных точках в пространстве , и происходит это раз. Начальные точки — самый левый столбец в матрице, а конечные точки — самый правый столбец. Затем сохраняются пары начальной и конечной точек в порядке возрастания значений конечных точек.
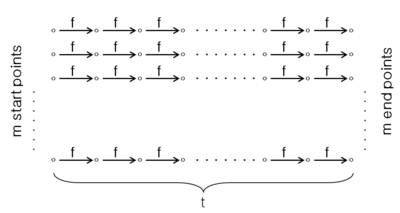
Hellman's Matrix
- Теперь только одна матрица не сможет покрыть все пространство . Но если добавить больше строк в матрицу, мы получим огромную матрицу, которая будет содержать восстановленные точки более одного раза.
- Таким образом, находится критическое значение , при котором матрица содержит ровно разных точек.
- Рассмотрим первые путей от начальных точек до конечных точек, которые не пересекаются с точками , так что следующий путь, который имеет хотя бы одну общую точку с одним из этих предыдущих путей и включает в себя ровно точек.
- Эти два набора точек и не пересекаются (исходя из парадокса дня рождения), если мы убедимся, что . Мы достигаем этого, применяя правило остановки матрицы: .
- Тем не менее, матрица с покрывает часть всего пространства.
- Чтобы сгенерировать для покрытия всего пространства, мы используем определённый вариант : и , что выполняется простыми манипуляциями, такими как переупорядочение битов [1]. И исходя из этого, общее время предварительной обработки составляет .
- Также , так как нам нужно хранить только пары начальных и конечных точек, и у нас есть матрицы , каждая из пар .
- В режиме реального времени Общее вычисление, необходимое для нахождения , равно , потому что нам нужно сделать попыток инверсии, так как оно может быть покрыто на одну матрицу, и каждая попытка занимает оценки некоторого . Оптимальная кривая компромисса получается с помощью правила остановки матрицы , и мы получаем , и выбор и зависит от стоимости каждого ресурса.
Согласно Хеллману, если блочный шифр обладает таким свойством, что маппинг его ключа на зашифрованный текст является функцией случайной перестановки над точечным пространством , и если эта является обратимой, компромиссные соотношения становятся намного лучше: [1].
Атаки Бэббиджа и Голича на потоковые шифры
Для потоковых шифров определяется числом внутренних состояний генератора битов — вероятно, отличается от количества ключей.
— это число первых псевдослучайных битов, генерируемых генератором.
Наконец, цель злоумышленника состоит в том, чтобы найти одно из фактических внутренних состояний генератора битов, чтобы иметь возможность запустить генератор с этого момента для генерации остальной части ключа. Связывается каждое из возможных внутренних состояний генератора битов с соответствующей строкой, состоящей из первых битов , полученных при запуске генератора из этого состояния с помощью отображения из состояний к префиксам [2].
Это отображение считается случайной функцией в общем пространстве точек . Чтобы инвертировать эту функцию, злоумышленник выполняет следующее[2]:
- На этапе предварительной обработки выбираются случайных состояний и вычисляются их соответствующие выходные префиксы
- Сохраняются пары в порядке возрастания в большой таблице.
- На этапе реального времени есть сгенерированных битов. Рассчитываются из них все возможных комбинаций последовательных битов с длиной .
- Находится каждый в сгенерированной таблице, который занимает время журнала.
- Если есть попадание, этот соответствует внутреннему состоянию генератора битов, из которого можно перезапустить генератор, чтобы получить остаток ключа.
- Парадоксом дня рождения гарантируется, что два подмножества пространства с точками имеют пересечение, если произведение их размеров больше, чем .
Этот результат атаки «дней рождения» даёт условие со временем атаки и временем предварительной обработки , которое является просто определённой точкой на кривой компромисса [2].
Можно обобщить это соотношение, если проигнорировать некоторые из доступных данных в режиме реального времени и получится уменьшить с до , и общая кривая компромисса в конечном итоге станет с и [2].
Атака компромисса между временем/памятью/данными, разработанная Шамиром и Бирюковым на потоковые шифры
Эта новая идея[4], представленная в 2000 году, сочетает в себе оба метода: компромисс Хеллмана[1] и атаки компромисса Бэббиджа и Голича[2][3], чтобы получить новую кривую компромисса с улучшенными границами для криптоанализа потоковых шифров[4].
Можно применить технику блочного шифра Хеллмана к потоковому шифру, используя ту же идею покрытия пространства точек через матрицы, полученные из нескольких вариантов функции , которая является отображением внутренних состояний на выходные префиксы[4].
Эта компромиссная атака на потоковый шифр успешна, если какой-либо из заданных выходных префиксов найден в любой из матриц, покрывающих . Следовательно, можно сократить количество покрываемых точек матрицами от точек до . Это достигается путём уменьшения количества матриц с до при сохранении максимально возможного размера (но для этого требуется, чтобы имел по крайней мере одну таблицу)[4].
Для этой новой атаки , так как уменьшилось количество матриц до и то же самое — для времени предварительной обработки . В реальном времени для атаки требуется , что представляет собой произведение количества матриц, длины каждой итерации и количества доступных точек данных во время атаки[4].
В конце концов, снова используется правило остановки матрицы для получения кривой компромисса для (потому что )[4].
Компромиссные атаки на потоковые шифры с низким сопротивлением выборки
Эту атаку изобрели Бирюков, Шамир, Вагнер[6].
Идея опирается на следующую особенность различных потоковых шифров: генератор битов претерпевает лишь несколько изменений во внутреннем состоянии перед созданием следующего выходного бита. Следовательно, можно перечислить те состояния, которые генерируют нулевых битов для небольших значений при низких затратах[6].
Но, когда большое количество выходных битов принимает конкретные значения, этот процесс перечисления становится очень дорогим и сложным. Теперь можно определить сопротивление выборки потокового шифра как с максимальным значением , которое делает возможным такое перечисление[6].
Пусть потоковый шифр имеет состояния , каждое из которых имеет полное имя битов и соответствующее имя выхода, которые являются первыми битами в выходной последовательности битов. Если этот потоковый шифр имеет сопротивление выборки , то эффективное перечисление может использовать короткое имя из битов для определения определённых состояний генератора[6].
Каждое состояние с коротким именем имеет соответствующее короткое имя вывода из битов, которое является выходной последовательностью состояния после удаления первых начальных битов . Теперь возможно определить новое отображение по уменьшенному пространству точек , и это отображение эквивалентно исходному отображению[6].
Если , данные в реальном времени, доступные злоумышленнику, гарантированно получится по крайней мере один выход из этих состояний. В противном случае, необходимо ослабить определение состояний, чтобы включить больше точек[6].
Если заменить на и на в новой атаке на обмен времени / памяти / данных Шамира и Бирюкова, получится такая же кривая компромисса , но с [6].
Это на самом деле улучшение, так как возможно было бы ослабить нижнюю границу , поскольку может быть небольшим до , что означает, что атака может быть выполнена быстрее[6].
Ещё одно преимущество этого метода заключается в том, что сократилось количество дорогостоящих операций доступа к диску с до , поскольку будет запрашиваться доступ только к специальным точкам . И это также может значительно ускорить атаку из-за уменьшения количества дорогостоящих дисковых операций[6].
Пример атаки на схему паролей в Unix-системах
Атаки, описанные в этой статье, не ограничиваются блочными или потоковыми шифрами, они применимы к другим односторонним конструкциям, например, к хеш-функциям[7].
Компромисс времени / памяти / данных можно использовать для анализа паролей Unix, например, если злоумышленник получает доступ к хранилищу файлов хешей паролей крупной организации (D = 1000 хэшей паролей)[7].
В самом деле, пространство компромисса состоит из 56 битов неизвестного ключа (то есть пароля) и 12 бит известной соли. Поскольку размер соли намного короче размера ключа, его эффект от усложнения компромисса не очень значителен[7].
Предположим, что злоумышленник знает, что пароли выбираются из набора произвольных 8-символьных буквенно-цифровых паролей, включая заглавные буквы и два дополнительных символа как точка и запятая, которые в сумме могут быть закодированы в 48 бит. Таким образом, вместе с 12-битной солью состояние N = 260 бит[7].
Например, параметры следующей атаки кажутся довольно практичными: время предварительной обработки выполняется один раз: P = N / D = 250 Unix хеш-вычисления, распараллеливаемые. Память M = 234 8-байтовых записей (12 + 48 бит), занимает один жёсткий диск размером 128 ГБ. Таким образом, мы храним 234 стартовых указателей. Тогда время атаки равно T = 232 оценкам Unix-хеша — примерно час на быстром ПК или около 8 секунд на BEE2 FPGA[8].
Атака будет восстанавливать один пароль из каждых 1000 новых хэшей паролей. Относительно длительный этап предварительной обработки может выполняться параллельно в сети ПК (на сотню ПК может уйти меньше месяца) или около 1,5 месяцев для одной BEE2 FPGA. Количество таблиц рассчитывается параллельно и может достигать t / D = 217/1000 = 27[8].
Чтобы уменьшить количество запросов к жёсткому диску, атака должна будет использовать отличительные точки с 16-битным префиксами. Это позволит сделать только 216 обращений к диску (что меньше 6 минут)[8].
На самом деле ясно, что такой компромисс может проанализировать все пароли, набираемые на клавиатуре. Пространство N = 848 · 212 = 263. Предполагая снова D = 210, мы получаем время предварительного вычисления P = 253, M = 235 8-байтовых записей или один жёсткий диск размером 256 ГБ, Т = 236 оценок хешей[8].
Примечания
- ↑ 1 2 3 4 5 6 Hellman, M.E., "A cryptanalytic time-memory trade-off, " Information Theory, IEEE Transactions on, vol.26, no.4, pp.401,406, Jul 1980
- ↑ 1 2 3 4 5 6 Babbage, S. H., "Improved «exhaustive search» attacks on stream ciphers, " Security and Detection, 1995., European Convention on, vol., no., pp.161-166, 16-18 May 1995
- ↑ 1 2 Golic, J., «Cryptanalysis of Alleged A5 Stream Cipher» Архивная копия от 25 августа 2017 на Wayback Machine Lecture Notes in Computer Science, Advances in Cryptology — EUROCRYPT ’97, LNCS 1233, pp.239-255, Springer-Verlag 1997
- ↑ 1 2 3 4 5 6 7 Biryukov A., Shamir A., «Cryptanalytic Time/Memory/Data Tradeoffs for Stream Ciphers» Lecture Notes in Computer Science, Advances in Cryptology — ASIACRYPT 2000, LNCS 1976, pp.1-13, Springer-Verlag Berlin Heidelberg 2000
- ↑ Архивированная копия. Дата обращения: 19 ноября 2020. Архивировано 17 октября 2020 года.
- ↑ 1 2 3 4 5 6 7 8 9 Biryukov A., Shamir A., Wagner D., «Real Time Cryptanalysis of A5/1 on a PC» Архивная копия от 25 июля 2018 на Wayback Machine Fast Software Encryption 2000, pp.1-18, Springer-Verlag 2000
- ↑ 1 2 3 4 Khoongming Khoo, Guanhan Chew, Guang Gong, Hian-Kiat Lee. Time-Memory-Data Trade-off Attack on Stream Ciphers based on Maiorana-McFarland Functions. — 2007. — № 242. Архивировано 16 декабря 2018 года.
- ↑ 1 2 3 4 Nele Mentens, Lejla Batina, Bart Preneel, Ingrid Verbauwhede. Time-Memory Trade-Off Attack on FPGA Platforms: UNIX Password Cracking. — 2006-08-03. — С. 323–334. — doi:10.1007/11802839_41. Архивировано 17 декабря 2018 года.





























































