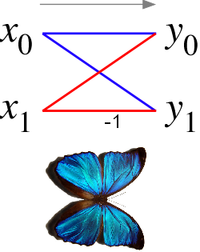Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
В численном и функциональном анализе дискретные вейвлет-преобразования (ДВП) относятся к вейвлет-преобразованиям, в которых вейвлеты представлены дискретными сигналами (выборками).
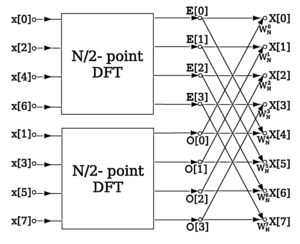
Быстрое преобразование Фурье — алгоритм ускоренного вычисления дискретного преобразования Фурье, позволяющий получить результат за время, меньшее чем 
. Иногда под быстрым преобразованием Фурье понимается один из алгоритмов, называемый алгоритмом прореживания по частоте — времени, имеющий сложность 
.
Автокорреляционная функция (АКФ) — зависимость взаимосвязи между функцией (сигналом) и её сдвинутой по аргументу функции копией от величины сдвига.
Шаблон:Карточка стандарта
Метод умножения Шёнхаге — Штрассена — алгоритм умножения больших целых чисел, основанный на быстром преобразовании Фурье, требует 
) битовых операций, где 
— количество двоичных цифр в произведении.
SHARK — симметричный алгоритм блочного шифрования, разработанный группой криптографов, среди которых Винсент Рэймен, — автор шифра AES. В теории позволяет использовать блоки и ключи различной длины, однако авторская реализация использует 128-битный ключ и 64-битные блоки. Структура схожа со структурой подстановочно-перестановочной сети.
Модифицированное дискретное косинус-преобразование (МДКП) является преобразованием Фурье и основывается на дискретном косинусном преобразовании (ДКП-IV). Это преобразование с перекрытием. Оно выполняется на последовательных блоках объемных наборов данных, каждый из последующих блоков перекрывается. Это происходит следующим образом: вторая половина предыдущего блока совпадает с первой половиной следующего. Такое перекрытие, вдобавок к функциям ДКП, делает МДКП особенно полезным для сжатия сигналов тех приложений, где необходимо избежать появления артефактов, которые обычно выходят за границы блоков.
Длинная арифметика — выполняемые с помощью вычислительной машины арифметические операции над числами, разрядность которых превышает длину машинного слова данной вычислительной машины. Эти операции реализуются не аппаратно, а программно, с использованием базовых аппаратных средств работы с числами меньших порядков. Частный случай — арифметика произвольной точности — относится к арифметике, в которой длина чисел ограничена только объёмом доступной памяти.
Алгоритм Гёрцеля — это специальная реализация дискретного преобразования Фурье (ДПФ) в форме рекурсивного фильтра. Данный алгоритм был предложен Джеральдом Гёрцелем в 1958 году. В отличие от быстрого преобразования Фурье, вычисляющего все частотные компоненты ДПФ, алгоритм Гёрцеля позволяет эффективно вычислить значение одного частотного компонента.
Алгоритм Фюрера — быстрый метод умножения больших целых чисел. Алгоритм был построен в 2007 году швейцарским математиком Мартином Фюрером из университета штата Пенсильвания как асимптотически более быстрый алгоритм, чем его предшественник, алгоритм Шёнхаге — Штрассена, опубликованный в 1971 году. Задача быстрого умножения больших чисел представляет большой интерес в области криптографии с открытым ключом.
Преобразование Вигнера — Вилла — один из эффективных методов спектрально-временного анализа нестационарных сигналов. Встречаются другие названия: преобразование Вигнера — Вилля, распределение Вигнера — Вилла, распределение Вигнера — Вилля, функция Вигнера.
SWIFFT — набор криптографических хеш-функций с доказанной стойкостью. Они основываются на быстром преобразовании Фурье и используют алгоритм LLL-редуцированных базисов. Криптографическая стойкость функций SWIFFT математически доказана при использовании рекомендуемых параметров. Поиск коллизий в SWIFFT в худшем случае требует не меньше временных затрат, чем нахождение коротких векторов в циклических/идеальных решётках. Практическое применение SWIFFT будет ценно именно в тех случаях, когда стойкость к коллизиям особенно важна. Например, цифровые подписи, которые должны оставаться надёжными длительное время.
Задача о триангуляции многоугольника — классическая задача комбинаторной и вычислительной геометрии, состоящая в нахождении триангуляции многоугольника без дополнительных вершин.
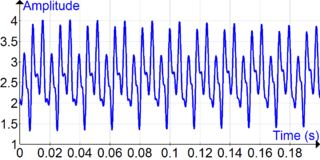
Анализ Фурье — направление в анализе, изучающее каким образом общие математические функции могут быть представлены либо приближены через сумму более простых тригонометрических функций. Анализ Фурье возник при изучении свойств рядов Фурье, и назван в честь Жозефа Фурье, который показал, что представление функции в виде суммы тригонометрических функций значительно упрощает изучение процесса теплообмена.
Алгоритм Бернштейна — Вазирани — квантовый алгоритм, решающий задачу нахождения 
-битного числа, скрытого в черном ящике. Предложен Итаном Бернштейном и Умешем Вазирани в 1993 году. Данный алгоритм решает поставленную задачу значительно быстрее, чем это возможно в неквантовой постановке. Алгоритм может применяться в базах данных, атаках на блочные шифры, тестах производительности для квантовых компьютеров, был реализован на 5- и 16-кубитных квантовых компьютерах IBM.
Быстрое преобразование Хафа — модификация преобразования Хафа, позволяющая параметрически идентифицировать прямые с меньшей вычислительной сложностью за счет использования факта самопересечения рассматриваемых дискретных прямых.
Вычисление значений многочлена — определение точных значений многочлена в заданном наборе точек. Одним из традиционных методов вычисления значений многочлена является метод Горнера. Помимо этого, существуют параллельные алгоритмы для решения данной задачи, а также быстрые методы для вычисления значений многочлена в нескольких точках одновременно. Существуют также специальные алгоритмы для решения частных случаев данной задачи, такие как алгоритм Блуштайна и быстрое преобразование Фурье.
