Бент-функция

Бент-функция (от англ. bent — «изогнутый, наклонённый»[1], [2]) — булева функция с чётным числом переменных, для которой расстояние Хэмминга от множества аффинных булевых функций с тем же числом переменных максимально. Бент-функции в этом смысле обладают максимальной степенью нелинейности среди всех функций с данным числом переменных и благодаря этому широко применяются в криптографии для создания шифров, максимально устойчивых к методам линейного и дифференциального криптоанализа[1].
В русскоязычной литературе используется близкий по смыслу термин «максимально нелинейная функция», число переменных таких функций не ограничивается чётными числами. Максимально нелинейная функция с чётным числом переменных является бент-функцией [1].
Определения
Расстояние Хэмминга для двух булевых функций n переменных — количество различий в значениях этих функций на полном множестве из 2n наборов переменных.
Аффинная (линейная) булева функция — булева функция, полином Жегалкина которой не имеет нелинейных членов, то есть членов, представляющих собой конъюнкцию нескольких переменных.
Степень нелинейности булевой функции deg(f) — число переменных в самом длинном слагаемом её полинома Жегалкина.
Нелинейность булевой функции N(f) — расстояние Хэмминга от данной функции до множества всех аффинных функций.
История
Бент-функции были введены в 1960-х годах Оскаром Ротхаузом (1927—2003), который в это время (с 1960 по 1966 годы) работал Институте оборонного анализа (IDA), где занимался криптографическими исследованиями. Его первая работа по бент-функциям относится к 1966 году[3], однако она была засекречена и в открытой печати появилась только в 1976 году[4].
В 1960-х годах В.А.Елисеев и О.П.Степченков занимались исследованием бент-функций в СССР, однако их работы до сих пор засекречены[1]. Известно, что они называли бент-функции "минимальными функциями" и предложили конструкцию МакФарланда еще в 1962 году.
Свойства
Нелинейность бент-функций с числом переменных n (n — чётное) определяется соотношением [1], [2]:
- .
Для максимально нелинейных функций с нечётным числом переменных точное выражение для нелинейности неизвестно[1].
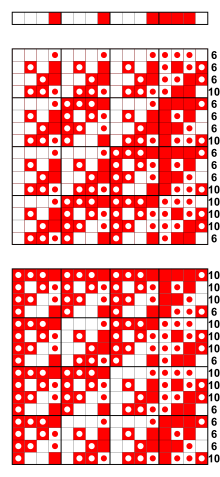
Примеры бент-функций
Ниже приведены примеры бент-функций четырёх, шести и восьми переменных[5].
Монография
В книге [1] приведен детальный обзор результатов в области бент-функций. Рассматривается история открытия бент-функций, описываются их приложения в криптографии и дискретной математике. Исследуются основные свойства и эквивалентные представления бент-функций, классификации бент-функций от малого числа переменных, комбинаторные и алгебраические конструкции бент-функций, связь бент-функций с другими криптографическими свойствами. Изучаются расстояния между бент-функциями и группа автоморфизмов бент-функций. Рассматриваются верхние и нижние оценки числа бент-функций и гипотезы о его асимптотическом значении. Приводится детальный систематический обзор 25 различных обобщений бент-функций, рассматриваются открытые вопросы в данной области. Книга [1] 2015 года содержит более 125 теорем о бент-функциях и существенно расширяет книгу [2] , опубликованную в 2011 году.
Примечания
- ↑ 1 2 3 4 5 6 7 8 N. Tokareva. Bent functions: results and applications to cryptography (англ.) // Acad. Press. Elsevier, 2015. 220 pages. : journal. Архивировано 30 ноября 2016 года.
- ↑ 1 2 3 Токарева Н. Н. Нелинейные булевы функции: бент-функции и их обобщения Архивная копия от 14 июля 2012 на Wayback Machine // Издательство LAP LAMBERT Academic Publishing (Saarbrucken, Germany), 2011. ISBN 978-3-8433-0904-2. 180 с.
- ↑ Rothaus O. On bent functions // IDA CRD W.P. No. 169. 1966.
- ↑ O. S. Rothaus. On "Bent" Functions (англ.) // Journal of Combinatorial Theory, Series A : journal. — 1976. — May (vol. 20, no. 3). — P. 300—305. — ISSN 0097-3165. — doi:10.1016/0097-3165(76)90024-8. Архивировано 20 сентября 2022 года.
- ↑ Молдовян А.А. Криптография. Скоростные шифры // БХВ-Петербург, 2002. ISBN 594157214X, ISBN 9785941572144. 496 c.