Бикупол
| Множество бикуполов | ||
|---|---|---|
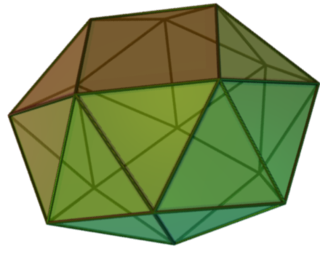
 Пример: кубооктаэдр | ||
| Тип | Многогранник Джонсона | |
| Свойства | выпуклый | |
| Комбинаторика | ||
| Элементы |
| |
| Грани | 2n треугольников, 2n квадратов 2 n-угольников | |
| Классификация | ||
| Группа симметрии | Орто: Dnh, [2,n], *n22, порядок 4n Гиро: Dnd, [2+,2n], 2*n, порядок 4n | |

Бикупол — тело, образованное соединением двух куполов по основанию.
Существует два класса бикуполов, поскольку каждый купол (половина многогранника) по периметру имеет перемежающиеся треугольники и квадраты. Если соприкасаются одинаковые типы граней, результатом будет ортокупол (или прямой бикупол), если же квадраты смежны треугольникам, результатом будет гирокупол (или повёрнутый бикупол).
Куполы и бикуполы существуют как бесконечные множества многогранников, точно так же, как множества пирамид, бипирамид, призм и трапецоэдров.
Шесть бикуполов имеют в качестве граней правильные многоугольники — это треугольные, квадратные и пятиугольные орто- и гирокупола. Треугольный гирокупол является архимедовым телом (кубооктаэдром). Остальные пять являются многогранниками Джонсона.
Бикуполы более высоких порядков можно построить, если допускается растяжение боковых граней в прямоугольники и равнобедренные треугольники.
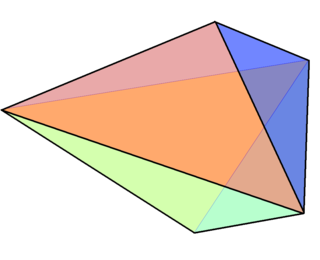
Бикуполы являются специфичными многогранниками, имеющими по четыре грани, смежные любой вершине. Это означает, что их двойственные многогранники будут иметь все грани четырёхугольными. Наиболее известным примером служит ромбододекаэдр, состоящий из 12 ромбических граней. Двойственным многогранником ортоформы, треугольный ортобикупол[англ.], является додекаэдр, похожий на ромбододекаэдр, но он имеет 6 трапециевидных граней, которые перемежаются и образуют кольцо.
Виды
Множество ортобикуполов
| Симметрия | Рисунок | Описание |
|---|---|---|
| D2h [2,2] *222 |  | Дигональный ортобикупол или бифастигиум: 4 треугольников (копланарные пары), 4 квадратов |
| D3h [2,3] *223 |  | Треугольный ортобикупол[англ.] (J27): 8 треугольников, 6 квадратов. Двойственным является трапецеромбический додекаэдр |
| D4h [2,4] *224 |  | Квадратный ортобикупол[англ.] (J28): 8 треугольников, 10 квадратов |
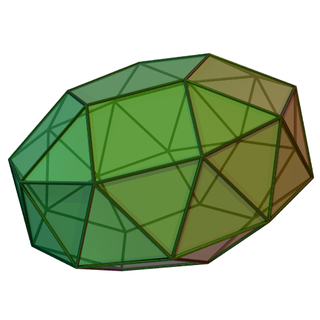
| D5h [2,5] *225 |  | Пятиугольный ортобикупол[англ.] (J30): 10 треугольников, 10 квадратов, 2 пятиугольников |
| Dnh [2,n] *22n | n-угольный ортобикупол: 2n треугольников, 2n квадратов, 2 n-угольников |
Множество гиробикуполов
| Симметрия | Рисунок | Описание |
|---|---|---|
| D2d [2+,4] 2*2 |  | Гиробифастигиум (J26): 4 треугольников, 4 квадратов |
| D3d [2+,6] 2*3 |  | Треугольный гиробикупол или октаэдр: 8 треугольников, 6 квадратов. Его двойственным является ромбододекаэдр |
| D4d [2+,8] 2*4 |  | Квадратный гиробикупол[англ.] (J29): 8 треугольников, 10 квадратов |
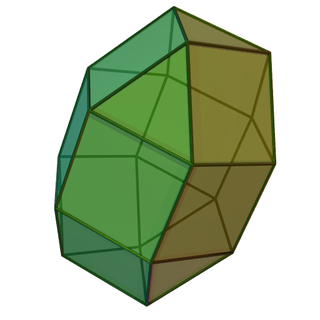
| D5d [2+,10] 2*5 | Пятиугольный гиробикупол[англ.] (J31): 10 треугольников, 10 квадратов, 2 пятиугольника | |
| Dnd [2+,2n] 2*n | n-угольный гиробикупол: 2n треугольников, 2n квадратов, 2 n-угольников |
Примечания
- Norman W. Johnson. Convex Solids with Regular Faces. — Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169–200. Содержит перечисление 92 тел и гипотезу, что других нет.
- Victor A. Zalgaller. Convex Polyhedra with Regular Faces. — Consultants Bureau, 1969. Первое доказательство, что существует только 92 тел Джонсона.
- В. А. Залгаллер. Выпуклые многогранники с правильными гранями // Зап. научн. сем. ЛОМИ. — 1967. — Т. 2. Доказательство, что существует только 92 тел Джонсона.