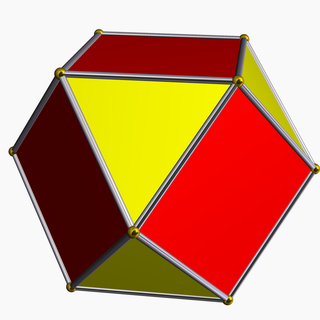
Большой великий звёздчатый стодвадцатиячейник
| Большой великий звёздчатый стодвадцатиячейник | |
|---|---|
 Ортогональная проекция | |
| Тип | Многогранник Шлефли–Гесса |
| Ячейки | 120 {5/2,3} |
| Грани | 720 {5/2} |
| Рёбра | 1200 |
| Вершины | 600 |
| Вершинная фигура | {3,3} |
| Символ Шлефли | {5/2,3,3} |
| Диаграммы Коксетера — Дынкина | |
| Группа симметрии | H4, [3,3,5] |
| Двойственный | Великий шестистоячейник[англ.] |
| Свойства | Правильный |

Большой великий звёздчатый стодвадцатиячейник или большой великий звёздчатый полидодекаэдр — правильный звёздчатый 4-мерный многогранник с символом Шлефли {5/2,3,3}, один из 10 правильных 4-мерных многогранников Шлефли–Гесса. Этот многогранник имеет 600 вершин и то же самое расположение вершин[англ.], что и выпуклый правильный стодвадцатиячейник.
Многогранник является одним из четырёх правильных звёздчатых четырёхмерных многогранников, открытых Людвигом Шлефли. Название многограннику дал Джон Хортон Конвей как расширение системы имён Артура Кэли для тел Кеплера — Пуансо, и это единственный многогранник, содержащий три модификатора в имени.
Рисунки
| H4 | A2 / B3 | A3 / B2 |
|---|---|---|
| Большой великий звёздчатый стодвадцатиячейник, {5/2,3,3} | ||
 |  |  |
| [10] | [6] | [4] |
| стодвадцатиячейник, {5,3,3} | ||
 |  |  |
Как звёздчатая форма
Большой великий звёздчатый стодвадцатиячейник является конечной стадией приведения к звёздчатой форме стодвадцатиячейника и это единственный многогранник Шлефли–Гесса, имеющий стодвадцатиячейник в качестве выпуклой оболочки. В этом смысле многогранник аналогичен трёхмерному большому звёздчатому додекаэдру, который является конечной стадией приведения к звёздчатой форме додекаэдра и единственным многогранником Кеплера — Пуансо, имеющим додекаэдр в качестве выпуклой оболочки. Более того, большой великий звёздчатый стодвадцатиячейник двойственен великому шестисотячейнику[англ.], который можно рассматривать как четырёхмерный аналог большого икосаэдра, который двойственен большому звёздчатому додекаэдру.
См. также
- Список правильных многогранников и соединений
- Правильные выпуклые 4-мерные многогранники
- Многогранники Кеплера — Пуансо - правильные звёздчатые многогранники
Примечания
- ↑ В английском — zome = zonohedron + dome (зоноэдр + здание)
Литература
- Edmund Hess. Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder. — 1883.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. (Chapter 26) // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- H.S.M. Coxeter. Regular Polytopes[англ.]. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — С. 124. — ISBN 0-486-61480-8.
- Richard Klitzing, 4D uniform polytopes (polychora), o3o3o5/2x – gogishi