Большой триамбикикосаэдр

Большой триамбикикосаэдр и средний триамбикикосаэдр в геометрии являются внешне идентичными двойственными однородными^[англ.] многогранниками, относятся к группе сферической симметрии I_h.

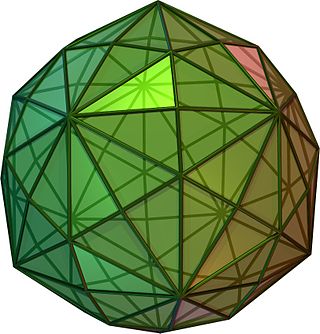
Внешняя поверхность представляет собой звездообразную форму икосаэдра. Эти фигуры можно отличить, определив, какие пересечения между ребрами являются истинными вершинами, а какие нет.

На приведенных изображениях истинные вершины отмечены золотыми сферами, которые можно увидеть в вогнутых Y-образных областях. В качестве альтернативы, если грани заполнены по правилу четный-нечетный, внутренняя структура обеих фигур будет отличаться.

12 вершин выпуклой оболочки соответствуют расположению вершин^[англ.] икосаэдра.

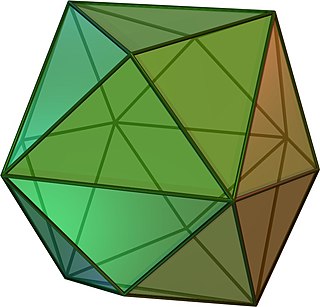
Большой триамбикикосаэдр — двойственный (дуальный) многогранник к большому битригональному икосододекаэдру^[англ.]

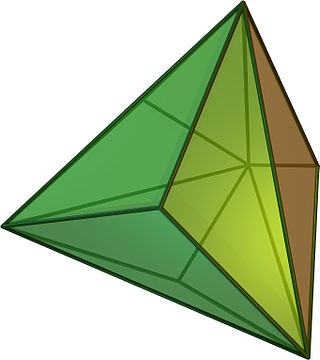
Большой триамбикикосаэдр имеет 20 шестиугольных граней, по форме напоминающих трехлопастной винт (пропеллер). У него 32 вершины: 20 внешних точек и 20 скрытых внутри. Он имеет 60 ребер.

У граней чередующиеся углы, равные ${\displaystyle \arccos \left({\frac {1}{4}}\right)-60^{\circ }\approx 15.52248781407}$ и ${\displaystyle \arccos \left(-{\frac {1}{4}}\right)\approx 104.47751218593^{\circ }}$. Сумма шести углов равна ${\displaystyle 360^{\circ }}$, а не ${\displaystyle 720^{\circ }}$, как у шестиугольника, поскольку многоугольник дважды поворачивается вокруг своего центра. Двугранный угол равен ${\displaystyle \arccos \left(-{\frac {1}{3}}\right)\approx 109.47122063449}$.

Средний триамбикикосаэдр — двойственный (дуальный) многогранник к битригональному додекаэдру^[англ.].

Средний триамбикикосаэдр имеет 20 граней, каждая из которых представляет собой простые вогнутые изотоксальные шестиугольники или треугольники. У него 24 вершины: 12 внешних точек и 12 скрытых внутри. Он имеет 60 ребер.

В отличие от большого триамбикикосаэдра, средний триамбикикосаэдр топологически является правильным многогранником с индексом 2^[1].

Это 34-я модель Веннинджера, 9-я звездчатая форма икосаэдра.

• Триакисикосаэдр
• Малый триамбический икосаэдр
• Средний ромбический триаконтаэдр^[англ.]

• М. Веннинджер. Модели многогранников. — «Мир», 1974.
• Wenninger, Magnus (1983). Dual Models. Cambridge University Press.
• H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, 3.6 6.2 Stellating the Platonic solids, pp. 96–104
• The Regular Polyhedra (of index two), David A. Richter

• Weisstein, Eric W. «Great triambic icosahedron». MathWorld.
• Weisstein, Eric W. «Medial triambic icosahedron». MathWorld.
• gratrix.net Uniform polyhedra and duals
• bulatov.org Medial triambic icosahedron Great triambic icosahedron