Вектор состояния может означать:
Ква́нтовая (волнова́я) меха́ника — фундаментальная физическая теория, которая описывает природу в масштабе атомов и субатомных частиц. Она лежит в основании всей квантовой физики, включая квантовую химию, квантовую теорию поля, квантовую технологию и квантовую информатику.
Спин — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с движением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.
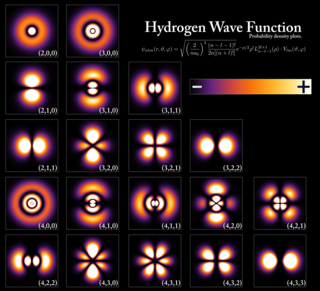
Волнова́я фу́нкция, или пси-фу́нкция 
Квантовое состояние — любое возможное состояние, в котором может находиться квантовая система. Чистое квантовое состояние может быть описано:
Кот Шрёдингера — мысленный эксперимент, предложенный одним из создателей квантовой механики Эрвином Шрёдингером в 1935 году при обсуждении физического смысла волновой функции. В ходе эксперимента возникает суперпозиция живого и мёртвого кота, что выглядит абсурдно с точки зрения здравого смысла.
Фазовое пространство в математике и физике — пространство, на котором представлено множество всех состояний системы так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Матрица плотности — один из способов описания состояния квантовомеханической системы. В отличие от волновой функции, пригодной лишь для описания чистых состояний, оператор плотности в равной мере может задавать как чистые, так и смешанные состояния. Основанный на понятии оператора плотности формализм был предложен независимо Л. Д. Ландау и Дж. фон Нейманом в 1927 году и Ф. Блохом в 1946 году.
Измерение в квантовой механике — концепция, описывающая возможность получения информации о состоянии системы путём проведения физического эксперимента.
Эта статья включает описание термина «полная энергия»
Нулевы́е колеба́ния — флуктуации квантовой системы в основном состоянии, наинизшем по энергии, обязанные своим существованием принципу неопределённости.
При́нцип соотве́тствия в методологии науки — утверждение, что любая новая научная теория должна включать старую теорию и ее результаты как частный случай. Например, закон Бойля — Мариотта является частным случаем уравнения состояния идеального газа в приближении постоянной температуры; кислоты и основания Аррениуса являются частным случаем кислот и оснований Льюиса и т. п.
Коммутатором операторов 
T-симме́три́я — симметрия уравнений, описывающих законы физики, по отношению к операции замены времени t на −t. В квантовой механике математически записывается, как равенство нулю коммутатора оператора Гамильтона и антиунитарного оператора обращения времени
Унитарный оператор — ограниченный линейный оператор 
,Оператор — линейное отображение в одной из областей физики — квантовой механике, которое действует на волновую функцию, являющуюся комплекснозначной функцией, дающей наиболее полное описание состояния системы. Операторы обозначаются большими латинскими буквами с циркумфлексом наверху:
Математические основы квантовой механики — принятый в квантовой механике способ математического моделирования квантовомеханических явлений, позволяющий вычислять численные значения наблюдаемых в квантовой механике величин. Были созданы Луи де-Бройлем, В. Гейзенбергом, Э. Шрёдингером, Н. Бором. Завершил создание математических основ квантовой механики и придал им современную форму П. А. М. Дирак. Отличительным признаком математических уравнений квантовой механики является наличие в них символа постоянной Планка.
Бра и кет — алгебраический формализм, предназначенный для описания квантовых состояний. Называется также обозначениями Дирака. В матричной механике данная система обозначений является общепринятой. Данная система обозначений представляет собой не более чем иные текстуальные обозначения для векторов, ковекторов, билинейных форм и скалярных произведений, и потому применима в линейной алгебре вообще. В тех случаях, когда данная система обозначений используется в линейной алгебре, обычно речь идет о бесконечно-мерных пространствах и/или о линейной алгебре над комплексными числами.
По́лная систе́ма коммути́рующих наблюда́емых (ПСКН) — множество перестановочных (коммутирующих) самосопряжённых операторов, описывающих квантовые наблюдаемые и определяющих обобщённый базис пространства чистых состояний квантовой системы. Это понятие впервые было предложено Дираком и является одним из основных в квантовой механике. Обобщенные собственные значения операторов ПСКН называются квантовыми числами.
Матричная квантовая механика — это формулировка квантовой механики, созданная Вернером Гейзенбергом, Максом Борном и Паскуалем Йорданом в 1925 году. Матричная квантовая механика была первой концептуально автономной и логически непротиворечивой формулировкой квантовой механики. Её описание квантовых скачков заменило модель Бора для электронных орбит. Это было сделано путём интерпретации физических свойств частиц как матриц, которые эволюционируют во времени. Матричная механика эквивалентна волновой формулировке Шрёдингера квантовой механики на основе теоремы Риса — Фишера, как это проявляется в обозначениях бра и кет Дирака.
Симметрии в квантовой механике — преобразования пространства-времени и частиц, которые оставляют неизменными уравнения квантовой механики. Рассматриваются во многих разделах квантовой механики, которые включают релятивистскую квантовую механику, квантовую теорию поля, стандартную модель и физику конденсированного состояния. В целом, симметрия в физике, законы инвариантности и сохранения являются основополагающими ограничениями для формулирования физических теорий и моделей. На практике это мощные методы решения задач и прогнозирования того, что может случиться. Хотя законы сохранения не всегда дают конечное решение проблемы, но они формируют правильные ограничения и наметки к решению множества задач.