Непрерывная функция — функция, которая меняется без мгновенных «скачков», то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
Интегра́л Ри́мана — наиболее широко используемый вид определённого интеграла. Очень часто под термином «определённый интеграл» понимается именно интеграл Римана, и он изучается самым первым из всех определённых интегралов во всех курсах математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.

Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций.
Признак Дирихле — теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна Дирихле.
Теоре́ма Лебе́га о мажори́руемой сходи́мости в функциональном анализе, теории вероятностей и смежных дисциплинах — это теорема, утверждающая, что если сходящаяся почти всюду последовательность измеримых функций может быть ограничена по модулю сверху интегрируемой функцией, то все члены последовательности, а также предельная функция тоже интегрируемы. Более того, интеграл последовательности сходится к интегралу её предела.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).
Первая теорема о среднем значении — одна из теорем об определённом интеграле.
Интегральное исчисление — раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений.

Интегра́л — одно из важнейших понятий математического анализа, которое возникает при решении задач:
- о нахождении площади под кривой;
- пройденного пути при неравномерном движении;
- массы неоднородного тела, и тому подобных;
- а также в задаче о восстановлении функции по её производной.
Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида. Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции. В терминах функционального анализа, определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Примечание: всюду в данной статье, где используется знак  имеется в виду (кратный) интеграл Римана
имеется в виду (кратный) интеграл Римана  , если не оговорено обратное;
, если не оговорено обратное;
всюду в данной статье, где говорится об измеримости множества, имеется в виду измеримость по Жордану, если не оговорено обратное.

Формула Ньютона — Лейбница, или основная формула анализа, или формула Барроу даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Кратный интеграл — определённый интеграл, взятый от  переменных; например:
переменных; например:
 .
.
Криволинейный интеграл — интеграл, вычисляемый вдоль какой-либо кривой.
Если функция интегрируема по Риману на отрезке, то она ограничена на этом отрезке.
Как и для криволинейных интегралов, существуют два рода поверхностных интегралов.
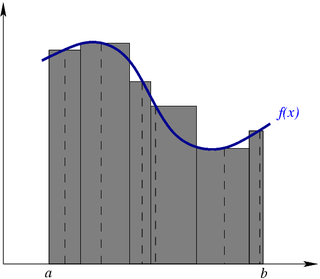
Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0..
Смешанные частные производные одной и той же функции, отличающиеся лишь порядком (очерёдностью) дифференцирования, равны между собой при условии их непрерывности. Такое свойство называется равенством смешанных производных.
Теорема Вейля о равномерном распределении формулирует критерий равномерной распределённости бесконечной последовательности вещественных чисел из отрезка  .
.


![{\displaystyle \xi \in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cc05d1fb45b90e25c99bc6a57473d508d3e9c23)


















