Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.

Торсио́н — стержень из упругого материала, имеющий относительно небольшую крутильную жёсткость, высокую упругость и работающий на кручение.
Тензор Риччи, названный в честь итальянского математика Грегорио Риччи-Курбастро, задаёт один из способов измерения кривизны многообразия, то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства. Тензор Риччи, точно так же как метрический тензор, является симметричной билинейной формой на касательном пространстве риманова многообразия. Грубо говоря, тензор Риччи измеряет деформацию объёма, то есть степень отличия n-мерных областей n-мерного многообразия от аналогичных областей евклидова пространства (см. геометрический смысл тензора Риччи). Обычно обозначается  или
или  .
.

Поверхностные состояния, — электронные состояния, пространственно локализованные вблизи поверхности твёрдого тела.

Сопло́ Лава́ля — газовый канал особого профиля для изменения скорости проходящего по нему газового потока. Широко используется на некоторых типах паровых турбин и является важной частью современных ракетных двигателей и сверхзвуковых реактивных авиационных двигателей.
Изгиб — в сопротивлении материалов вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев, изменение кривизны/искривление срединной поверхности пластины или оболочки. Изгиб связан с возникновением в поперечных сечениях бруса или оболочки изгибающих моментов. Прямой изгиб балки возникает в случае, когда изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, изгиб называется косым.
Длина свободного пробега молекулы — это среднее расстояние  , которое пролетает частица за время между двумя последовательными столкновениями.
, которое пролетает частица за время между двумя последовательными столкновениями.
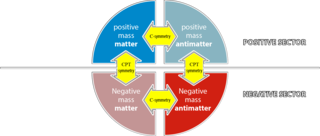
Биметрические теория гравитации — альтернативные теории гравитации, в которых вместо одного метрического тензора используются два или более. Часто вторая метрика вводится только при высоких энергиях, в предположении, что скорость света может зависеть от энергии. Наиболее известными примерами биметрических теорий являются теория Розена и релятивистская теория гравитации.
В математике линейное дифференциальное уравнение имеет вид

Уравнение Фридмана — в космологии уравнение, описывающее развитие во времени однородной и изотропной Вселенной в рамках общей теории относительности. Названо по имени Александра Александровича Фридмана, который первым вывел это уравнение в 1922 году.
Уравне́ние Кортеве́га — де Фри́за — нелинейное уравнение в частных производных третьего порядка, играющее важную роль в теории нелинейных волн, в основном гидродинамического происхождения. Впервые было получено Жозефом Буссинеском в 1877 году, но подробный анализ был проведён уже Дидериком Кортевегом и Густавом де Врисом в 1895 году.

Модифицированный потенциал Пёшль — Теллера — функция потенциальной энергии элетростатического поля, предложенная физиками Гертой Пёшль и Эдвардом Теллером как приближение для энергии двухатомной молекулы, альтернативный потенциалу Морзе


Гауссова кривизна — мера искривления поверхности в окрестности какой-либо её точки. Гауссова кривизна является объектом внутренней геометрии поверхностей, то есть она не изменяется при изометрических изгибаниях.

Крути́льные весы́ — физический прибор, предназначенный для измерения малых сил или моментов сил.
Физические свойства графена проистекают из электронных свойств атомов углерода и поэтому часто имеют нечто общее с остальными аллотропными модификациями углерода, которые были известны до него, такими как графит, алмаз, углеродные нанотрубки. Конечно, схожести больше с графитом, так как он состоит из графеновых слоёв, но без новых уникальных физических явлений и исследований других материалов и наработок физических методов анализа и теоретических подходов графен не привлёк бы специалистов из таких разных дисциплин как физика, химия, биология и физика элементарных частиц.
Зависимость масса — светимость — в астрофизике уравнение, показывающее связь между массой звезды и её светимостью. Данное уравнение имеет вид

Бимомент — физическая величина, изгибно-крутящий момент, образуется при нагрузке профиля, расположенного под углом или при неравномерной нагрузке на профиль.
Теория изгиба балок Тимошенко была развита Степаном Прокофьевичем Тимошенко в начале XX века. Модель учитывает сдвиговую деформацию и вращательные изгибы, что делает её применимой для описания поведения толстых балок, сэндвич-панелей и высокочастотных колебаний балок, когда длина волны этих колебаний становится сравнимой с толщиной балки. В отличие от модели изгиба балок Эйлера-Бернулли модель Тимошенко приводит к уравнению четвертого порядка, которое также содержит и частные производные второго порядка. Физически учёт механизмов деформации эффективно снижает жёсткость балки и приводит к большему отклонению при статической нагрузке и к предсказанию меньших собственных частот для заданного набора граничных условий. Последнее следствие наиболее заметно для высоких частот, поскольку длина волны колебаний становится короче и расстояние между противоположно направленными сдвиговыми силами уменьшается.

Тео́рия пласти́н — раздел теории упругости, в котором рассматриваются упругие тела с толщиной много меньше, чем остальные геометрические размеры. Сведение трёхмерной задачи теории упругости к двумерной и её решение являются основными темами теории пластин. Общий вопрос теории заключается в нахождении уравнений, отвечающих за связи между деформациями и напряжениями при различных допущениях. В случае тонких пластин и малых прогибов применяют теорию Кирхгофа — Лява. Большие прогибы тонких пластин описываются уравнениями Фёппля — фон Кармана. Для упругих свойств толстых пластин применяют теорию Миндлина. Исторически теория пластин развивалась в связи с многочисленными практическими применениями в строительстве, а позже — в кораблестроении и самолётостроении, где важны расчёты на прочность.





















