Гармонограф

Гармоно́граф — механический прибор, использующий маятники для создания геометрического изображения. Создаваемые рисунки обычно представляют собой кривые Лиссажу или связанные с ними рисунки большей сложности. Изобретение этих устройств, которые начали появляться в середине 19 века и достигли пика популярности в 1890-х годах, не может быть окончательно приписано одному человеку, хотя официальным изобретателем принято считать Хью Блэкберна, профессора математики из Университета Глазго[1].
Простой, так называемый "боковой" гармонограф использует два маятника для управления движением пера относительно поверхности чертежа. Один маятник перемещает перо вперед-назад вдоль одной оси, а другой маятник перемещает поверхность чертежа вперед-назад вдоль перпендикулярной оси. Изменяя частоту и фазу движения маятников относительно друг друга, можно создавать различные фигуры. Даже простой гармонограф, описанный выше, может чертить эллипсы, спирали, восьмерки и другие фигуры Лиссажу.
Более сложные гармонографы с более сложным движением пера по бумаге включают в себя несколько отдельных или даже соединенных вместе маятников (например, один маятник может быть подвешен к другому).
Особый тип гармонографа — пинтограф[2] — основан на относительном движении двух вращающихся дисков.
История создания
В 1870-х годах термин "гармонограф" упоминается в связи с А. Е. Донкиным и устройствами, созданными Сэмюэлем Чарльзом Тисли[3].
Маятник Блэкбёрна
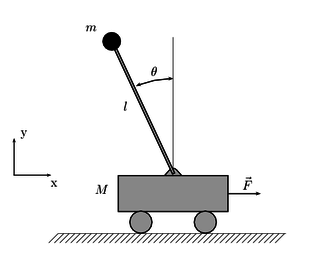
Маятник Блэкберна — это устройство для иллюстрации простого гармонического колебания. Он был назван в честь Хью Блэкберна, который описал его в 1844 году. Впервые он был рассмотрен Джеймсом Дином в 1815 году и математически проанализирован Натаниэлем Боудичем в том же 1844 году[4]. Маятник подвешивается к струне, которая в свою очередь подвешена к V-образной паре струн, так что маятник колеблется одновременно в двух перпендикулярных направлениях с разными периодами. В результате маятник движется по траектории, напоминающей кривую Лиссажу; он относится к семейству механических устройств, известных как гармонографы[5].
В учебниках по физике середины XX века этот тип маятника иногда называют двойным маятником.
Математическое описание действия
Гармонограф создает свои фигуры с помощью движения затухающих маятников. Движение затухающего маятника описывается уравнением:
- где — частота,
- — фаза,
- — амплитуда,
- — затухание
- — время.
Если маятник может двигаться вокруг двух осей (круговой или эллиптической формы), то в силу принципа суперпозиции движение стержня, соединенного с нижней частью маятника, вдоль одной оси будет описываться уравнением:
Типичный гармонограф имеет два маятника, которые движутся подобным образом, и ручку, которая перемещается двумя перпендикулярными стержнями, соединенными с этими маятниками. Поэтому траектория движения фигуры гармонографа описывается параметрическими уравнениями:
Соответствующая компьютерная программа может перевести эти уравнения в график, эмулирующий гармонограф. Применяя первое уравнение к каждому уравнению второй раз, можно эмулировать движущийся лист бумаги.
 Принцип работы механического гармонографа с одним маятником. В качестве пера здесь используется цветной фломастер.
Принцип работы механического гармонографа с одним маятником. В качестве пера здесь используется цветной фломастер.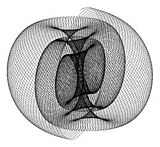 Изображение, созданное гармонографом с двумя маятниками.
Изображение, созданное гармонографом с двумя маятниками. Изображение, созданное пинтографом.
Изображение, созданное пинтографом.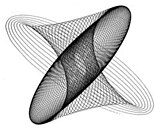 Изображение, созданное гармонографом с двумя маятниками.
Изображение, созданное гармонографом с двумя маятниками.
Список примечаний
- ↑ Turner, Steven (February 1997). "Demonstrating Harmony: Some of the Many Devices Used To Produce Lissajous Curves Before the Oscilloscope". Rittenhouse. 11 (42): 41.
- ↑ Пинтограф не следует путать с пантографом, который представляет собой механическое устройство, используемое для увеличения фигур.
- ↑ Robert J. Whitaker. Harmonographs. II. Circular design // American Journal of Physics. — 2001-02. — Т. 69, вып. 2. — С. 174–183. — ISSN 1943-2909 0002-9505, 1943-2909. — doi:10.1119/1.1309522.
- ↑ Leslie P. Pook. Understanding pendulums. — Dordrecht: Springer, 2013. — Т. 12. — 133 с. — (History of mechanism and machine science). — ISBN 978-94-007-3634-4.
- ↑ Baker, Gregory L.; Blackburn, James A. (2005). The Pendulum: a case study in physics. Oxford. ISBN 978-0-19-156530-4