Гептамино

Перейти к навигацииПерейти к поиску

Гептамино — семиклеточное полимино, то есть плоская фигура, состоящая из семи равных квадратов, соединённых сторонами. С фигурами гептамино, как со всеми полимино, связано много задач занимательной математики.

108 фигур гептамино

Если не считать различными фигуры, совпадающие при поворотах и зеркальных отражениях, то различных («двусторонних», «свободных») форм гептамино насчитывается 108 (см. рисунок)[1][2]. Существует 196 видов «односторонних» гептамино (если зеркальные отражения считаются различными фигурами) и 760 видов «фиксированных» гептамино (различными считаются также и повороты)[3].

Классификация гептамино по симметрии

108 свободных фигур гептамино по их свойствам симметрии можно разделить на 6 категорий:

  • 84 фигур гептамино (на рисунке изображены серым цветом) асимметричны;
  • 9 гептамино (изображены красным) имеют ось симметрии, параллельную линиям квадратной сетки;
  • 7 гептамино (изображены зелёным) имеют диагональную ось симметрии;
  • 4 гептамино (изображены синим) имеют центральную (вращательную) симметрию второго порядка;
  • 3 гептамино (изображены фиолетовым) имеют две оси симметрии, параллельных линиям сетки;
  • 1 гептамино (изображено оранжевым) имеет две диагональных оси симметрии.

Для односторонних гептамино (т.е. если зеркальные отражения фигур считать различными), первая и четвёртая категории удваиваются в численности, что даёт дополнительно 88 гептамино, т.е. в общей сложности 196. Для фиксированных гептамино (т.е. если повороты также рассматривать как различные фигуры), то первая категория возрастёт в восемь раз по сравнению со свободными гептамино, следующие три категории — в четыре раза, а две последние категории — в два. Это даст фиксированных гептамино.

Составление фигур из гептамино

Среди 108 свободных гептамино есть одна фигура с отверстием («неодносвязная»). Из этого следует, что сплошное покрытие какого-либо прямоугольника площадью квадратов полным набором гептамино невозможно. (Невозможно также покрыть полным набором гептамино прямоугольник площадью в 757 квадратов с отверстием в 1 квадрат, поскольку 757 — простое число, а составить из гептамино прямоугольник 1×757, очевидно, невозможно).

Три прямоугольника с отверстиями, составленные из 108 гептамино

Тем не менее, из полного набора в 108 гептамино можно сложить три прямоугольника 11×23, каждый с одноклеточным отверстием в центре[4]. Разумеется, вокруг одного из этих отверстий должно располагаться неодносвязное гептамино. Комбинируя эти прямоугольники разными способами, можно получить прямоугольник 33×23 или 11×69 с тремя симметрично расположенными отверстиями.

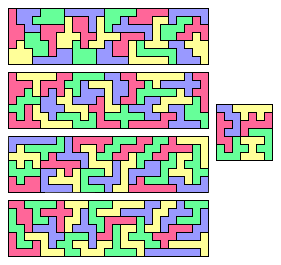
Четыре прямоугольника и квадрат, составленные из 107 односвязных гептамино

Если отбросить неодносвязное гептамино, из остальных 107 односвязных фигур (общей площадью 749 квадратов) можно различными способами составить прямоугольник 7×107. В частности, из них можно сложить четыре прямоугольника 7×25 и один квадрат 7×7[4].

Из всех 108 гептамино можно сложить 12 одинаковых шахматных досок 8 × 8, в каждой из которых удалено одно и то же поле[5][6]. Patrick Hamlyn осуществил эту конструкцию, используя окрашенные в три цвета гептамино (36 гептамино каждого из трёх цветов), так, что одноцветные фигуры не касаются друг друга. Затем, не меняя раскраски фигур, из всех гептамино каждого из трёх цветов можно сложить прямоугольник 11 × 23 с удалённым центральным мономино[5].

Псевдогептамино

Псевдополимино — обобщение полимино, набор полей бесконечной шахматной доски, которые может обойти король[1]. Существует 3031 двустороннее[7], 5931 одностороннее[8] и 23 592 фиксированных[9] псевдогептамино.

Примечания

  1. ↑ 1 2 Голомб, 1975.
  2. ↑ Golomb, 1994.
  3. ↑ Weisstein, Eric W. Heptomino (англ.) на сайте Wolfram MathWorld.
  4. ↑ 1 2 Задачи впервые решил Дэвид А. Клэрнер (Голомб, 1975, с. 119).
  5. ↑ 1 2 Ed Pegg Jr. G4G5 Talk. A very nice heptomino solution by Patrick Hamlyn. MathPuzzle.com. Дата обращения: 20 ноября 2015. Архивировано 5 сентября 2015 года.
  6. ↑ Ed Pegg Jr. Christopher Monckton's Eternity and other new polyforms. MathPuzzle.com. Дата обращения: 20 ноября 2015. Архивировано 4 марта 2016 года.
  7. ↑ Последовательность A030222 в OEIS
  8. ↑ Последовательность A030233 в OEIS
  9. ↑ Последовательность A006770 в OEIS

Литература

  • Голомб С.В.. Полимино = Polyominoes / Пер. с англ. В. Фирсова. Предисл. и ред. И. Яглома. — М.: Мир, 1975. — 207 с.
  • Solomon W. Golomb. Polyominoes. — 2nd ed. — Princeton, New Jersey: Princeton University Press, 1994. — ISBN 0-691-02444-8.
  • D. Hugh Redelmeier. Counting polyominoes: yet another attack // Discrete Mathematics : журнал. — 1981. — Vol. 36. — P. 191–203. — doi:10.1016/0012-365X(81)90237-5.
  • Daniel A. Rawsthorne. Tiling complexity of small n-ominoes (n<10) // Discrete Mathematics : журнал. — 1988. — Vol. 70. — P. 71–75. — doi:10.1016/0012-365X(88)90081-7.
  • Glenn C. Rhoads. Planar tilings by polyominoes, polyhexes, and polyiamonds // Journal of Computational and Applied Mathematics : журнал. — 2005. — Vol. 174. — P. 329–353. — doi:10.1016/j.cam.2004.05.002.