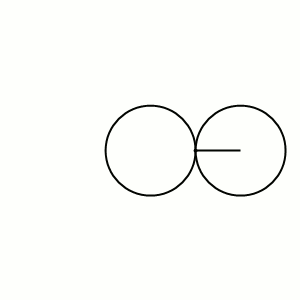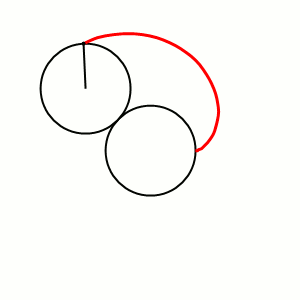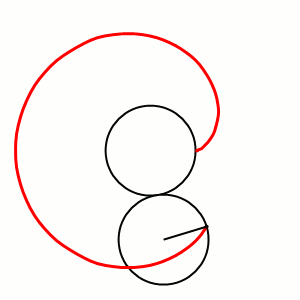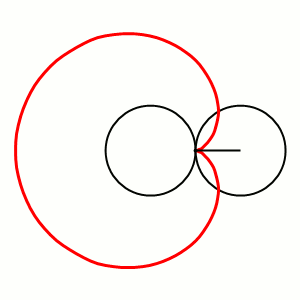Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Циссоида Диокла — плоская алгебраическая кривая третьего порядка. В декартовой системе координат, где ось абсцисс направлена по  , а ось ординат по
, а ось ординат по  , на отрезке
, на отрезке  , как на диаметре строится вспомогательная окружность. В точке
, как на диаметре строится вспомогательная окружность. В точке  проводится касательная
проводится касательная  . Из точки
. Из точки  проводится произвольная прямая
проводится произвольная прямая  , которая пересекает окружность в точке
, которая пересекает окружность в точке  и касательную в точке
и касательную в точке  . От точки
. От точки  , в направлении точки
, в направлении точки  , откладывается отрезок
, откладывается отрезок  , длина которого равна длине отрезка
, длина которого равна длине отрезка  . При вращении линии
. При вращении линии  вокруг точки
вокруг точки  , точка
, точка  описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.
описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.
Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
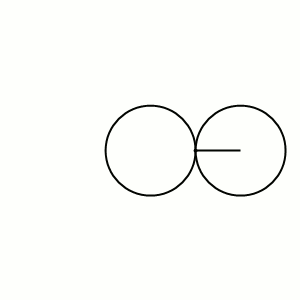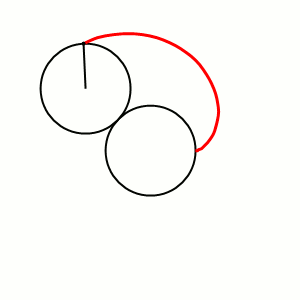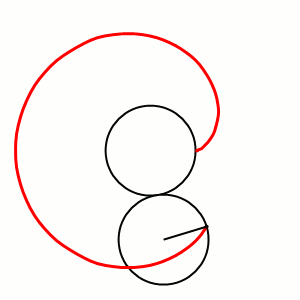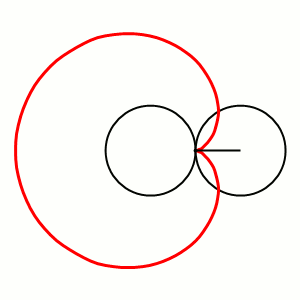
Кардио́ида, или сердцеви́дная крива́я — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

Жезл, литуус — плоская трансцендентная кривая, определяемая уравнением :
 ,
,
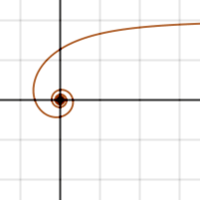
Логарифми́ческая спира́ль или изогональная спираль — особый вид спирали, часто встречающийся в природе.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое описывает
- электростатическое поле,
- гравитационное поле,
- стационарное поле температуры,
- поле давления,
- поле потенциала скорости в гидродинамике.
Антидеси́ттеровское простра́нство — псевдориманово многообразие постоянной отрицательной кривизны. Его можно считать псевдоримановым аналогом  -мерного гиперболического пространства. Названо как противопоставление пространству де Ситтера, обозначается обычно
-мерного гиперболического пространства. Названо как противопоставление пространству де Ситтера, обозначается обычно  .
.
Волновое уравнение в физике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты, которая задаёт высоту точки над плоскостью.
Задача Шту́рма — Лиуви́лля, названная в честь Жака Шарля Франсуа Штурма и Жозефа Лиувилля, состоит в отыскании нетривиальных решений на промежутке  уравнения Штурма — Лиувилля
уравнения Штурма — Лиувилля

Здесь приведён список векторных дифференциальных операторов в различных системах координат.

Лемниската Бута — плоская алгебраическая кривая четвёртого порядка, частный случай кривой Персея. Названа в честь Джеймса Бута.
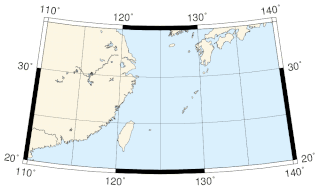
Проекция Альберса — картографическая проекция, разработанная в 1805 году немецким картографом Хейнрихом Альберсом (1773—1833). Используется для изображения регионов, вытянутых в широтном направлении. Проекция коническая, сохраняющая площадь объектов, но искажающая углы и форму контуров. Параллели в этой проекции отображаются в виде концентрических окружностей, а меридианы — в виде прямых, проходящих через одну точку. Переменными проекции являются две главные параллели, искажения на которых равны нулю.
Тороидальная система координат — ортогональная система координат в пространстве, координатными поверхностями которой являются торы, сферы и полуплоскости. Данная система координат может быть получена посредством вращения двумерной биполярной системы координат вокруг оси, равноудалённой от фокусов биполярной системы.

Равновеликая азимутальная проекция Ламберта — это способ проекции с поверхности сферы на поверхность круга. Эта проекция сохраняет площади, но не сохраняет углы. Проекция носит имя швейцарского математика Иоганна Генриха Ламберта, который представил её в 1772 году.
Ме́тод Га́усса в небесной механике и астродинамике используется для первоначального определения параметров орбиты небесного тела по трём наблюдениям.