Ри́манова геоме́трия — раздел дифференциальной геометрии, главным объектом изучения которого являются римановы многообразия, то есть гладкие многообразия с дополнительной структурой, римановой метрикой, иначе говоря — с выбором евклидовой метрики на каждом касательном пространстве, причём эта метрика гладко меняется от точки к точке. Иногда, особенно часто в математической физике, под римановой геометрией подразумевают также и псевдориманову геометрию многообразий с псевдоримановой метрикой, например, геометрию пространства-времени специальной и общей теории относительности.
Индикатриса Дюпена или индикатриса кривизны — плоская кривая, которая даёт наглядное представление об искривленности поверхности в данной её точке.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.
Линейчатая поверхность ― поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой.

Теорема Лиувилля о конформных отображениях утверждает, что

Геометрия Римана — одна из неевклидовых геометрий постоянной кривизны. Если геометрия Евклида реализуется в пространстве с нулевой гауссовой кривизной, Лобачевского — с отрицательной, то геометрия Римана реализуется в пространстве с постоянной положительной кривизной.

Параболо́ид ― тип поверхности второго порядка в трёхмерном евклидовом пространстве.
Точка округления ― точка на гладкой регулярной поверхности в евклидовом пространстве, в которой нормальные кривизны по всем направлениям равны.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.

Алексе́й Васи́льевич Погоре́лов — советский математик. Специалист в области выпуклой и дифференциальной геометрии, теории дифференциальных уравнений и теории оболочек. Академик АН СССР / РАН. Лауреат Ленинской премии.

Никола́й Влади́мирович Ефи́мов — советский математик, член-корреспондент АН СССР (1979). Лауреат Ленинской премии.
Отображение Гаусса — отображение из гладкой поверхности в трёхмерном евклидовом пространстве в единичную сферу, при котором точка поверхности отображается в вектор единичной нормали в этой точке. Названо в честь Карла Фридриха Гаусса.
Дифференциальная геометрия поверхностей — исторически важная область дифференциальной геометрии.

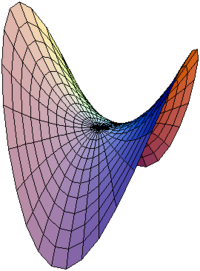
Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. Является точкой равновесия в чистых стратегиях. В такой точке, если рассматривается функция двух переменных, образованная графиком функции поверхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями.

Обезьяньим седлом называется поверхность, определяемая уравнением:


Седловая поверхность — гладкая поверхность, все точки которой седловые, то есть имеют отрицательную гауссову кривизну.

Развёртывающаяся поверхность, или торс, ― поверхность, обладающая нулевой гауссовой кривизной.
Седловая точка в математике может обозначать:
- Седловая точка функции — точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом.
- Седловая точка поверхности — точка, для которой поверхность лежит локально по разные стороны от своей касательной плоскости проведённой в этой точке.
- Седловая точка матрицы — элемент матрицы, связанный с равновесием Нэша в теории игр.
Алексей Леонидович Вернер — советский и российский учёный в области математики, доктор физико-математических наук (1969), профессор (1971), педагог, автор школьных учебников геометрии, заслуженный деятель науки Российской Федерации (1995), почётный профессор Российского государственного педагогического университета им. А. И. Герцена (2001), почётный доктор Новгородского Государственного Университета им. Ярослава Мудрого (2004).