Гипогамильтонов граф

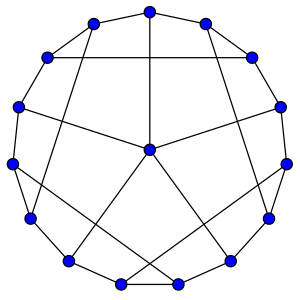
В теории графов говорят, что граф G гипогамильтонов, если сам по себе граф не имеет гамильтонова цикла, но любой граф, полученный удалением одной вершины из G, является гамильтоновым.

Гипогамильтоновы графы первым изучал Сусельер в 1963^[2]. Линдгрен^[1] цитирует Гаудина, Герца и Росси (1964)^[3], а также Бусакера и Саати (1965)^[4] в качестве дополнительного материала по данной тематике. Ещё одна ранняя работа — статья Герца, Дуби и Виге 1967 года^[5].

Грётчел^[6] просуммировал большинство работ в этой области следующим высказыванием: «Статьи об этих графах ... обычно выявляют новые классы гипогамильтоновых и гиповычерчиваемых графов и показывают, что для некоторых n такие графы действительно существуют или что они обладают странными и неожиданными свойствами.»

Гипогамильтоновы графы появляются в целочисленных решениях задачи коммивояжёра – гипогамильтоновы графы определённого вида определяют фасеты многогранника коммивояжёра, тела, определённого как выпуклая оболочка множества возможных решений задачи коммивояжёра, и эти фасеты можно использовать для методов отсекающих плоскостей при решении задачи алгоритмом Гомори^[7][6][8]. Грётчел заметил^[6], что вычислительная сложность определения, является ли граф гипогамильтоновым, хотя и не известна, по-видимому, высока, что делает трудным поиск фасет такого типа, за исключением фасет, определённых гипогамильтоновыми графами малых размеров. К счастью, наиболее маленькие графы приводят к наиболее сильным неравенствам для данной задачи^[9].

Понятия, близкие гипогамильтоновости, использовали Парк, Лим и Ким^[10] для измерения отказоустойчивости сетевых топологий параллельных вычислений.

Любой гипогамильтонов граф должен быть вершинно 3-связным, так как удаление любых двух вершин оставляет гамильтонов путь, который связен (в графе с удалённой одной вершиной существует гамильтонов цикл, а удаление второй вершины даёт гамильтонов путь) . Существуют гипогамильтоновы графы с n вершинами, в которых максимальная степень вершины равна n/2 и в которых примерно n²/4 рёбер^[11].

Герц, Дуби и Виге высказали гипотезу^[5], что любой гипогамильтонов граф имеет обхват 5 или более, но гипотеза была опровергнута Томассеном^[12], нашедшим примеры с обхватом 3 и 4. Некоторое время не было известно, могут ли гипогамильтоновы графы быть планарными, но теперь известны некоторые примеры таких графов ^[13] и наименьший из этих графов имеет 40 вершин ^[14]. Любой планарный гипогамильтонов граф имеет по меньшей мере одну вершину только с тремя инцидентными рёбрами^[15].

Если 3-однородный граф гамильтонов, его рёбра могут быть выкрашены в три цвета — используем поочерёдную раскраску рёбер двумя цветами вдоль гамильтонова цикла (который должен иметь чётную длину по лемме о рукопожатиях), а третьим цветом выкрашиваем все оставшиеся рёбра. Таким образом, все снарки, кубические графы без мостов, требующие четыре цвета для раскраски рёбер, должны быть негамильтоновы, и многие из известных снарков гипогамильтоновы. Любой гипокамильтонов снарк является бикритичным — удаление любых двух вершин оставляет подграф, рёбра которого можно выкрасить в три цвета^[16][17]. Трёхцветную раскраску этого подграфа можно легко описать — после удаления вершины оставшаяся часть содержит гамильтонов цикл. После удаления второй вершины цикл становится путём, рёбра которого можно поочерёдно выкрасить двумя цветами. Оставшиеся рёбра образуют паросочетание и все эти рёбра можно выкрасить третьим цветом.

Классы цветов любой 3-цветной раскраски рёбер 3-однородного графа образуют три паросочетания, таких, что каждое ребро принадлежит ровно одному паросочетанию. Гипогамильтоновы снарки не имеют разложения на паросочетания такого типа, но Хеггквист^[18] высказал гипотезу, что рёбра любого гипогамильтонова снарка могут быть использованы для образования шести паросочетаний, таких, что каждое ребро принадлежит ровно двум паросочетаниям. Это специальный случай гипотезы Бержа – Фулкерсона, что любой снарк имеет шесть паросочетаний с таким свойством.

Гипогамильтоновы графы не могут быть двудольными — в двудольном графе вершина может быть удaлена с образованием гамильтонова подграфа, только если она принадлежит к большему из двух классов цветов графа. Однако любой двудольный граф встречается в виде порождённого подграфа некоторого гипогамильтонова графа^[19].

Самый маленький гипогамильтонов граф — это граф Петерсена^[5]. Более общо, обобщённый граф Петерсена GP(n,2) является гипогамильтоновым, если n равен 5 (mod 6) ^[20]. Граф Петерсена является представителем этого построения с n = 5.

Линдгрен^[1] нашёл другой бесконечный класс гипогамильтоновых графов, в котором число вершин равно 4 (mod 6). Построение Линдгрена состоит из цикла длины 3 (mod 6) и одной центральной вершины. Центральная вершина соединена с каждой третьей вершиной цикла ребром, которое он называет спицей, а вершины на две позиции от конечной вершины спицы соединяются друг с другом. Снова наименьшим представителем построения Линдгрена является граф Петерсена.

Дополнительные бесконечные семейства дали Бонди^[21], Дойен и ван Дист^[22] и Гутт^[23].

Вацлав Хватал в 1973 доказал, что для всех достаточно больших n существует гипогамильтонов с n вершинами. Если принять во внимание последовавшие открытия^[24][22], «достаточно большое число» теперь известно, так что такие графы существуют для всех n ≥ 18. Полный список гипогамильтоновых графов с не более чем 17 вершинами известен ^[25] — это граф Петерсена с 10 вершинами, графы с 13 и 15 вершинами, найденные Герцем с помощью компьютерного поиска^[26], и четыре графа с 16 вершинами. Существует по меньшей мере тринадцать гипогамильтоновых графов с 18 вершинами. При применении триггерного метода Хватала^[27] к графу Петерсена и снарку «цветок», можно показать, что число гипогамильтоновых графов, конкретнее, число гипогамильтоновых снарков, растёт как экспонента от числа вершин^[28][29].

Теоретики изучают также гиповычерчиваемые графы, графы, не содержащие гамильтонов путь, но в которых любое подмножество n − 1 вершин может быть соединено путём^{[30][31][32][24]}. Аналогичные определения гипогамильтоновости и гиповычерчиваемости были предложены некоторыми авторами для ориентированных графов^{[33][34][35][15]}.

Эквивалентное определение гипогамильтоновых графов — что их самые длинные циклы имеют длину n − 1 и что пересечение всех самых длинных циклов пусто. Менке и Замфиреску^[36] исследовали графы со свойством, что пересечение самых длинных циклов пусто, но в которых длина таких циклов меньше n − 1. Герц^[26] определил циклируемость графа как наибольшее число k, такое, что любые k вершин принадлежат циклу. Гипогамильтоновы графы — это в точности графы, которые имеют циклируемость n − 1. Подобным образом Парк, Лим и Ким^[10] определил граф как ƒ-устойчиво негамильтонов, если удаление самое большее ƒ вершин даёт гамильтонов подграф. Шауэрте и Замфиреску^[37] изучали графы с циклируемостью n − 2.

• Weisstein, Eric W. Hypohamiltonian Graph (англ.) на сайте Wolfram MathWorld.