Гипотеза Сингмастера — утверждение о том, что в треугольнике Паскаля имеется конечная верхняя граница количества одинаковых чисел, бо́льших единицы.
Гипотеза Эрдёша об арифметических прогрессиях — предположение в аддитивной комбинаторике, сформулированное Палом Эрдёшем, согласно которому в случае, если сумма обратных величин положительных натуральных чисел некоторого множества расходится, то множество содержит сколь угодно длинные арифметические прогрессии.
Гипотеза Кэмерона — Эрдёша — доказанная в 2003 году комбинаторная гипотеза.
В аналитической теории чисел функцией Дикмана ρ называется специальная функция, используемая для оценки числа гладких чисел для заданной границы. Впервые функция появилась у Карла Дикмана, в его единственной статье, посвященной математике. Позже функция была изучена датским математиком Николасом де Брёйном.
Европейский математический конгресс — крупнейшая европейская конференция, посвящённая математике; проводится раз в 4 года под эгидой Европейского математического общества. Первый конгресс прошёл в Париже в 1992 году. Доклады на конгрессе делятся на пленарные и секционные.
Гипотеза Келлера — выдвинутая Отт-Генрихом Келлером гипотеза о том, что в любой мозаике в евклидовом пространстве, состоящей из одинаковых гиперкубов, найдутся два куба, соприкасающиеся грань-к-грани. Например, как показано на рисунке, в любой мозаике на плоскости из одинаковых квадратов какие-то два квадрата должны соприкасаться ребро-к-ребру. Перрон доказал, что это верно в размерностях до 6; Бракензик с соавторами доказали верность гипотезы для размерности 7. Однако для бо́льших размерностей это неверно, как показали Лагариас и Шор для размерностей 10 и выше, Макей для размерностей 8 и выше, для чего использовали переформулировку задачи в терминах кликового числа некоторых графов, известных теперь как графы Келлера.
Гипотеза Барнетта — нерешённый вопрос в теории графов о существовании гамильтоновых циклов в графах. Гипотеза названа именем Дэвида В. Барнетта, эмерита калифорнийского университета в Дейвисе. Гипотеза утверждает, что любой двудольный граф многогранника с тремя рёбрами в каждой вершине имеет гамильтонов цикл.
Циклический порядок — способ упорядочивания объектов таким образом, чтобы последовательное движение по порядку после полного обхода совокупности возвращалось на начальный объект движения; полный порядок, «соединённый концами» в цикл. В отличие от структур, изучаемых в теории порядков, такой порядок не моделируется бинарным отношением, таким как «a < b», например, нельзя сказать, что восток «больше по часовой стрелке», чем запад; вместо этого циклический порядок определяется как тернарное отношение [a, b, c], означающее, что «после a достигается b раньше, чем c». Например, [Июнь, Октябрь, Февраль]. Тернарное отношение 
называется циклическим порядком, если оно является циклическим, асимметричным, транзитивным и полным. Порядок, не обладающий всеми этими свойствами, кроме полноты, называется частичным циклическим порядком.
Фальшивая проективная плоскость — это одна из 50 комплексных алгебраических поверхностей, которые имеют те же числа Бетти, что и у проективной плоскости, но не гомеоморфны ей. Такие объекты всегда являются алгебраическими поверхностями общего вида.
Гипотеза Фирузбэхт — это гипотеза о распределении простых чисел. Гипотеза носит имя иранского математика Фариды Фирузбэхт (1962—2019) из университета в Исфахане, которая высказала её в 1982 году.
Гипотеза Эрдёша — Фабера — Ловаса — это проблема о раскраске графов, названная именами Пала Эрдёша, Ванса Фабера и Ласло Ловаса, которые сформулировали её в 1972 году. Гипотеза гласит:
- Если k полных графов, каждый из которых имеет в точности k вершин, обладают свойством, что любая пара полных графов имеет не более одной общей вершины, то объединение графов может раскрашено в k цветов.
Сергей Александрович Степанов — советский и российский математик, работающий над теорией чисел, лауреат Государственной премии СССР (1975), доктор физико-математических наук (1977), доцент (1991), профессор кафедры фундаментальной и прикладной математики Института информационных наук и технологий безопасности РГГУ, член Американского математического общества. В работе 1969 года он использовал элементарные методы гипотезы Римана для дзета-функций гиперэлиптических кривых над конечными полями, ранее доказанных Андре Вейлем в 1940—1941 годах.
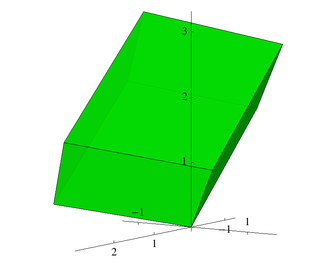
Дискриминант алгебраического числового поля — это числовой инвариант, который, грубо говоря, измеряет размер алгебраического числового поля. Более конкретно, он пропорционален квадрату объёма фундаментальной области кольца целых чисел и он определяет, какие простые числа разветвляются.
Генри Манн (1905—2000) — австрийский и американский математик еврейского происхождения. В 1946 году получил премию Коула.
Группа Тейта — Шафаревича — математическое понятие, используемое в диофантовой, алгебраической геометрии и алгебраической теории чисел. Независимо введено в совместной работе С. Ленга, Дж. Тейта и И. Р. Шафаревича.
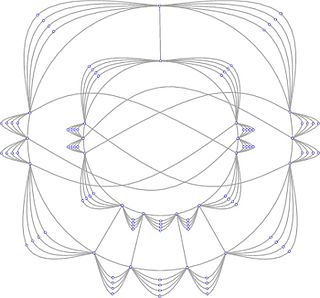
Топологический граф — представление графа на плоскости, в котором вершины графа представлены различными точками, а рёбра кривыми Жордана, соединяющими соответствующие пары точек. Точки, представляющие вершины графа, и дуги, представляющие рёбра, называются вершинами и рёбрами топологического графа. Обычно предполагается, что любые два ребра топологического графа пересекаются конечное число раз, при этом ни одно ребро не проходит через вершину и никакие два ребра не касаются друг друга. Топологический граф называется также «рисунком» графа.
Теорема Ханани — Татта — утверждение относительно чётности пересечений рёбер в визуализации графа. Теорема утверждает, что любой рисунок непланарного графа на плоскости содержит пару независимых рёбер, которые пересекают друг друга нечётное число раз. Эквивалентно, утверждение может быть переформулировано как критерий планарности — граф планарен тогда и только тогда, когда он имеет рисунок, в котором каждая пара независимых рёбер пересекается чётное число раз.
![{\displaystyle [n+1,n+k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3466c4d996bc7073045fc4c418c0bd9127e2c3a)
