Гипотеза Тэйта (теория графов)

Перейти к навигацииПерейти к поиску

Гипотеза Тэйта — опровергнутая математическая гипотеза о том, что любой 3-связный планарный кубический граф имеет гамильтонов цикл, проходящий через все его вершины.

Высказана в 1884 году Питером Тэйтом[1], опровергнута в 1946 году Уильямом Таттом[2], который построил контрпример с 25 гранями, 69 рёбрами и 46 вершинами — граф Татта. Позднее, в 1988 году, найден контрпример с 21 гранями, 57 рёбрами и 38 вершинами и доказано, что этот граф минимален[3].

Условие 3-регулярности (3-регулярные графы называются кубическими) необходимо, поскольку существуют многогранники, такие как ромбододекаэдр. Ромбододекаэдр образует двудольный граф и любой гамильтонов цикл в этом графе должен поочерёдно менять доли (стороны) графа, так что число вершин в долях должно быть равно, однако граф имеет шесть вершин степени 4 на одной стороне и восемь вершин степени 3 на другой.

Если бы гипотеза была верна, то из неё следовало бы простое решение проблемы четырёх красок. Согласно Тэйту, задача четырёх красок эквивалентна задаче поиска рёберной 3-раскраски кубических планарных графов без мостов. В гамильтоновом кубическом планарном графе такую раскраску рёбер легко найти — поочерёдно используем два цвета для раскраски рёбер вдоль гамильтонова цикла, а третьим цветом выкрасим оставшиеся рёбра. Альтернативно можно построить раскраску в четыре цвета граней гамильтонова кубического планарного графа прямо, если использовать два цвета для раскраски граней внутри цикла и два цвета для граней снаружи.

Контрпример Татта

Фрагмент Татта

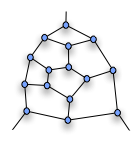
Ключом контрпримера является граф, называемый теперь фрагментом Татта. Если этот фрагмент является частью большего графа, любой гамильтонов цикл должен проходить через (висячее) ребро при верхней вершине (и через одно из нижних рёбер). Путь не может войти через нижнее ребро и выйти через другое нижнее ребро.

Контрпример Татта — три фрагмента Татта, соединённые в центре

Фрагмент Татта используется для построения негамильтонова графа Татта, если сложить вместе три таких фрагмента. «Обязательные» рёбра фрагментов, которые обязаны быть частями гамильтонова пути через фрагмент, соединены в центре. Поскольку любой цикл может проходить только через два из трёх рёбер в центре, гамильтонова цикла для этого графа быть не может. Получившийся граф Татта является 3-связным и планарным, так что он является графом многогранника по теореме Штайница. Граф имеет 25 граней, 69 рёбер и 46 вершин. Геометрически граф можно получить из тетраэдра (грани которого соответствуют четырём большим граням на рисунке — три грани между парами фрагментов, а четвёртая грань является внешней) путём многократного усечения трёх его вершин.

Меньшие контрпримеры

Как показали Холтон и Маккей в 1988 году[3], существует ровно шесть негамильтоновых 3-регулярных многогранников с 38 вершинами. Многогранники образованы заменой двух вершин пятиугольной призмы тем же фрагментом из примера Татта.

См. также

  • Теорема Гринберга — необходимое условие существования гамильтонова цикла, которое можно использовать, чтобы показать, что граф является контрпримером гипотезе Тэйта.
  • Гипотеза Барнетта — остающееся открытым усовершенствование гипотезы Тэйта; гипотеза утверждает, что любой двудольный кубический полиэдральный граф является гамильтоновым.[4]

Примечания

  1. ↑ Tait, 1884.
  2. ↑ Tutte, 1946.
  3. ↑ 1 2 Holton, McKay, 1988.
  4. ↑ Barnette’s conjecture Архивная копия от 14 декабря 2021 на Wayback Machine, the Open Problem Garden, retrieved 2009-10-12.

Литература

  • D. A. Holton, B. D. McKay. The smallest non-Hamiltonian 3-connected cubic planar graphs have 38 vertices // Journal of Combinatorial Theory, Series B. — 1988. — Т. 45, вып. 3. — С. 305–319. — doi:10.1016/0095-8956(88)90075-5.
  • P. G. Tait. Listing's Topologie // Philosophical Magazine (5th ser.). — 1884. — Т. 17. — С. 30–46. Статья перепечатана в Scientific Papers, том II, стр. 85-98.
  • W. T. Tutte. On Hamiltonian circuits // Journal of the London Mathematical Society. — 1946. — Т. 21, вып. 2. — С. 98–101. — doi:10.1112/jlms/s1-21.2.98.

Ссылки