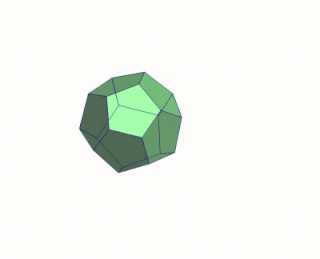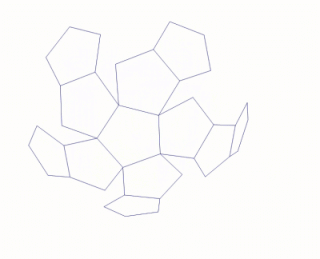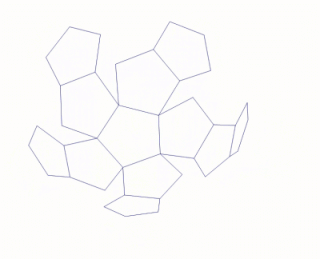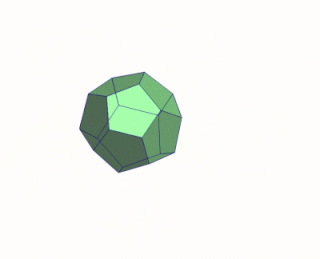
Развёртка многогранника — совокупность многоугольников, соответственно равных граням многогранника, с указанием того, какие стороны и вершины многоугольников соответствуют одним и тем же рёбрам и вершинам многогранника. Модели многогранников часто склеиваются из развёрток или отдельных многоугольников с указанием сторон, которые должны быть склеены.

Выпуклый многогранник — многогранник, являющийся выпуклым множеством. Это основное понятие в задачах линейного программирования.
Премия Фалкерсона — научная награда за выдающиеся работы в области дискретной математики, вручаемая совместно Обществом математической оптимизации (MOS) и Американским математическим обществом (AMS) на международном симпозиуме MOS, который проходит раз в три года. На каждом таком мероприятии объявляется более трёх номинаций, каждая из которых может включать нескольких учёных. Размер премии — полторы тысячи долларов, изначально выплачивалась из фонда, организованного друзьями Делберта Рея Фалкерсона после его смерти для поддержки математических работ в его области.

Полиэдральный граф — неориентированный граф, образованный из вершин и рёбер выпуклого многогранника, или, в контексте теории графов — вершинно 3-связный планарный граф.
Комбинаторика многогранников — это область математики, принадлежащая комбинаторике и комбинаторной геометрии и изучающая вопросы подсчёта и описания граней выпуклых многогранников.

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.
Правильный косой многогранник — это обобщение множества правильных многогранников, которое включает возможность непланарных граней или вершинных фигур. Коксетер рассматривал косые вершинные фигуры, которые создавали новые четырёхмерные правильные многогранники, а много позднее Бранко Грюнбаум рассматривал правильные косые грани.

Задача об иголке состоит в определении минимальной площади фигуры на плоскости, в которой единичный отрезок, «иглу», можно развернуть на 180 градусов, вернув его в исходное положение с обращённой ориентацией. Такое возможно проделать в круге радиуса 1/2. Другой пример — фигура, ограниченная дельтоидой, — показан на картинке, он имеет меньшую площадь.
Экзотическая сфера — гладкое многообразие М, которое гомеоморфно, но не диффеоморфно стандартной n-сфере.

В пятимерной геометрии пятимерный многогранник или 5-многогранник — это многогранник в пространстве размерности 5, ограниченный 4-мерными гранями. При этом каждая 3-мерная многогранная ячейка принадлежит ровно двум 4-мерным граням.

Многогранники Ханнера — класс выпуклых многогранников, которые можно получить рекурсивно из отрезка при помощи двух операций: взятие прямого произведения и переход к двойственному многограннику.
3d-гипотеза Калая — гипотеза о минимальном числе граней у центрально-симметричных многогранников. Сформулирована Калаем в 1989 году.

Ребро в геометрии — отрезок, соединяющий две вершины многоугольника или многогранника. В многоугольниках ребро является отрезком, лежащим на границе и чаще называется стороной многоугольника. В трёхмерных многогранниках и в многогранниках большей размерности ребро — это отрезок, общий для двух граней. Отрезок, соединяющий две вершины и проходящий через внутренние или внешние точки, ребром не является и называется диагональю.
Кривая моментов — алгебраическая кривая в d-мерном евклидовом пространстве, заданная множеством точек с декартовыми координатами


Франсиско Сантос Леал — испанский математик, известен своим контрпримером к гипотезе Хирша в многогранной комбинаторике. За это открытие был награждён премией Фалкерсона. В 2013 году награждался премией Гумбольдта.

Операция snub или отсечение вершин — это операция, применяемая к многогранникам. Термин появился из названий, данных Кеплером двум архимедовым телам — плосконосый куб и плосконосый додекаэдр. В общем случае плосконосые формы имеют хиральную симметрию двух видов, с ориентацией по часовой стрелке и против часовой стрелки. Согласно названиям Кеплера, отсечение вершин можно рассматривать как растяжение правильного многогранника, когда исходные грани отодвигаются от центра и поворачиваются относительно центров, вместо исходных вершин добавляются многоугольники с центрами в этих вершинах, а пары треугольников заполняют пространство между исходными рёбрами.
k-Смежностный многогранник — это выпуклый многогранник, в котором любое k-элементное подмножество его вершин является множеством вершин некоторой грани этого многогранника.
Асимптотическая размерность метрического пространства — аналог размерности Лебега на большой шкале. Асимптотическая размерность имеет важные приложения в геометрическом анализе и теории индексов.


















