Второ́й зако́н Нью́то́на — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона. Основной закон динамики.
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
И́мпульс — векторная физическая величина, являющаяся мерой механического движения тела.
Уравне́ние Шрёдингера — линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах.
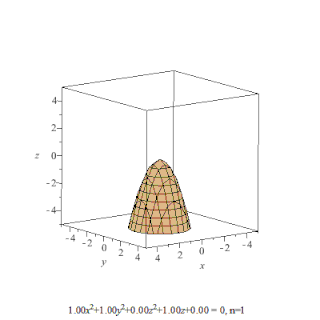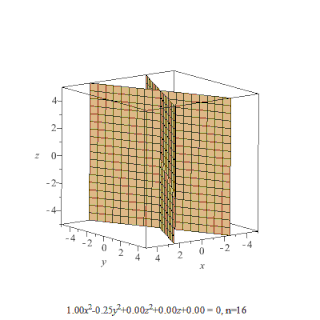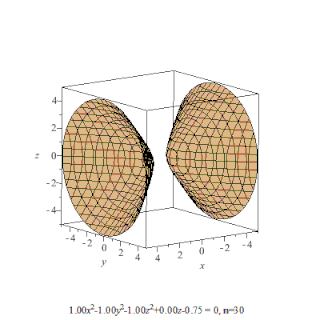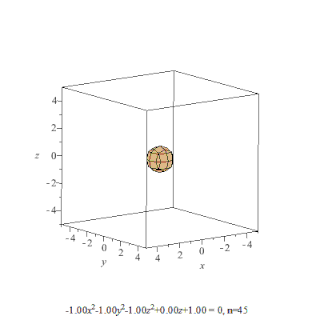
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида

Уравне́ния Гамильто́на в физике и математике — система дифференциальных уравнений:



Траекто́рия материа́льной то́чки — линия в пространстве, по которой движется тело, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения.

Поде́ра кривой относительно точки — некоторая кривая, составленная из оснований перпендикуляров, опущенных из данной точки на касательные к данной кривой.
Механической связью называют ограничения, накладываемые на координаты и скорости механической системы, которые должны выполняться на любом её движении. Связь можно описать математически как равенство или неравенство, содержащее время, координаты и скорости.
В классической механике уравне́ния Аппе́ля рассматривают как альтернативную формулировку общих уравнений движения, предложенных Ньютоном. Выписаны Полем Аппелем в 1900 . Несмотря на то, что эти уравнения полностью эквивалентны уравнениям, получаемым из законов Ньютона и принципа наименьшего действия, уравнения Аппеля в ряде случаев оказываются более удобными, в частности, в случае, когда система стеснена механическими связями.
Действие в физике — скалярная физическая величина, являющаяся мерой движения физической системы. Действие является математическим функционалом, который берёт в качестве аргумента траекторию движения физической системы и возвращает в качестве результата вещественное число.
Неголономная система — механическая система, на которую, кроме геометрических, накладываются и кинематические связи, которые нельзя свести к геометрическим. Математически неголономные связи выражаются неинтегрируемыми уравнениями. Движение неголономной системы описывается с помощью специальных уравнений движения или уравнений движения, получаемых из вариационных принципов.

Статистическая механика или статистическая термодинамика — механика больших ансамблей относительно простых систем, таких как атомы в кристалле, молекулы в газе, фотоны в лазерном пучке, звёзды в галактике, автомобили на шоссе. Статистическая механика использует статистические методы для определения свойств и поведения макроскопических физических систем, находящихся в термодинамическом равновесии, на основе их микроскопической структуры и законов движения, которые считаются заданными. Статистические методы были введены в этом контексте Максвеллом в серии из трех статей (1860—1879) и Больцманом в серии из четырёх статей (1870—1884), которые заложили основы кинетической теории газов. Классическая статистическая механика была основана Гиббсом (1902); а позднее описание микроскопических состояний на основе классической механики было исправлено и дополнено в соответствии с квантовой механикой. Термодинамика, кинетическая теория и статистическая механика — это дисциплины, связанные объектом исследования, но отличающиеся используемыми методами; часто они представлены вместе под общим названием статистической физики. Последовательное построение неравновесной статистической механики было выполнено Н. Н. Боголюбовым в 1946 году. При описании систем в рамках статистической механики используется понятие среднего по ансамблю. Основными уравнениями статистической механики являются уравнения Лиувилля и цепочка уравнений Боголюбова.
Голоно́мная связь — механическая связь, налагающая ограничения только на положения точек и тел системы.
При́нцип возмо́жных перемеще́ний — один из вариационных принципов в теоретической механике, устанавливающий общее условие равновесия механической системы. Согласно этому принципу, для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма виртуальных работ  только активных сил на любом возможном перемещении системы была равна нулю.
только активных сил на любом возможном перемещении системы была равна нулю.
Обобщённые координаты — переменные состояния системы, описывающие конфигурацию динамической системы относительно некоторой эталонной конфигурации в аналитической механике, а конкретно исследовании динамики твёрдых тел в системе многих тел. Эти переменные должны однозначно определять конфигурацию системы относительно эталонной конфигурации. Обобщённые скорости — производные по времени обобщённых координат системы.

H-принцип — общий способ решения дифференциальных уравнений в частных производных и, в более общем плане, дифференциальных соотношений в частных производных. Н-принцип хорош для недоопределённых систем, подобных тем, которые появляются в задачах о погружении, изометрическом погружении и других.
Теорема об изменении кинетического момента системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает изменение кинетического момента с моментом внешних сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь в теореме, может выступать любая механическая система, состоящая из любых тел.
В классической механике уравнение Удвадия — Калабы представляет собой метод получения уравнений движения механической системы с ограничениями (связями). Уравнение было впервые получено Фирдаусом Э. Удвадия и Робертом Э. Калабой в 1992 году. Подход основан на принципе наименьшего принуждения Гаусса. Уравнение Удвадия — Калабы применимо к широкому классу связей, как голономных, так и неголономных, если они линейны относительно ускорений. Уравнение также можно обобщить на связи, которые не подчиняются принципу Даламбера.






















