Фундамента́льная гру́ппа — одна из простейших конструкций в алгебраической топологии. Сопоставляется группа всякому связному топологическому пространству. Для подмножеств плоскости эта группа измеряет количество «дырок». Наличие «дырки» определяется невозможностью непрерывно продеформировать (стянуть) некоторую замкнутую кривую в точку.

В математике, если заданы две группы (G, ∗) и (H, •), гомоморфизм групп из (G, ∗) в (H, •) — это функция h : G → H, такая, что для всех u и v из G выполняется

Гру́ппа — множество, на котором определена ассоциативная бинарная операция, причём для этой операции имеется нейтральный элемент, и каждый элемент множества имеет обратный. Раздел общей алгебры, занимающийся группами, называется теорией групп.
Циклическая группа — группа  , которая может быть порождена одним элементом a, то есть все её элементы являются степенями a. Математическое обозначение:
, которая может быть порождена одним элементом a, то есть все её элементы являются степенями a. Математическое обозначение:  .
.
Изоморфизм групп — взаимно-однозначное соответствие между элементами двух групп, сохраняющее групповые операции. Если существует изоморфизм между двумя группами, группы называются изоморфными. С точки зрения теории групп изоморфные группы имеют одни и те же свойства и их можно не различать.
Теория групп — раздел общей алгебры, изучающий алгебраические структуры, называемые группами, и их свойства. Группа является центральным понятием в общей алгебре, так как многие важные алгебраические структуры, такие как кольца, поля, векторные пространства, являются группами с расширенным набором операций и аксиом. Группы возникают во всех областях математики, и методы теории групп оказывают сильное влияние на многие разделы алгебры. В процессе развития теории групп построен мощный инструментарий, во многом определивший специфику общей алгебры в целом, сформирован собственный глоссарий, элементы которого активно заимствуются смежными разделами математики и приложениями. Наиболее развитые ветви теории групп — линейные алгебраические группы и группы Ли — стали самостоятельными областями математики.
Гиперболическая группа — конечно-порождённая группа, граф Кэли которой, как метрическое пространство, является гиперболическим по Громову.
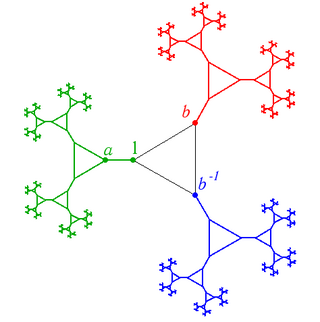
Свободным произведением групп называется группа, порождённая элементами этих двух групп, без каких-либо дополнительных соотношений.

Решётка — набор векторов евклидова пространства  , образующий дискретную группу по сложению.
, образующий дискретную группу по сложению.
Бесконечная группа — группа с бесконечным числом элементов, в противоположность конечным группам. Первое исследование бесконечных групп восходит к Жордану (1870).
В общей алгебре, термин кручение относится к элементам группы, имеющим конечный порядок, или к элементам модуля, аннулируемым регулярным элементом кольца.
В математике свободная абелева группа — это абелева группа, имеющая базис, то есть такое подмножество элементов группы, что для любого её элемента существует единственное его представление в виде линейной комбинации базисных элементов с целыми коэффициентами, из которых только конечное число являются ненулевыми. Элементы свободной абелевой группы с базисом B называют также формальными суммами над B. Свободные абелевы группы и формальные суммы используются в алгебраической топологии при определении групп цепей и в алгебраической геометрии при определении дивизоров.
Тест ассоциативности — проверка бинарной операции на ассоциативность. Наивная процедура проверки, заключающаяся в переборе всех возможных троек аргументов операции, требует  времени, где
времени, где  — размер множества, над которым определена операция. Ранние тесты ассоциативности не давали асимптотических улучшений по сравнению с наивным алгоритмом, однако позволяли улучшить время работы в некоторых частных случаях. Например, Роберт Тарьян в 1972 году обнаружил, что предложенный в 1949 году тест Лайта позволяет выполнить проверку за
— размер множества, над которым определена операция. Ранние тесты ассоциативности не давали асимптотических улучшений по сравнению с наивным алгоритмом, однако позволяли улучшить время работы в некоторых частных случаях. Например, Роберт Тарьян в 1972 году обнаружил, что предложенный в 1949 году тест Лайта позволяет выполнить проверку за  , если исследуемая бинарная операция обратима. Первый вероятностный тест, улучшающий время работы с
, если исследуемая бинарная операция обратима. Первый вероятностный тест, улучшающий время работы с  до
до  , был предложен в 1996 году Шридхаром Раджагопаланом и Леонардом Шульманом. В 2015 году был предложен квантовый алгоритм, проверяющий операцию на ассоциативность за время
, был предложен в 1996 году Шридхаром Раджагопаланом и Леонардом Шульманом. В 2015 году был предложен квантовый алгоритм, проверяющий операцию на ассоциативность за время  , что является улучшением по сравнению с поиском Гровера, работающим за
, что является улучшением по сравнению с поиском Гровера, работающим за  .
.
Лампочная группа — группа, определённым образом описывающая деятельность фонарщика. Также используются названия группа мигающих лампочек и группа фонарщика.
 Граф Кэли свободной группы с двумя образующими a и b
Граф Кэли свободной группы с двумя образующими a и b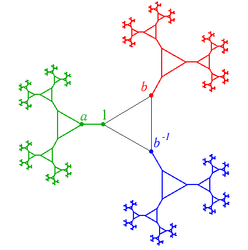 Граф Кэли свободного произведения
Граф Кэли свободного произведения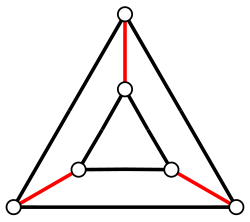 Граф Кэли прямого произведения
Граф Кэли прямого произведения



































