Граф Фостера
| Граф Фостера | |
|---|---|
 | |
| Назван в честь | Рональда Фостера |
| Вершин | 90 |
| Рёбер | 135 |
| Радиус | 8 |
| Диаметр | 8 |
| Обхват | 10 |
| Автоморфизмы | 4320 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Свойства | кубический дистанционно-транзитивный |
Граф Фостера — двудольный 3-регулярный граф с 90 вершинами и 135 рёбрами[1]. Граф Фостера является гамильтоновым, имеет хроматическое число 2, хроматический индекс 3, радиус 8, диаметр 8 и обхват 10. Также является вершинно 3-связным и рёберно 3-связным.
Все кубические дистанционно-регулярные графы известны[2], граф Фостера — один из 13 таких графов. Граф является единственным дистанционно-транзитивным графом с массивом пересечений {3,2,2,2,2,1,1,1;1,1,1,1,2,2,2,3}[3]. Граф можно построить как граф инциденций частично линейного пространства[англ.], которое является единственным тройным накрытием без восьмиугольников обобщённых четырёхугольников GQ (2,2). Граф назван в честь Рональда Фостера, составившего список кубических симметричных графов (список Фостера), который включает граф Фостера.
Алгебраические свойства
Группа автоморфизмов графа Фостера — это группа порядка 4320[4]. Она действует транзитивно на вершины и рёбра графа, поэтому граф Фостера является симметричным. Граф имеет автоморфизмы, которые переводят любую вершину в любую другую и любое ребро в любое другое ребро. В списке Фостера граф Фостера, указанный как F90A, является единственным кубическим симметричным графом с 90 вершинами[5].
Характеристический многочлен графа Фостера равен .
Галерея
 Граф Фостера, раскрашенный таким образом, чтобы выделить различные циклы.
Граф Фостера, раскрашенный таким образом, чтобы выделить различные циклы.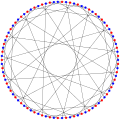 Хроматическое число графа Фостера равно 2.
Хроматическое число графа Фостера равно 2.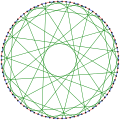 Хроматический индекс графа Фостера равен 3.
Хроматический индекс графа Фостера равен 3.
Примечания
- ↑ Weisstein, Eric W. Foster Graph (англ.) на сайте Wolfram MathWorld.
- ↑ A. E. Brouwer, A. M. Cohen, A. Neumaier. Distance — Regular Graphs. — New York: Springer—Verlag, 1989.
- ↑ Cubic distance-regular graphs Архивная копия от 1 июля 2014 на Wayback Machine, A. Brouwer.
- ↑ Royle, G. F090A data (недоступная ссылка)
- ↑ M. Conder, P. Dobcsányi, «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41—63, 2002.
Литература
- N. L. Biggs, A. G. Boshier, J. Shawe—Taylor. Cubic distance — regular graphs // Journal of the London Mathematical Society. — 1986. — Т. 33, вып. 3. — С. 385—394. — doi:10.1112/jlms/s2-33.3.385.
- Edwin R. Van Dam, Willem H. Haemers. Spectral characterizations of some distance — regular graphs // Journal of Algebraic Combinatorics. — 2002. — Т. 15, вып. 2. — С. 189—202. — doi:10.1023/A:1013847004932.
- Hendrik Van Maldeghem. Ten exceptional geometries from trivalent distance regular graphs // Annals of Combinatorics. — 2002. — Т. 6, вып. 2. — С. 209—228. — doi:10.1007/PL00012587.



















