Граф Хершеля

Граф Хершеля
Назван в честь	А. С. Хершель[англ.]
Вершин	11
Рёбер	18
Радиус	3
Диаметр	4
Обхват	4
Автоморфизмы	12 (D6)
Хроматическое число	2
Хроматический индекс	4
Свойства	полиэдральный планарный двудольный совершенный
Медиафайлы на Викискладе

В теории графов граф Хершеля — это двудольный неориентированный граф с 11 вершинами и 18 рёбрами, наименьший негамильтонов полиэдральный граф. Граф назван по имени британского астронома А. С. Хершеля^[англ.], написавшего раннюю работу по поводу игры «Икосиан» Уильяма Роуэна Гамильтона — граф Хершеля даёт наименьший выпуклый многогранник, для которого игра не имеет решения. Однако статья Хершеля описывает решения для игры «Икосиан» только для тетраэдра и икосаэдра, и не описывает граф Хершеля^[1].

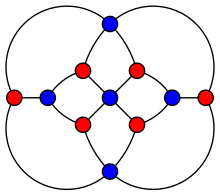
Граф Хершеля планарен — его можно нарисовать на плоскости без пересечения рёбер. Он также вершинно 3-связен — удаление любых двух вершин оставляет подграф связным. Поэтому, по теореме Штайница граф Голднера — Харари является полиэдральным графом — существует выпуклый многогранник (эннеаэдр), имеющий граф Хершеля в качестве своего скелета^[2]. Граф Хершеля является также двудольным — его вершины можно разбить на два подмножества из пяти и шести вершин так, что каждое ребро имеет конечные вершины в обоих множествах (красные и синие подмножества на рисунке).

Как и любой другой двудольный граф, граф Хершеля является совершенным — хроматическое число любого порождённого подграфа равно размеру наибольшей клики этого подграфа. Граф имеет хроматический индекс 4, обхват 4, радиус 3 и диаметр 4.

Поскольку граф является двудольным и имеет нечётное число вершин, он не содержит гамильтонов цикл (цикл из рёбер, который проходит через каждую вершину в точности один раз). В любом двудольном графе любой цикл должен попеременно проходить оба множества вершин, а потому, должен содержать равное число вершин обоих типов и иметь чётную длину. Таким образом, цикл, проходящий через каждую из одиннадцати вершин, существовать не может. Граф является минимальным негамильтоновым полиэдральным графом, как бы ни измерялся размер графа — по числу вершин, рёбер или граней^[3]. Существует другой полиэдральный граф с 11 вершинами, не имеющий гамильтоновых циклов (а именно, граф Голднера — Харари^[4]), но нет графа с меньшим (либо равным) числом рёбер^[2].

Все вершины графа Хершеля, за исключением трёх, имеют степень три. Гипотеза Тейта^{[англ.][5]} утверждает, что полиэдральный граф, в котором любая вершина имеет степень три должен быть гамильтоновым, но она опровергнута контрпримером, который привёл Татт, много большим графом Татта^[6]. Обновление гипотезы Татта, гипотеза Барнетте^[англ.], что любой двудольный 3-регулярный полиэдральный граф является гамильтоновым, остаётся открытой^[7].

Граф Хершеля даёт также пример полиэдрального графа, для которого срединный граф не может быть разбит на два непересекающихся по рёбрам гамильтонова цикла. Серединным графом графа Хершеля является 4-регулярный граф с 18 вершинами, по одной для каждого ребра графа Хершеля. Две вершины смежны в срединном графе, если соответствующие рёбра графа Хершеля идут последовательно на одной из его граней^[8].

Граф Хершеля не вершинно-транзитивен и его полная группа автоморфизмов изоморфна диэдрической группе 12 порядка, группе симметрий правильного шестиугольника, включающей как вращения, так и отражения. Любую перестановку его вершин четвёртой степени можно представить автоморфизмом графа, и существует ещё нетривиальный автоморфизм, переставляющий оставшиеся вершины, не затрагивая вершины четвёртой степени.

Характеристический многочлен графа Хершеля равен ${\displaystyle -x^{3}(x^{2}-11)(x^{2}-3)(x^{2}-2)^{2}}$.

• Weisstein, Eric W. Herschel Graph (англ.) на сайте Wolfram MathWorld.