Граф Холла — Янко

Перейти к навигацииПерейти к поиску
Граф Холла — Янко
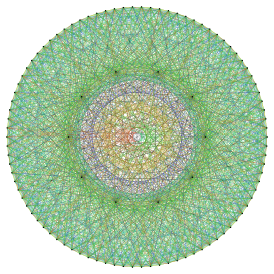HJ как граф Фостера (90 внешних вершин) плюс система Штейнера S(3,4,10) (10 внутренних вершин).
HJ как граф Фостера (90 внешних вершин) плюс система Штейнера S(3,4,10) (10 внутренних вершин).
Назван в честьЗвонимир Янко
Маршал Холл
Вершин 100
Рёбер 1800
Радиус 2
Диаметр 2
Обхват 3
Автоморфизмы 1209600
Хроматическое число 10
Свойствасильно регулярный
вершинно транзитивен
граф Кэли
эйлеров
гамильтонов
целый
Логотип Викисклада Медиафайлы на Викискладе

Граф Холла — Янко, также называемый графом Холла — Янко — Уэлса, это 36-регулярный неориентированный граф со 100 вершинами и 1800 рёбрами[1].

Граф имеет ранг 3 и является сильно регулярным графом с параметрами (100,36,14,12) и наибольшей кокликой[2] размера 10. Это множество параметров не уникально, однако однозначно определено параметрами как графа ранга 3. Граф Холла — Янко первоначально построил Д. Уэлс для установления существования группы Холла — Янко как подгрупп индекса 2 его группы автоморфизмов.

Граф Холла — Янко можно построить из объектов U3(3), простой группы порядка 6048[3][4]:

  • В U3(3) имеется 36 простых максимальных подгрупп порядка 168. Они будут вершинами подграфа, U3(3) графа. 168-Подгруппа имеет 14 максимальных подгрупп порядка 24, изоморфных S4. Две 168-подгруппы считаются смежными, если они пересекаются по 24-подгруппе. Граф U3(3) является строго регулярным графом с параметрами (36,14,4,6)
  • Имеется 63 инволюции (элементов порядка 2). 168-Подгруппа содержит 21 инволюцию, которые считаются соседями.
  • Вне U3(3) пусть имеется 100-я вершина C, соседями которой являются 36 168-подгрупп. 168-подгруппа тогда имеет 14 общих соседей с C и 1+14+21 соседей всего.
  • Инволюция находится в 12 168-подгруппах. Вершина C и инволюция не смежны, но имеют 12 общих соседей.
  • Две инволюции считаются смежными, если они генерируют диэдральную подгруппу порядка 8[5]. Инволюция имеет 24 инволюции в качестве соседей.

Характеристический многочлен графа Холла — Янко равен . Таким образом, граф Холла — Янко является целым графом — его спектр состоит лишь из целых чисел.

Примечания

  1. ↑ Weisstein, Eric W. Hall-Janko graph (англ.) на сайте Wolfram MathWorld.
  2. ↑ Васильев, Вдовин, 2011, Множество вершин графа называется кокликой или независимым, если его вершины попарно несмежны., с. 425.
  3. ↑ Brouwer U3(3).
  4. ↑ Brouwer HJ graph.
  5. ↑ Wilson, 2009, с. 224.

Литература

  • Andries E. Brouwer. Hall-Janko graph.
  • Andries E. Brouwer. U3(3) graph.
  • Васильев А.В., Вдовин Е.П. Коклики максимального размера в графе простых чисел конечной простой группы // Алгебра и логика. — 2011. — Т. 50, вып. 4. — С. 425–470.
  • Robert A. Wilson. The Finite Simple Groups. — Springer-Verlag, 2009. — Т. 251. — (Graduate Text in Mathematics). — ISBN 978-1-84800-987-5.