В теории графов под графом Клебша понимается один из двух дополняющих друг друга графов, имеющих 16 вершин. Один из них имеет 40 рёбер и является 5-регулярным графом, другой имеет 80 рёбер и является 10-регулярным графом. 80-рёберный вариант — это половинный граф куба 5-го порядка. Назван графом Клебша в 1968 году Зайделем ввиду его связи с конфигурацией прямых поверхности четвёртого порядка, открытой 1868 году немецким математиком Альфредом Клебшем. 40-рёберный вариант – это складной граф куба 5 порядка. Он известен также под именем граф Гринвуда — Глизона после работы Гринвуда и Глизона, в которой они использовали этот граф для вычисления числа Рамсея R (3,3,3) = 17 .
В теории графов графом МакГи, или (3-7)-клеткой, называется 3-регулярный граф с 24 вершинами и 36 рёбрами.
В теории графов графом Паппа называется двудольный 3-регулярный неориентированный граф с 18 вершинами и 27 рёбрами, являющийся графом Леви конфигурации Паппа. Он назван в честь Паппа Александрийского, математика Древней Греции, который верил, что доказал «теорему о шестиугольнике», в которой описывал конфигурацию Паппа. Все кубические дистанционно-регулярные графы известны. Граф Паппа — один из тринадцати таких графов.
Граф Дика — 3-регулярный граф с 32 вершинами и 48 рёбрами, назван в честь Вальтера фон Дика .
Снарк Секереша — снарк с 50 вершинами и 75 рёбрами, пятый известный снарк. Открыт Дьёрдьем Секерешем в 1973 году.
Граф Биггса — Смита — 3-регулярный граф с 102 вершинами и 153 рёбрами. Назван в честь Биггса и Смита, описавших граф в 1971 году.
Граф Коксетера — 3-регулярный граф с 28 вершинами и 42 рёбрам Все кубические дистанционно-регулярные графы известны, граф Коксетера — один из 13-ти таких графов.
В теории графов граф Франклина — это 3-регулярный граф с 12 вершинами и 18 рёбрами.
Граф F26A — симметричный двудольный кубический граф с 26 вершинами и 39 рёбрами.
В теории графов граф Харриса или (3-10)-клетка Харриса — это 3-регулярный неориентированный граф с 70 вершинами и 105 рёбрами.
В теории графов граф Харриса — Вонга — это 3-регулярный неориентированный граф с 70 вершинами и 105 рёбрами.
Граф Хортона — 3-регулярный граф с 96 вершинами и 144 рёбрами, открытый Джозефом Хортоном. Бонди и Мурти опубликовали в 1976 этот граф в качестве контрпримера гипотезе Татта, что любой кубический 3-связный двудольный граф является гамильтоновым.
Алмаз — планарный неориентированный граф с 4 вершинами и 5 рёбрами. Граф представляет собой полный граф 
без одного ребра.
Граф Фолкмана — это двудольный 4-регулярный граф с 20 вершинами и 40 рёбрами.
11-клетка Балабана или (3-11)-клетка Балабана — это 3-регулярный граф с 112 вершинами и 168 рёбрами, названные именем румынского химика Александру Т. Балабана.
Граф Холта или граф Дойла является наименьшим полутранзитивным графом, то есть наименьшим примером вершинно-транзитивного и рёберно-транзитивного графа, который не является симметричным. Такие графы не часто встречаются. Граф назван именами Питера Дж. Дойла и Дерека Ф. Холта, обнаружившими граф независимо в 1976 и 1981 соответственно.
Граф Робертсона или (4,5)-клетка — это 4-регулярный неориентированный граф с 19 вершинами и 38 рёбрами, названный именем Нейла Робертсона.
Граф Мередита — 4-регулярный неориентированный граф с 70 вершинами и 140 рёбрами, обнаруженный Гаем Мередитом в 1973 году.
Алан Джером Хоффман — американский математик, сотрудник Исследовательского центра Т. Дж. Уотсона компании IBM. Редактор и основатель журнала англ. Linear Algebra and its Applications. Он внес вклад в комбинаторную оптимизацию и теорию собственных значений графов. Хоффман совместно с Робертом Синглтоном построил граф Хоффмана — Синглтона, который является уникальным графом Мура степени 7 и диаметра 2.
Медиафайлы на Викискладе
Граф Хоффмана гамильтонов.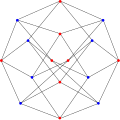
Хроматическое число графа Хоффмана равно 2.
Хроматический индекс графа Хоффмана равен 4.
