Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.
Признак Ди́ни — признак поточечной сходимости ряда Фурье. Несмотря на то, что ряд Фурье функции из 
сходится к ней в смысле 
-нормы, он вовсе не обязан сходиться к ней поточечно. Тем не менее при некоторых дополнительных условиях поточечная сходимость всё же имеет место.
Дискретное преобразование Фурье — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов, а также в других областях, связанных с анализом частот в дискретном сигнале.
Ортогона́льный (ортонорми́рованный) ба́зис — ортогональная (ортонормированная) система элементов линейного пространства со скалярным произведением, обладающая свойством полноты.
Z-преобразованием называют свёртывание исходного сигнала, заданного последовательностью вещественных чисел во временно́й области, в аналитическую функцию комплексной частоты. Если сигнал представляет импульсную характеристику линейной системы, то коэффициенты Z-преобразования показывают отклик системы на комплексные экспоненты 
, то есть на гармонические осцилляции с различными частотами и скоростями нарастания/затухания.
Фу́нкция Хевиса́йда — кусочно-постоянная функция, равная нулю для отрицательных значений аргумента и единице — для положительных. В нуле эта функция, вообще говоря, не определена, однако её обычно доопределяют в этой точке некоторым числом, чтобы область определения функции содержала все точки действительной оси. Чаще всего неважно, какое значение функция принимает в нуле, поэтому могут использоваться различные определения функции Хевисайда, удобные по тем или иным соображениям, например:
Экстраполятор нулевого порядка — математическая модель, использующаяся при цифро-аналоговом преобразовании для восстановления дискретизованного сигнала в аналоговой форме. Такая модель необходима из-за того, что цифровой сигнал записывается последовательностью дельта-функций xs(t), каждая из которых представляет собой один отсчёт дискретного сигнала x(nT), из которого восстанавливается непрерывный сигнал x(t). Однако использовать в качестве восстановленного сигнала последовательность импульсов непрактично и зачастую невозможно. Большинство современных цифро-аналоговых преобразователей выдают на выходе напряжение определённого уровня, которое сохраняется до следующего отсчёта.
Экстраполятор первого порядка — математическая модель для восстановления дискретизованного сигнала, которое может производиться обычным цифро-аналоговым преобразователем и аналоговой схемой (интегратором). В этом случае сигнал восстанавливается в виде кусочно-линейной аппроксимации изначально оцифрованного сигнала. По сравнению с экстраполятором нулевого порядка экстраполятор первого порядка в общем случае имеет меньший шум квантования и, следовательно, более точно восстанавливает сигнал.
Ядро Фейера — функция, применяющаяся для суммирования по Чезаро рядов Фурье или преобразований Фурье, задаваемая формулой:
,
Тригонометрический ряд Фурье — представление произвольной функции 
с периодом 
в виде ряда
В математике Дзета-функция Гурвица, названная в честь Адольфа Гурвица, — это одна из многочисленных дзета-функций, являющихся обобщениями дзета-функции Римана. Формально она может быть определена степенным рядом для комплексных аргументов s, при Re(s) > 1, и q, Re(q) > 0:
Интеграл Норлунда — Райса — интеграл, связывающий 
конечных разностей с криволинейным интегралом в комплексной плоскости. Интеграл используется в теории конечных разностей, а также в Информатике и теории графов для оценки длины двоичного дерева.
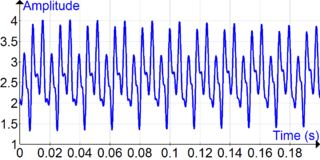
Анализ Фурье — направление в анализе, изучающее каким образом общие математические функции могут быть представлены либо приближены через сумму более простых тригонометрических функций. Анализ Фурье возник при изучении свойств рядов Фурье, и назван в честь Жозефа Фурье, который показал, что представление функции в виде суммы тригонометрических функций значительно упрощает изучение процесса теплообмена.
Спектральные методы — это класс используемых в прикладной математике методик для численного решения некоторых дифференциальных уравнений, иногда использующих Быстрое преобразование Фурье. Идея заключается в представлении решения дифференциальных уравнений как суммы некоторых «базисных функций» с последующим выбором коэффициентов в сумме, наиболее удовлетворяющих заданным уравнениям.
В теории многих тел термин функция Грина иногда используется как синоним корреляционной функции, но относится к корреляторам операторов поля или операторам рождения и уничтожения.
Теорема о свёртке гласит, что при подходящих условиях преобразование Фурье свёртки двух функций является поточечным произведением их преобразований Фурье. В более общем случае свёртка в одной области равна точечному умножению в другой области. Другие версии теоремы о свёртке применимы к различным преобразованиям Фурье.
