Коэффициент зацепления — целочисленная характеристика пары пространственных замкнутых кривых без пересечений и самопересечений, описывающая суммарное количество раз, которое одна кривая в определённом смысле зацепляется за другую.
Циклическая группа — группа  , которая может быть порождена одним элементом a, то есть все её элементы являются степенями a. Математическое обозначение:
, которая может быть порождена одним элементом a, то есть все её элементы являются степенями a. Математическое обозначение:  .
.
Теория узлов — изучение вложений одномерных многообразий в трёхмерное евклидово пространство или в сферу  . В более широком смысле предметом теории узлов являются вложения сфер в многообразия и вложения многообразий в целом.
. В более широком смысле предметом теории узлов являются вложения сфер в многообразия и вложения многообразий в целом.

В теории узлов трилистник — простейший нетривиальный узел. Трилистник можно получить, соединив 2 свободных конца обычного простого узла, в результате чего получаем заузленное кольцо. Как простейший узел, трилистник является фундаментальным объектом при изучении математической теории узлов, которая имеет многообразные приложения в топологии, геометрии, физике, химии и иллюзионизме.

Поверхность Зейферта — вложенная в трёхмерное пространство поверхность, краем которой является данный узел или зацепление. Названа в честь Герберта Зейферта и является полезным инструментом в теории узлов.
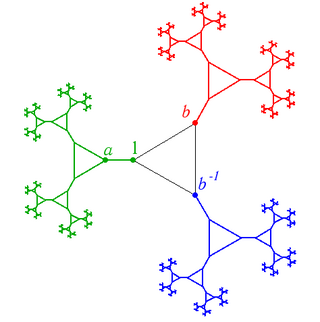
Свободным произведением групп называется группа, порождённая элементами этих двух групп, без каких-либо дополнительных соотношений.
Многочлен Джонса — полиномиальный инвариант узла, сопоставляющий каждому узлу или зацеплению многочлен Лорана от формальной переменной  с целыми коэффициентами. Построен Воном Джонсом в 1984 году.
с целыми коэффициентами. Построен Воном Джонсом в 1984 году.

Решётка — набор векторов евклидова пространства  , образующий дискретную группу по сложению.
, образующий дискретную группу по сложению.

Торический узел — специальный вид узлов, лежащих на поверхности незаузлённого тора в  .
.

В теории узлов прямой узел — это составной узел, полученный соединением трилистника с его отражением. Узел тесно связан с бабьим узлом, который также является соединением двух трилистников. Поскольку трилистник является простейшим нетривиальным узлом, прямой и бабий узлы являются простейшими составными узлами.

В теории узлов бабий узел — это составной узел, полученный соединением двух одинаковых трилистников. Узел тесно связан с прямым узлом, который тоже можно описать как соединение двух трилистников. Поскольку трилистник является простейшим нетривиальным узлом, прямой и бабий узлы являются простейшими составными узлами.
XTR — алгоритм шифрования с открытым ключом, основывающийся на вычислительной сложности задачи дискретного логарифмирования. Преимущества этого алгоритма перед другими, использующими эту идею, в более высокой скорости и меньшем размере ключа.

Модель Пуанкаре в верхней полуплоскости — это верхняя половина плоскости  , обозначаемая ниже как H, вместе с метрикой, которая делает её моделью двумерной гиперболической геометрии.
, обозначаемая ниже как H, вместе с метрикой, которая делает её моделью двумерной гиперболической геометрии.

Дополнение узла — пространство, получающееся из шара вырезанием цилиндра, заузленного в форме этого узла.
Абелианиза́ция — способ превратить произвольную группу в абелеву. Является полезным инструментом в теории групп, который находит применение в алгебраической топологии.

Теорема Артина о задании группы кос — фундаментальная теорема теории кос, предоставляющая комбинаторно-алгебраическую кодировку кос.

Группа трилистника — группа узла трилистника, простейшего нетривиального узла. Является классическим объектом изучения комбинаторной теории групп, который возникает в теории кос, алгебраической геометрии и алгебраической К-теории.


































