Фундамента́льная гру́ппа — одна из простейших конструкций в алгебраической топологии. Сопоставляется группа всякому связному топологическому пространству. Для подмножеств плоскости эта группа измеряет количество «дырок». Наличие «дырки» определяется невозможностью непрерывно продеформировать (стянуть) некоторую замкнутую кривую в точку.
Непреры́вное отображе́ние — отображение из одного пространства в другое, при котором близкие точки области определения переходят в близкие точки области значений.
В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глоссария.
Гомеоморфи́зм — непрерывная биекция с непрерывной обратной. Является центральным понятием топологии.
Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.
Диффеоморфизм — отображение определённого типа между гладкими многообразиями.
Ба́зис — упорядоченный набор векторов в векторном пространстве или модуле, такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора. Векторы базиса называются базисными векторами.
Ориента́ция — обобщение и формализация понятий направления обхода и направления на прямой на более сложные геометрические фигуры в пространстве, а также на сами пространства.
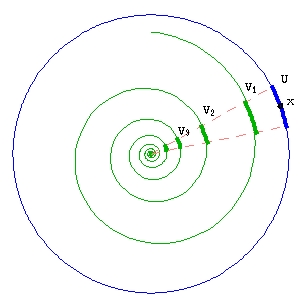
В теории динамических систем, теорема Пуанкаре о классификации гомеоморфизмов окружности описывает возможные типы обратимой динамики на окружности, в зависимости от числа вращения 
итерируемого отображения f. Грубо говоря, оказывается, что динамика итераций отображения в определённой степени похожа на динамику поворота на соответствующий угол.
Языки Арнольда — в теории динамических систем, области рациональности числа вращения в двупараметрическом семействе гомеоморфизмов окружности, начинающемся с чистых поворотов.
В математике, под группой Томпсона может пониматься:
- Конечная группа Томпсона, одна из спорадических конечных простых групп.
- Одна из бесконечных групп Томпсона F и T, являющихся подгруппами групп кусочно-линейных гомеоморфизмов отрезка и окружности соответственно.
Рациональная нормальная кривая — гладкая рациональная кривая степени n в n-мерном проективном пространстве 
Она является одним из сравнительно простых проективных многообразий, более формально, она является образом вложения Веронезе, применённого к проективной прямой.
Инверсия кривой — результат применения операции инверсии к заданной кривой C. По отношению к фиксированной окружности с центром O и радиусом k инверсия точки Q — это точка P, лежащая на луче OQ, и OP•OQ = k2. Инверсия кривой C — это множество всех точек P, являющихся инверсиями точек Q, принадлежащих кривой C. Точка O в этом построении называется центром инверсии, окружность называется окружностью инверсии, а k — радиусом инверсии.
В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.
Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
