Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре.
Плана́рный граф — граф, который можно изобразить на плоскости без пересечений рёбер не по вершинам. Какое-либо конкретное изображение планарного графа на плоскости без пересечения рёбер не по вершинам называется плоским графом. Иначе говоря, планарный граф изоморфен некоторому плоскому графу, изображённому на плоскости так, что его вершины — это точки плоскости, а рёбра — кривые на плоскости, которые если и пересекаются между собой, то только по вершинам. Области, на которые граф разбивает плоскость, называются его гранями. Неограниченная часть плоскости — тоже грань, называемая внешней гранью. Любой плоский граф может быть спрямлён, то есть перерисован на плоскости так, что все его рёбра будут отрезками прямых.
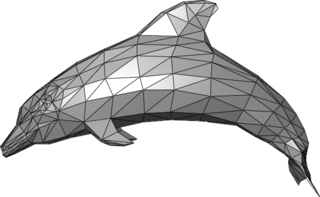
Полигональная сетка — это совокупность вершин, рёбер и граней, которые определяют форму многогранного объекта в трёхмерной компьютерной графике и объёмном моделировании. Гранями обычно являются треугольники, четырёхугольники или другие простые выпуклые многоугольники (полигоны), так как это упрощает рендеринг, но сетки могут также состоять и из наиболее общих вогнутых многоугольников[прояснить], или многоугольников с отверстиями.
Теорема Фа́ри — теоретико-графовое утверждение о возможности выпрямить рёбра любого планарного графа. Иными словами, разрешение рисовать рёбра не в виде отрезков, а в виде кривых, не расширяет класс планарных графов.

Вершинa графа — фундаментальное понятие теории графов. Неориентированный граф состоит из множества вершин и множества рёбер, в то время как ориентированный граф состоит из множества вершин и множества дуг. На рисунках, представляющих граф, вершина обычно обозначается кружком с меткой, ребро — линией, дуга — стрелкой, соединяющей вершины.

Полиэдральный граф — неориентированный граф, образованный из вершин и рёбер выпуклого многогранника, или, в контексте теории графов — вершинно 3-связный планарный граф.
Теорема Штайница — это комбинаторное описание неориентированных графов, образованных рёбрами и вершинами трёхмерного выпуклого многогранника — они в точности являются (простыми) вершинно 3-связными планарными графами. То есть любой выпуклый многогранник образует 3-связный планарный граф, и любой 3-связный планарный граф может быть представлен как выпуклый многогранник. По этой причине 3-связные планарные графы называют также полиэдральными.

Линк вершины многогранника или вершинная фигура — многогранник на единицу меньшей размерности, который получается в сечении исходного многогранника плоскостью, срезающей одну вершину. В частности линк вершины содержит информацию о порядке следования граней многогранника вокруг одной вершины.

Плосконосый додекаэдр, курносый додекаэдр или плосконосый икосододекаэдр — это полуправильный многогранник, одно из тринадцати выпуклых изогональных непризматических тел, гранями которых являются два или более правильных многоугольника.
Вершина — точка, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников.

В теории графов хорошо покрытый граф — это неориентированный граф, в котором все минимальные по включению вершинные покрытия имеют один и тот же размер. Хорошо покрытые графы определил и изучал Пламмер.

В теории графов outerplanar graph — это граф, допускающий планарную диаграмму, в которой все вершины принадлежат внешней грани.
Граф призмы — рёберный граф одной из призм.

Граф Аполлония — неориентированный граф, образованный рекурсивным процессом подразделения треугольника на три меньших треугольника. Графы Аполлония можно эквивалентно определить как планарные 3-деревья, как максимальные планарные хордальные графы, как однозначно 4-раскрашиваемые планарные графы или как графы блоковых многогранников. Графы названы именем Аполлония Пергского, изучавшего связанные построения упаковки кругов.

Ребро в геометрии — отрезок, соединяющий две вершины многоугольника или многогранника. В многоугольниках ребро является отрезком, лежащим на границе и чаще называется стороной многоугольника. В трёхмерных многогранниках и в многогранниках большей размерности ребро — это отрезок, общий для двух граней. Отрезок, соединяющий две вершины и проходящий через внутренние или внешние точки, ребром не является и называется диагональю.
Вложение Татта простого вершинно 3-связного планарного графа — вложение без пересечений с рёбрами в виде отрезков с дополнительными свойствами, что внешняя грань имеет выпуклый многоугольник в качестве границы и что каждая внутренняя вершина является геометрическим центром соседей. Если внешний многоугольник фиксирован, это условие на внутренние вершины определяет их положения однозначно как решение системы линейных уравнений. Решение уравнений даёт планарное вложение. Теорема Татта «о резиновой укладке» утверждает, что в единственном решении никогда нет пересечений рёбер и, что более строго, что любая грань получающегося планарного вложения выпукла. Вложение называется «резиновым», поскольку такое вложение может быть найдено как равновесное положение системы пружин или резиновых ремней, представляющих рёбра графа.

SPQR-дерево — это древесная структура данных, используемая в информатике, а именно, в алгоритмах на графах, для представления трёхсвязных компонент графа. Трёхсвязные компоненты двусвязного графа — это система более мелких графов, описывающих все 2-вершинные сечения графа. SPQR-дерево графа может быть построено за линейное время и имеет некоторые приложения в алгоритмах динамических графов и визуализации графов.

Фаска или усечение рёбер в геометрии — это топологическая операция, которая преобразует многогранник в другой многогранник. Операция подобна растяжению, передвигающему грани, удаляя их от центра. Для трёхмерных многогранников операция фаски добавляет новую шестиугольную грань вместо каждого исходного ребра.

Периферийный цикл в неориентированном графе — цикл, который, неформально говоря, не отделяет любую часть графа от любой другой. Периферийные циклы, первым изучал Татт, Уильям Томас. Они играют важную роль в описании планарных графов и в образовании циклических пространств непланарных графов.

Теорема Петерсена — одна из самых ранних теорем теории графов, названная в честь Юлиуса Петерсена. Определение теоремы может быть сформулировано следующим образом:
Теорема Петерсена. Любой кубический двусвязный граф содержит в себе совершенное паросочетание.













