
Гамма-функция — математическая функция. Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.

Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.

Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.

Фу́нкция Гри́на — функция, используемая для решения линейных неоднородных дифференциальных уравнений с граничными условиями . Названа в честь английского математика Джорджа Грина, который первым развил соответствующую теорию в 1830-е годы.
Пeрeда́точная фу́нкция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.
Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости. В теорию характеристических функций внесли большой вклад Ю. В. Линник, И. В. Островский, К. Р. Рао, Б. Рамачандран.
Производя́щая фу́нкция моме́нтов — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.
Преобразова́ние Лапла́са (ℒ) — интегральное преобразование, связывающее функцию  комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией  вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Ве́ктор Лапла́са — Ру́нге — Ле́нца — вектор, который используется для описания формы и ориентации орбиты, по которой одно небесное тело обращается вокруг другого. В случае с двумя телами, взаимодействие которых описывается законом всемирного тяготения Ньютона, вектор Лапласа — Рунге — Ленца представляет собой интеграл движения, то есть его направление и величина постоянны независимо от точки орбиты, в которой они вычисляются; говорят, что вектор Лапласа — Рунге — Ленца сохраняется при гравитационном взаимодействии двух тел. Это утверждение можно обобщить на любую задачу с двумя телами, взаимодействующими посредством центральной силы, которая изменяется обратно пропорционально квадрату расстояния между ними. Такая задача называется Кеплеровой задачей.
Теория линейных стационарных систем — раздел теории динамических систем, изучающий поведение и динамические свойства линейных стационарных систем (ЛСС). Используется для изучения процессов управления техническими системами, для цифровой обработки сигналов и в других областях науки и техники.
В математике и обработке сигналов преобразование Гильберта — линейный оператор, сопоставляющий каждой функции  функцию
функцию  в той же области.
в той же области.
Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований. Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач теории упругости, теплопроводности, электродинамики и других разделов математической физики. Использование интегральных преобразований позволяет свести дифференциальное, интегральное или интегро-дифференциальное уравнение к алгебраическому, а также, в случае дифференциального уравнения в частных производных, уменьшить размерность.
Дробное интегро-дифференцирование в математическом анализе — объединённый оператор дифференцирования/интегрирования, порядок которого может быть произвольным вещественным или комплексным числом. Используется в дробном математическом анализе. Сам по себе оператор служит для обозначения операции взятия производной/интеграла дробного порядка.
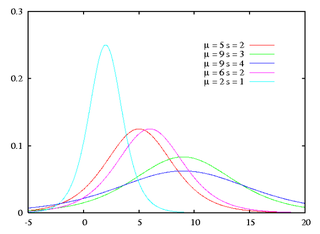
Логисти́ческое распределе́ние в теории вероятностей и математической статистике — один из видов абсолютно непрерывных распределений. Формой напоминает нормальное распределение, но имеет более «тяжёлые» концы и больший коэффициент эксцесса.
Преобразование Меллина — преобразование, которое можно рассматривать как мультипликативную версию двустороннего преобразования Лапласа. Это интегральное преобразование тесно связано с теорией рядов Дирихле и часто используется в теории чисел и в теории асимптотических разложений. Преобразование Меллина тесно связано с преобразованием Лапласа и преобразованием Фурье, а также теорией гамма-функций и теорией смежных специальных функций.
Преобразование Стилтьеса — это интегральное преобразование, которое для функции  имеет вид:
имеет вид:


В математике существует несколько интегралов, известных как интеграл Дирихле, названные в честь немецкого математика Петера Густава Лежена Дирихле, один из которых является несобственным интегралом функции sinc по положительной действительной прямой:

Метод функции Грина — метод решения линейного дифференциального уравнения, позволяет посредством нахождения соответствующей оператору этого уравнения функции Грина практически напрямую получить частное решение. Эффективность определяется возможностью записать функцию Грина в явном виде.
Теорема о свёртке гласит, что при подходящих условиях преобразование Фурье свёртки двух функций является поточечным произведением их преобразований Фурье. В более общем случае свёртка в одной области равна точечному умножению в другой области. Другие версии теоремы о свёртке применимы к различным преобразованиям Фурье.
































