Дельтообразный потенциал в квантовой механике

Дельтообра́зный потенциа́л в ква́нтовой меха́нике — общее название профилей потенциальной энергии частицы, задаваемых выражениями с дельта-функцией Дирака. Такими профилями моделируется физическая ситуация, когда наличествуют очень узкие и острые максимумы или минимумы потенциала.

Простыми примерами подобных профилей являются дельтообразный туннельный барьер и дельтообразная квантовая яма вида ${\displaystyle U(x)=\lambda /m\cdot \delta (x)}$, где ${\displaystyle \lambda }$ — некая константа (Дж${\displaystyle \cdot }$кг${\displaystyle \cdot }$м), положительная для барьера и отрицательная для ямы, ${\displaystyle x}$ — декартова координата, а ${\displaystyle m}$ — масса частицы. Ставится вопрос о коэффициенте прохождения частицы, а также о существовании и энергиях связанных состояний.

В большинстве случаев при рассмотрении поведения частицы ищется решение одномерного стационарного уравнения Шрёдингера с соответствующим потенциалом. Обычно предполагается, что частица перемещается только вдоль направления ${\displaystyle x}$, а движения в перпендикулярной плоскости ${\displaystyle yz}$ нет.

Стационарное одномерное уравнение Шрёдингера для волновой функции ${\displaystyle \psi (x)}$ имеет вид

${\displaystyle {\hat {H}}\psi (x)=\left[-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}+U(x)\right]\psi (x)=E\psi (x)}$,

где ${\displaystyle {\hat {H}}}$ — гамильтониан, ${\displaystyle \hbar }$ — постоянная Планка, ${\displaystyle E}$ — полная энергия частицы и ${\displaystyle U(x)=\lambda /m\cdot \delta (x)}$. После интегрирования этого уравнения по узкому участку вблизи нуля

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\int _{-\epsilon }^{+\epsilon }\psi ''(x)\,dx+\int _{-\epsilon }^{+\epsilon }U(x)\psi (x)\,dx=E\int _{-\epsilon }^{+\epsilon }\psi (x)\,dx,\quad \epsilon \rightarrow 0}$

получится

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left(\psi _{R}'(0)-\psi _{L}'(0)\ \right)+{\frac {\lambda }{m}}\psi (0)=0}$.

Крупные значки ${\displaystyle _{L}}$ и ${\displaystyle _{R}}$ обозначают области левее и правее барьера или ямы (от англ. left, right). В точке ${\displaystyle x=0}$ должны быть выполнены условие непрерывности волновой функции

${\displaystyle \psi _{L}(0)=\psi _{R}(0)}$

и условие непрерывности плотности потока вероятности

${\displaystyle {\frac {d\psi _{L}}{dx}}(0)={\frac {d\psi _{R}}{dx}}(0)-{\frac {2\lambda }{\hbar ^{2}}}\psi _{R}(0)}$.

Эти два условия актуальны вне зависимости от того, идёт ли речь о дельтообразном барьере или яме, а также (для ямы) от того, больше или меньше нуля величина энергии ${\displaystyle E}$ (для барьера вариант ${\displaystyle E<0}$ невозможен).

В этом разделе предполагается, что ${\displaystyle E>0}$, и рассматривается прохождение частицы через барьер или над ямой.

Барьер или яма делит пространство на две части (${\displaystyle x<0,\,\,x>0}$). В обеих этих областях решение уравнения Шрёдингера представляет собой плоские волны и может быть записано в виде их суперпозиции:

${\displaystyle \psi _{L}(x)=A_{r}e^{ikx}+A_{l}e^{-ikx},\quad x<0}$,

${\displaystyle \psi _{R}(x)=B_{r}e^{ikx}+B_{l}e^{-ikx},\quad x>0}$,

где ${\displaystyle k={\sqrt {2mE}}/\hbar }$ — волновой вектор. Маленькие индексы ${\displaystyle r}$ и ${\displaystyle l}$ при коэффициентах ${\displaystyle A}$ и ${\displaystyle B}$ указывают на направление волнового вектора вправо и влево. Связь между этими коэффициентами может быть найдена из условий для ${\displaystyle \psi }$ и ${\displaystyle \psi '}$ при ${\displaystyle x=0}$, выписанных в конце предыдущего раздела:

${\displaystyle A_{r}+A_{l}=B_{r}+B_{l}}$,

${\displaystyle ik(A_{r}-A_{l}-B_{r}+B_{l})=-{\dfrac {2\lambda }{\hbar ^{2}}}\left(B_{r}+B_{l}\right)}$.

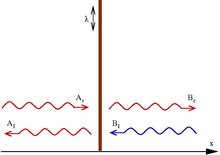
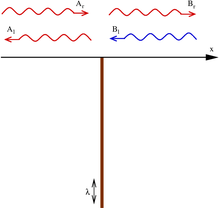
Пусть падающая частица приближается к барьеру слева (${\displaystyle A_{r}=1}$ и ${\displaystyle B_{l}=0}$), тогда коэффициенты ${\displaystyle A_{l}=r}$ и ${\displaystyle B_{r}=t}$, определяющие вероятность отражения и прохождения соответственно, имеют вид:

${\displaystyle t={\frac {1}{{\frac {i\lambda }{\hbar ^{2}k}}+1}},\qquad r={\frac {1}{{\frac {i\hbar ^{2}k}{\lambda }}-1}}}$.

В классическом случае частица с конечной энергией ${\displaystyle E>0}$ не может преодолеть бесконечный потенциальный барьер, а над ямой она проходит гарантированно. При квантовом же подходе ситуация иная: коэффициенты прохождения и отражения составляют

${\displaystyle T=|t|^{2}={\frac {1}{1+{\frac {\lambda ^{2}}{\hbar ^{4}k^{2}}}}}={\frac {1}{1+{\frac {\lambda ^{2}}{2m\hbar ^{2}E}}}}}$,

${\displaystyle R=|r|^{2}=1-T={\frac {1}{1+{\frac {\hbar ^{4}k^{2}}{\lambda ^{2}}}}}={\frac {1}{1+{\frac {2m\hbar ^{2}E}{\lambda ^{2}}}}}}$.

Здесь сразу три неожиданных, с классической точки зрения, результата. Во-первых, имеется ненулевая вероятность прохождения (коэффициент прохождения) для бесконечно высокого барьера. Во-вторых, поскольку формула вполне применима к отрицательным ${\displaystyle \lambda }$, вероятность надъямного прохождения отлична от единицы. В-третьих, значение ${\displaystyle T}$ не меняется при смене знака ${\displaystyle \lambda }$, то есть вероятности туннелирования частицы с энергией ${\displaystyle E}$ через барьер и надъямного прохождения той же частицы совпадают в числе.

В этом разделе предполагается, что ${\displaystyle E<0}$, и рассматривается только яма (${\displaystyle \lambda <0}$), а именно определяется энергия дискретного состояния частицы в ней.

В обеих областях решение уравнения Шрёдингера, как и выше, может быть записано в виде суммы экспонент

${\displaystyle \psi _{L}(x)=A_{r}e^{ikx}+A_{l}e^{-ikx},\quad x<0}$,

${\displaystyle \psi _{R}(x)=B_{r}e^{ikx}+B_{l}e^{-ikx},\quad x>0}$,

где ${\displaystyle k={\sqrt {2mE}}/\hbar }$. Но теперь ${\displaystyle k}$ является мнимой величиной, и поэтому в записи следует оставить только те экспоненты, которые затухают, а не возрастают, на плюс и минус бесконечности:

${\displaystyle \psi _{L}(x)=A_{l}e^{-ikx}=A_{l}e^{|k|x},\quad x<0}$,

${\displaystyle \psi _{R}(x)=B_{r}e^{ikx}=B_{r}e^{-|k|x},\quad x>0}$,

Из условий для ${\displaystyle \psi }$ и ${\displaystyle \psi '}$ при ${\displaystyle x=0}$ вытекает ${\displaystyle A_{l}=B_{r}}$ и, уже с учётом этого требования, ${\displaystyle |k|=-\lambda /\hbar ^{2}}$. Отсюда

${\displaystyle E_{level}=-{\frac {\lambda ^{2}}{2m\hbar ^{2}}}}$,

то есть в дельтообразной яме существует ровно один уровень с выписанной энергией.

Ситуация туннелирования через дельтообразный потенциал является предельным случаем туннелирования через прямоугольный барьер ширины ${\displaystyle a}$ и высоты ${\displaystyle V}$, в котором стремление ${\displaystyle a}$ к нулю, а ${\displaystyle V}$ к ${\displaystyle +\infty }$ происходит так, что произведение ${\displaystyle V\cdot a}$ постоянно и равно некоей константе ${\displaystyle g=\lambda /m}$.

Задача о туннелировании через дельтообразный барьер является стандартной модельной задачей квантовой механики. Она возникает, например, при описании токопереноса между двумя проводящими областями, на стыке которых самопроизвольно образуется тонкая окисная плёнка. Если толщина плёнки и её химический состав примерно известны, можно использовать модель прямоугольного или трапецеидального барьера. Однако в ряде случаев единственным выходом является привлечение модели дельтообразного потенциала.

Аналогично с задачей о дельтообразной яме: модель может использоваться в качестве грубого приближения. Значение ${\displaystyle \lambda }$ служит подгоночным параметром как для барьера, так и для ямы.

• Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5.