
Пло́щадь — в узком смысле, площадь фигуры — численная характеристика, вводимая для определённого класса плоских геометрических фигур и обладающая свойствами площади. Интуитивно, из этих свойств следует, что бо́льшая площадь фигуры соответствует её «большему размеру», a оценить площадь фигуры можно с помощью наложения на её рисунок сетки из линий, образующих одинаковые квадратики и подсчитав число квадратиков и их долей, попавших внутрь фигуры. В широком смысле понятие площади обобщается на k-мерные поверхности в n-мерном пространстве, в частности, на двумерную поверхность в трёхмерном пространстве.

Квадра́т — правильный четырёхугольник, то есть плоский четырёхугольник, у которого все углы и все стороны равны. Каждый угол квадрата — прямой  .
.

Прямоугольник — четырёхугольник, у которого все углы прямые.

Дельто́ид — четырёхугольник, у которого по две смежные стороны равны ; если бо́льшая пара смежных сторон изображена вверх, то очертания фигуры напоминают заглавную греческую букву Δ. В ранней литературе иногда также называется ромбоидом, однако в современной планиметрии ромбоидом обычно считается параллелограмм, не являющийся прямоугольником или ромбом.
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, целиком принадлежащей одной плоскости. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Гипотенуза — самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Теоре́ма Пифаго́ра — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Квадрату́ра кру́га — задача, заключающаяся в нахождении способа построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу. Наряду с трисекцией угла и удвоением куба, является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.

Кривая Леви — фрактал. Предложен французским математиком П. Леви. Получается, если взять половину квадрата вида /\, а затем каждую сторону заменить таким же фрагментом, и, повторяя эту операцию, в пределе получим кривую Леви.

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.
Пери́метр — общая длина границы фигуры. Имеет ту же размерность величин, что и длина.

Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.

Пифагореи́зм — название философского движения и направления древнегреческой философии, основателем которого был Пифагор Самосский. Оно возникло в VI—IV вв. до н. э. в Южной Италии, а затем распространилось на другие области. Последователей учения называют пифагорейцами. В узком смысле слова пифагорейцы — члены пифагорейского союза, созданного Пифагором в городе Кротон (Италия). В широком смысле слова — последователи учения Пифагора.

Теоре́ма де Гуа — одно из обобщений теоремы Пифагора на старшие размерности.
Исчезновение клетки — известный класс задач на перестановку фигур, обладающих признаками математических софизмов: изначально в их условие введена замаскированная ошибка. Некоторые из этих задач тесно связаны со свойствами последовательности чисел Фибоначчи.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.

Пропорционирование — способ гармонизации формы на основе равенства количественных отношений её частей. Пропорциональностью называют равенство (постоянство) отношений двух или более переменных величин. Иную редакцию той же закономерности даёт Большая российская энциклопедия: «Равенство между двумя отношениями четырёх величин». В математике пропорцией называется такое отношение (зависимость) величин, которое при увеличении или уменьшении одной величины в несколько раз другая увеличивается или уменьшается во столько же раз. Например, 1 : 2 = 3 : 6. Отношение таких величин называется коэффициентом пропорциональности или константой пропорциональности.

Треугольник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.

Треугольник Кеплера — это прямоугольный треугольник, длины сторон которого составляют геометрическую прогрессию. При этом соотношение длин сторон треугольника Кеплера связано с золотым сечением


Метод площадей — метод решения геометрических тождеств путём подсчёта площадей фигур разными способами.


 Классическое дерево Пифагора
Классическое дерево Пифагора Обдуваемое ветром дерево Пифагора
Обдуваемое ветром дерево Пифагора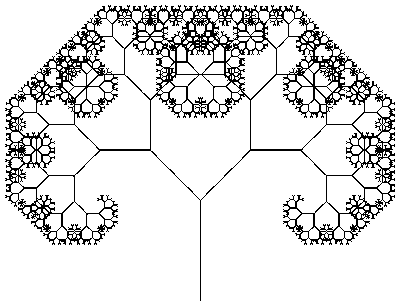 Обнаженное дерево Пифагора
Обнаженное дерево Пифагора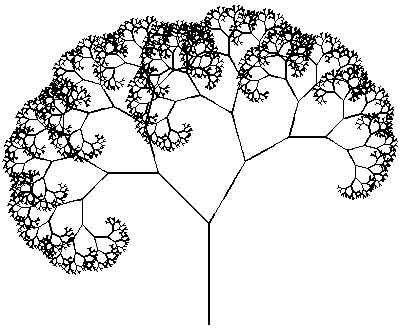 Обнаженное обдуваемое ветром дерево Пифагора
Обнаженное обдуваемое ветром дерево Пифагора

















