Диаграммы Солодовникова
Диаграммы (номограммы, кривые) Солодовникова — устанавливают связь между величиной перерегулирования σ%, временем переходного процесса tрег, максимальным значением вещественной части АФЧХ Pmax и частотой среза ωср.
Например, σ% = 25% и tрег = 2 с.
Значению σ% = 25% на графике σ(Pmax) соответствует значение tрег = на графике tрег(Pmax).
Отсюда можно найти ωп = = 5,34 рад/c.
Частота среза находится из условия: ωср = (0,6÷0,9)ωп.
По диаграммам для определения запасов устойчивости определяют запас устойчивости по фазе Δφ и амплитуде ΔL в зависимости от перерегулирования σ%.
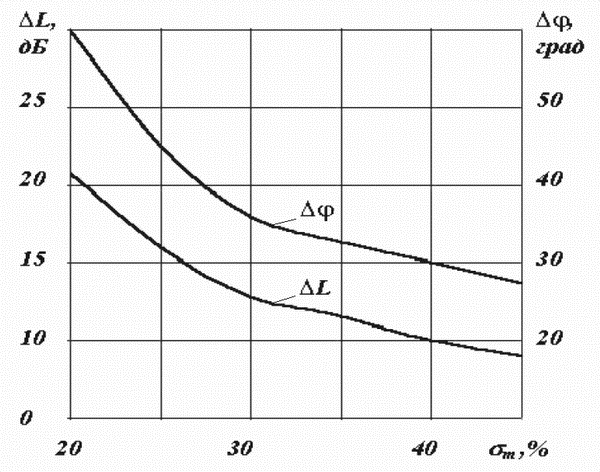
Зная запас устойчивости по амплитуде можно определить протяжённость среднечастотной асимптоты при синтезе САУ.
Например, для систем с астатизмом первого порядка запас устойчивости по амплитуде в отрицательной области ΔL2 будет по модулю равен запасу устойчивости ΔL1 в положительной области.
ΔL1 = |ΔL2|
Подобные диаграммы используются для синтеза желаемой ЛАЧХ системы.
К вопросу об автоматизации работы с номограммами
Поскольку вышеприведенные номограммы получены полуэмпирическим способом, то для упрощения работы с ними, имеет смысл получить их аппроксимированные зависимости. Такие зависимости получены и оформлены в виде функции системы MATLAB. Поскольку функция в системе MATLAB представлена в виде текстового файла, ниже приводится текст готовой функции:
function [omega_sr, Lm, gamma] = nomosol(sigma, t_pp)
% Номограмма Солодовникова, используемая для синтеза корректирующих звеньев
% методом построения желаемой ЛАЧХ.
%
% Вызов функции:% [omega_sr, Lm, gamma] = NOMOSOL(sigma);
% или
% [omega_sr, Lm, gamma] = NOMOSOL(sigma, t_pp);
%
% Входные данные:% sigma - желаемая величина перерегулирования, в процентах;
% t_pp - желаемое время переходного процесса, в секундах.
%
% Выходные данные:% omega_sr - минимальная частота среза, рад/сек.
%
% Lm - предельное значение логарифмической амплитуды, dB
%
% gamma - избыток фазы, градусы
%
% ПРИМЕЧАНИЕ:% Если обращение к функции выполнено согласно первому способу,
% когда t_pp не вводится, выходная переменная omega_sr является
% функцией от t_pp: omega_sr = f(t_pp) = @(t_pp) c*pi/t_pp
% где t_pp - время переходного процесса, сек
% с - константа, определяемая по номограмме.
% Во втором случае частота среза omega_sr принимает численное значение.
%
% Одновременно в функцию вводится только одно значение или одна пара
% значений входных элементов
%
% Данная функция основана на номограмме Солодовникова, опубликованной
% в книге:%
% Теория автоматического управления: Учеб. для вузов по спец. «Автоматика и
% телемеханика». В 2-х ч. Ч. 1. Теория линейных систем автоматического
% управления / Н.А. Бабаков, А.А. Воронов, А.А. Воронова и др.; Под ред.
% А.А.Воронова. - 2-е изд., перераб. и доп. - М.: Высш. шк., 1986. - 367с., ил.
%
% В приведенной книге номограммы опубликованы на страницах 272 и 273.
%
% Автор функции: асс. кафедры Гидрогазодинамика, СНУ им. В. Даля.
% Мушкаев Ярослав Владимирович, E-Mail:ysms@ukr.net
% 20-ноя-2011
switch nargin
case 1
fun_out = true;
case 2
fun_out = false;
otherwise
disp('Неверный ввод!');
omega_sr = NaN; Lm = NaN; gamma = NaN;
return
end
if length(sigma(:)) ~= 1
disp('Переменная sigma не может быть вектором или матрицей!');
omega_sr = NaN; Lm = NaN; gamma = NaN;
return
end
if ~and(sigma >= 17.55, sigma <= 38.3)
disp('Значения искомых параметров не могут быть определены');
disp('для заданного sigma: 17.55% <= sigma <= 38.3%');
omega_sr = NaN; Lm = NaN; gamma = NaN;
return
end
C_sigma = [ 508.321058427288, -3060.22544945687, 7415.40549715130, -8983.52110625671, 5457.12316398637, -1319.55483588478;];
C_tpp = [ 55.6639314226042, -311.896064410782, 680.562835356507, -709.420175449177, 347.438353856472, -60.0893038609672;];
C_Lm = [ 3395.09767299379, -28707.9450565944, 100993.514061531, -189260.381855314, 199355.799306957, -112003.345584484, 26268.4759050036;];
C_gamma_grad = [ -62.2007064137489, 1785.51295903594, -10389.4884037248, 26305.9467171758, -33647.4713334065, 21241.5288609184, -5161.27087502216;];
P_max = roots([C_sigma(1:end-1), C_sigma(end)-sigma]);
P_max(or(logical(imag(P_max)), P_max < 0)) = [];
c = polyval(C_tpp, P_max);
omega_sr = eval(['@(t_pp) ' num2str(c, '%.2f') '*pi/t_pp']);
if ~fun_out
omega_sr = omega_sr(t_pp);
end
Lm = polyval(C_Lm, P_max);
gamma = polyval(C_gamma_grad, P_max);
Для того, чтобы можно было этой функцией воспользоваться, нужно скопировать текст программы со страницы и сохранить его под именем nomosol.m в одной из папок, видимой для системы MATLAB. Имя файла может быть и другим, но, согласно синтаксиса MATLAB, должно совпадать с именем первой функции внутри файла.
Следует заметить, что эту функцию вполне можно использовать в математических пакетах, имеющих схожий с MATLAB синтаксис или после небольшой переделки.
Работа функции гарантирована для версий Матлаб не ниже 7.x. Для других версий, возможно, потребуется незначительная переработка.