Диаметр
Диа́метр (фр. diamètre из лат. diametrus из др.-греч. διάμετρος — поперечник[1]) — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Обобщённо диаметром фигуры (множества) называется максимальное расстояние между точками этой фигуры (множества), или точная верхняя грань всевозможных расстояний, если максимальное не существует.
Диаметр геометрических фигур
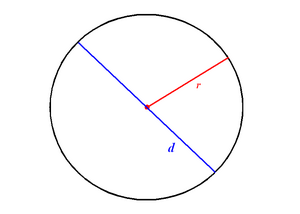
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.
Символ диаметра
| Диаметр | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ⌀ | ||||||||||||
Изображение
| ||||||||||||
| ||||||||||||
| Характеристики | ||||||||||||
| Название | diameter sign | |||||||||||
| Юникод | U+2300 | |||||||||||
| HTML-код | ⌀ или ⌀ | |||||||||||
| UTF-16 | 0x2300 | |||||||||||
| URL-код | %E2%8C%80 | |||||||||||
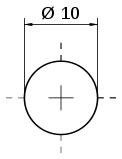
В инженерной графике и технических спецификациях диаметр принято обозначать символом ![]() [2]. Символ диаметра представлен в Юникоде (U+2300 ⌀ diameter sign)[3] и, хотя он отсутствует в стандартных раскладках клавиатуры, может быть введён с клавиатуры:
[2]. Символ диаметра представлен в Юникоде (U+2300 ⌀ diameter sign)[3] и, хотя он отсутствует в стандартных раскладках клавиатуры, может быть введён с клавиатуры:
- в HTML как
⌀или⌀ - в LaTeX для его отображения предназначена команда
\diameterиз пакета wasysym - в Microsoft Word символ можно получить, введя 2300 и нажав Alt+X
- в Windows с помощью Alt-кода Alt+8960 (в английской раскладке)
- в системах, использующих X Window System (Unix/Linux/ChromeOS и др.), с помощью комбинации Ctrl+⇧ Shift+u 2300Пробел или с использованием клавиши Compose, нажав поочерёдно Composedi[4].
Также, символ можно найти и скопировать в приложениях и инструментах типа «таблица символов», например:
- в Windows — Таблица символов[англ.]
- в программах из пакета Microsoft Office — меню «Вставка» → «Символ…»
- в macOS — Character Palette/Viewer (вызывается комбинацией ⌥ Opt+⌘ Cmd+T)
- в GNOME — Таблица символов GNOME (ранее — gucharmap).
Во многих случаях символ диаметра может не отображаться, так как его редко включают в шрифты (он присутствует, например, в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других), в связи с чем вместо него часто используются другие символы со схожим начертанием. К примеру, в САПР AutoCAD вместо символа диаметра используется символ пустого множества (U+2205 ∅ empty set), вводящийся сочетанием %%c (буква c — латинская) или \U+2205 в текстовой строке. Взаимозаменяемость этих символов отражена и в стандартах консорциума W3C[5]. Также, для замены часто используется буква Ø датско-норвежского алфавита.
Сопряжённые диаметры эллипса и гиперболы
Сопряжённые диаметры эллипса

- Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
На рисунке представлена пара сопряжённых диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зелёные линии на рисунке).
- Расстояния и от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле , где — угол между радиус-вектором данной точки и осью абсцисс.
Сопряжённые диаметры гиперболы
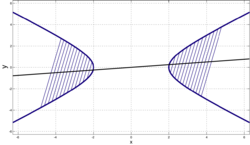
- Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
- Угловой коэффициент параллельных хорд и угловой коэффициент соответствующего диаметра связан соотношением
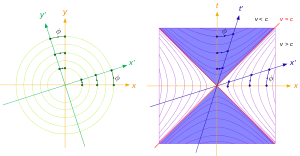
Для произвольного угла φ показаны диаметры и сопряжённые им диаметры для окружностей и равнобочных гипербол.
- Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
- Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
- В случае гипербол с асимптотами, образующими прямой угол, её сопряжённые гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряжённый диаметр, который будет просто диаметром сопряжённой гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряжённых диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряжённых диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).
Диаметр кубики
Диаметр кубики — прямая, на которой лежат середины хорд кубики, параллельных одной из её асимптот[6].
Кубика может иметь один диаметр, три диаметра или не иметь ни одного[7]. В последнем случае середины хорд кубики, параллельных одной из её асимптот, лежат на гиперболе[8].
- Кубики с диаметрами и без
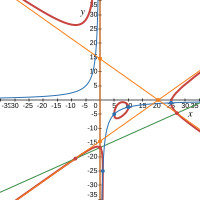 Кубика без диаметров
Кубика без диаметров Кубика c одним диаметром
Кубика c одним диаметром Кубика c тремя диаметрами
Кубика c тремя диаметрами
Вариации и обобщения
Понятие диаметра допускает естественные обобщения на некоторые другие геометрические и математические объекты. Если во множестве некоторых объектов определена метрика пространства, то для подмножества этих объектов может быть введено понятие диаметра множества.
Диаметром множества , лежащего в метрическом пространстве с метрикой , называется величина .
Под диаметром метрического пространства понимается точная верхняя грань расстояний между парой любых его точек.
- В частности:
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние измеренное в количестве рёбер между двумя вершинами графа, максимально удалёнными друг от друга.
- Максимальное расстояние Хэмминга между двумя словами равной в символах длины равно , другими словами диаметр множества слов в метрике Хэмминга равен .
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
Например, диаметр n-размерного гиперкуба со стороной s равен
- .
Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре
- Окружность Фурмана построена на одном отрезке, как на диаметре
- Окружность Брокара построена на одном отрезке, как на диаметре
См. также
- Радиус
- Пи
- При делении фигур на части меньшего диаметра возникла гипотеза Борсука, опровергнутая в 1993 году
- Изодиаметрическое неравенство
- Угловой диаметр астрономических объектов.
- Диаметр циркуляции
- Гидравлический диаметр
Примечания
- ↑ диаметр // Этимологический словарь русского языка = Russisches etymologisches Wörterbuch : в 4 т. / авт.-сост. М. Фасмер ; пер. с нем. и доп. чл.‑кор. АН СССР О. Н. Трубачёва, под ред. и с предисл. проф. Б. А. Ларина [т. I]. — Изд. 2-е, стер. — М. : Прогресс, 1986—1987.
- ↑ Большаков В. П., Тозик В. Т., Чагина А. В. Инженерная и компьютерная графика. — СПб.: БХВ-Петербург, 2013. — 288 с. — ISBN 978-5-9775-0422-5. — С. 90.
- ↑ The Unicode Standard, Version 13.0. Miscellaneous Technical, Range: 2300–23FF (англ.) (PDF). Unicode Inc[англ.] (2020). Дата обращения: 6 сентября 2020. Архивировано 30 декабря 2019 года.
- ↑ Monniaux, David UTF-8 (Unicode) compose sequence (англ.). — Файл конфигурации вводимых с помощью клавиши Compose символов. Дата обращения: 6 сентября 2020. Архивировано 3 августа 2020 года.
- ↑ SYMBOL Characters and Glyphs. Дата обращения: 6 сентября 2020. Архивировано 6 августа 2020 года.
- ↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 16.
- ↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 7.
- ↑ Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка, 1961, § 1. Классификация Ньютона, с. 10.
Литература
- Диаметр // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Смогоржевский А. С., Столова Е. С. Справочник по теории плоских кривых 3-го порядка. М.: Физматлит, 1961. 271 с., ил.