Дифракционная решётка

Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность.
История
Первое описание явления сделал в 1673 году Джеймс Грегори, который наблюдал дифракцию на птичьих перьях:
Если вы сочтёте нужным, вы можете показать мистеру Ньютону небольшой эксперимент, который (если он еще не знает об этом) будет достоин его внимания. Впустите солнечный свет через маленькое отверстие в затемнённый дом, а в отверстие поместите перо (чем тоньше и белее, тем лучше для этой цели), и оно направит на белую стену или бумагу напротив нее ряд маленьких кругов и овалов (если я их не ошибаюсь), из которых один белый (а именно середина, которая противоположна Солнцу), а все остальные по-разному окрашены. Я с радостью выслушаю его мысли об этом.[1]
Дэвид Риттенхаус в 1786 году впервые изготовил дифракционную решётку и измерил углы отклонения для разных цветов[2].
В 1801 году Томас Юнг открыл и объяснил интерференцию света. В 1818 году Огюстен Жан Френель разработал теорию дифракции света.
Опираясь на представления Юнга и Френеля о световых волнах, Йозеф Фраунгофер в 1821 году впервые использовал дифракционную решётку (которую он и изготовил) для получения спектров и вычисления длин волн.
Виды решёток
- Отражательные — Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отражённом свете
- Прозрачные — Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете.
Описание явления

Идеализированная решетка состоит из набора щелей с периодом d, который должен быть больше, чем длина волны, представляющая интерес, чтобы вызвать дифракцию. Пусть на решетку нормально (перпендикулярно решетке) падает плоская волна монохроматического света с длиной волны , тогда каждая щель в решетке действует как квазиточечный источник, из которого свет распространяется во всех направлениях согласно с принципом Гюйгенса — Френеля. Происходит интерференция света, излученного всеми щелями, при этом если в каком-то направлении свет от двух соседних щелей оказывается в одинаковой фазе, происходит конструктивная интерференция, и в этом направлении появляется максимум. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр.
Формулы

Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.
Если известно число штрихов (), приходящихся на 1 мм решётки, то период решётки находят по формуле: мм.
При нормальном падении плоской волны условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
где
- — период решётки,
- — угол максимума данного цвета,
- — порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,
- — длина волны.
Это условие может быть выведено исходя из того, что разность фаз между лучами, отраженными от поверхностей на расстоянии, равном периоду решетки, должна быть кратна , или, другими словами, разность оптических путей кратна длине волны. При этом положение максимумов зависит только от периода решетки, а ширина щели или форма штрихов влияет на плавную огибающую функции максимумов.
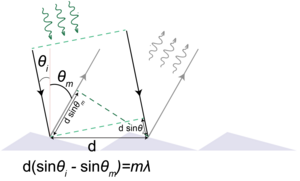
Если же свет падает на решётку под углом , то:
Эта формула может быть проиллюстрирована графически, для того, чтобы найти направление на какой-то порядок дифракции, необходимо нарисовать окружность с радиусом, равным периоду решетки, умноженному на показатель преломления вещества, в котором наблюдаются порядки. Затем через конец прошедшего или отражённого луча необходимо провести вертикальную прямую. После этого, необходимо провести еще несколько вертикальных прямых на расстоянии друг от друга, равным длине волны. Направления на порядки дифракции будут из центра окружности в точки, где она пересекается с вертикальными прямыми. Фактически, такая иллюстрация аналогична построению Эвальда в одномерном случае.
Характеристики
Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом для длины волны λ и под углом +Δ — для длины волны λ+Δλ. Угловой дисперсией решётки называется отношение D=Δ/Δλ. Выражение для D можно получить, если продифференцировать формулу дифракционной решётки
Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра m.
Вторая характеристика дифракционной решетки — разрешающая способность. Она обусловлена угловой шириной главного максимума и определяет возможность раздельного наблюдения 2 близких спектральных линий. При увеличении порядка спектра m возрастает
Также существует еще одна характеристика дифракционной решетки — дисперсионная область. Она определяет для каждого порядка спектральный диапазон от перекрытия спектров. Данный параметр обратно-пропорционален порядку спектра m
Изготовление
Хорошие решётки требуют очень высокой точности изготовления. Если хоть одна щель из множества будет нанесена с ошибкой, то решётка будет бракована. Машина для изготовления решёток прочно и глубоко встраивается в специальный фундамент. Перед началом непосредственного изготовления решёток, машина работает 5—20 часов на холостом ходу для стабилизации всех своих узлов. Нарезание решётки длится до 7 суток, хотя время нанесения штриха составляет 2—3 секунды.
Применение
Дифракционную решётку применяют в спектральных приборах, также в качестве оптических датчиков линейных и угловых перемещений (измерительные дифракционные решётки).

Примеры

Один из простейших и распространённых в быту примеров отражательных дифракционных решёток — компакт-диск. На поверхности компакт-диска — дорожка в виде спирали с шагом 1,6 мкм между витками. Примерно треть ширины (0,5 мкм) этой дорожки занята углублением (это записанные данные), рассеивающим падающий на него свет, примерно две трети (1,1 мкм) — нетронутая подложка, отражающая свет. Таким образом, компакт-диск — отражательная дифракционная решётка с периодом 1,6 мкм. Кроме того, такой же отражательной дифракционной решёткой является и пустой CD-R диск, и пустой DVD диск, поскольку на них имеется спиральная дорожка для направления луча лазера при записи информации. Причём период решётки для DVD — 0,74 мкм.
См. также
- Дифракция на N щелях
- Дифракция Фраунгофера
- Дифракция Френеля
- Интерференция света
- Фурье-оптика
- Оптическая решётка
- Призма (оптика)
Примечания
- ↑ Letter from James Gregory to John Collins, dated 13 May 1673. Reprinted in: Correspondence of Scientific Men of the Seventeenth Century…., ed. Stephen Jordan Rigaud (Oxford, England: Oxford University Press, 1841), vol. 2, page 254. Books.Google.com Архивная копия от 16 сентября 2020 на Wayback Machine.
- ↑ И. Д. Багбая. К истории дифракционной решётки. Успехи физических наук, т. 108, вып. 2, октябрь 1972. стр. 335-337.. Дата обращения: 21 августа 2020. Архивировано 12 августа 2017 года.
Литература
- Эшелетты // Элоквенция — Яя. — М. : Советская энциклопедия, 1957. — С. 293. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 49).
- Ландсберг Г. С. Оптика, 1976
- Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- Тарасов К. И. Спектральные приборы, 1968
Ссылки
- Экспериментальное определение периода решётки у компакт-диска — видео с пояснениями на английском языке



























