А́лгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики; в этом разделе числа и другие математические объекты обозначаются буквами и другими символами, что позволяет записывать и исследовать их свойства в самом общем виде. Слово «алгебра» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под «алгеброй» понимают раздел математики, посвящённый изучению операций над элементами множеств произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Общая алгебра — раздел математики, изучающий алгебраические системы, такие как группы, кольца, поля, модули, решётки, а также отображения между такими структурами.
Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством разнообразных вычислений. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач. Современная вычислительная математика включает в круг своих проблем изучение особенностей вычисления с применением компьютеров.
Произво́дная — производящая, образующая другую более сложную составную величину категории.
Произво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой.
Дифференциальными кольцами, полями и алгебрами называются кольца, поля и алгебры, снабжённые дифференцированием — унарной операцией, удовлетворяющей правилу произведения. Естественный пример дифференциального поля — поле рациональных функций одной комплексной переменной 
, операции дифференцирования соответствует дифференцирование по 
. Теория создана Джозефом Риттом (1950) и его учеником Эллисом Колчином.
Производная — фундаментальное математическое понятие, используемое в различных вариациях (обобщениях) во многих разделах математики. Это базовая конструкция дифференциального исчисления, допускающая много вариантов обобщений, применяемых в математическом анализе, дифференциальной топологии и геометрии, алгебре.
Опера́тор — математическое отображение между множествами, в котором каждое из них наделено какой-либо дополнительной структурой. Понятие оператора используется в различных разделах математики для отличия от другого рода отображений ; точное значение зависит от контекста, например в функциональном анализе под операторами понимают отображения, ставящие в соответствие функции другую функцию.
А́лгебра Ли — объект общей алгебры, являющийся векторным пространством с определенной на ней антикоммутативной билинейной операцией, удовлетворяющей тождеству Якоби. В общем случае алгебра Ли является неассоциативной алгеброй. Названа по имени норвежского математика Софуса Ли (1842—1899).
Антикоммутативность — свойство мультипликативной бинарной операции в кольце: 
.
Обобщённая фу́нкция, или распределе́ние, — математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах.
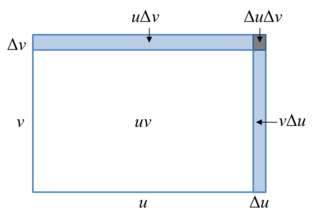
Правило произведения, или тождество Лейбница, — характерное свойство дифференциальных операторов.
Тангенциальнозначные формы — это обобщение дифференциальных форм, при котором множеством значений формы является касательное расслоение к многообразию.
Опера́ция — отображение, ставящее в соответствие одному или нескольким элементам множества (аргументам) другой элемент (значение). Термин «операция» как правило применяется к арифметическим или логическим действиям, в отличие от термина «оператор», который чаще применяется к некоторым отображениям множества на себя, имеющим интересные для исследований свойства.
Дифференцирование в алгебре — операция, обобщающая свойства различных классических производных и позволяющая ввести дифференциально-геометрические идеи в алгебраическую геометрию. Изначально это понятие было введено для исследования интегрируемости выражений в элементарных функциях алгебраическими методами.
Система компьютерной алгебры — это прикладная программа для символьных вычислений, то есть выполнения преобразований и работы с математическими выражениями в аналитической (символьной) форме.
Ве́кторное исчисле́ние — раздел математики, в котором изучаются свойства операций над векторами.
Формальное дифференцирование — операция над элементами кольца многочленов или кольца формальных степенных рядов, повторяющая взятие производной из математического анализа, но не опирающееся на понятие предела, которое невозможно определить для произвольного кольца. Многие свойства производной верны и для формального дифференцирования, но некоторые, особенно касающиеся утверждений, содержащих числа, не верны. Одно из важных применений формального дифференцирование в алгебре — проверка кратности корней полиномов.
