Задача о 100 узниках и 100 ящиках

Задача о 100 узниках и 100 ящиках — задача в теории вероятностей и комбинаторике. Суть задачи заключается в том, что каждый из 100 узников должен найти свой номер в одном из 100 ящиков, чтобы все они выжили; если хотя бы один не справится, умрут все. Каждый узник может открыть только 50 ящиков и не может общаться с другими узниками, за исключением предварительного обсуждения стратегии.

На первый взгляд ситуация выглядит безнадёжной, но существует стратегия, которая даёт узникам шанс на выживание примерно в 30 %. Задача была предложена датским учёным в области информатики Питером Мильтерсеном в 2003 году.

В литературе встречаются разные условия задачи. Ниже приведена версия Филиппа Флажоле и Роберта Седжвика^[1].

Начальник тюрьмы предлагает ста узникам, приговорённым к смертной казни, последний шанс. Узники пронумерованы от 1 до 100, а комната содержит шкаф со 100 ящиками. Начальник случайным образом помещает в каждый ящик по одному из номеров от 1 до 100, во все ящики — разные номера. Узники по очереди входят в комнату. Каждый узник может открыть и проверить 50 ящиков в любом порядке. После каждого узника ящики снова закрываются, а все номера остаются в ящиках. Если каждый из узников найдёт в одном из ящиков свой номер, то все узники будут помилованы; если хотя бы один узник не найдёт свой номер, все узники будут казнены. Прежде чем первый узник войдёт в комнату, узники могут обсудить стратегию, но не могут общаться после этого момента. Какова лучшая для узников стратегия?

Подразумевается, что номера узников распределены по ящикам случайно и потому все перестановки номеров узников по ящикам равновероятны. Также подразумевается, что ящики пронумерованы также от 1 до 100, либо об однозначности такой нумерации возможно договориться заранее.

Если узник выбирает 50 ящиков из 100 случайным образом, вероятность того, что он найдет свой номер, составляет 50 %. Вероятность того, что все узники, открывая случайные ящики, найдут свои номера, является произведением вероятностей успеха отдельных узников, то есть

${\displaystyle \left({\frac {1}{2}}\right)^{100}}$ ≈ 0,0000000000000000000000000000008

— исчезающе малое число. Ситуация кажется безнадёжной.

Существует стратегия, которая обеспечивает вероятность более, чем в 30 %, что узники выживут. Ключ к успеху заключается в том, что узникам не нужно заранее решать, какие ящики открывать: каждый может использовать информацию, полученную из содержимого уже открытых им ящиков, чтобы решить, какой из них открыть следующим. Другое важное наблюдение заключается в том, что успешность одного узника не является независимой от успешности других, поскольку все они зависят от раскладки номеров по ящикам^[2].

Для описания стратегии предположим, что не только узники, но и ящики пронумерованы от 1 до 100 — например, строка за строкой, начиная с верхнего левого ящика. Стратегия такова^[3]:

1. Каждый узник сначала открывает ящик со своим номером.
2. Если этот ящик содержит его номер, узник добился успеха.
3. В противном случае ящик содержит номер другого узника, и он открывает ящик с этим номером.
4. Узник повторяет шаги 2 и 3, пока не найдет свой номер или не откроет 50 ящиков.

Начиная перебор со своего собственного номера и идя по циклу, узник гарантирует, что находится в последовательности ящиков, заканчивающейся на его номер. Успешность его действий зависит только от того, будет ли эта последовательность длиннее 50 ящиков.

В модифицированном варианте задачи, где добавлен ещё один персонаж — адвокат, которому разрешено открыть все ящики и, при необходимости, поменять местами содержимое двух из них, выживание узников становится независимым от изначальной перестановки: для этого адвокат, обнаружив цикл длиннее 50 ящиков, разбивает его на два цикла длины не более 50.

Причина успешности этой стратегии может быть проиллюстрирована на следующем примере — в нём 8 узников и ящиков, каждый узник может открыть 4 ящика. Предположим, что начальник тюрьмы распределил номера узников по ящикам следующим образом:

номера ящиков	1	2	3	4	5	6	7	8
номера узников	7	4	6	8	1	3	5	2

Согласно приведённой выше стратегии, узники действуют следующим образом:

• Узник 1 сначала открывает ящик 1 и находит номер 7. Затем он открывает ящик 7 и находит номер 5. Затем он открывает ящик 5, где находит свой номер и тем самым добивается успеха.
• Узник 2 открывает по порядку ящики 2, 4 и 8. В последнем ящике он находит свой номер.
• Узник 3 открывает ящики 3 и 6; в последнем он находит свой номер.
• Узник 4 открывает ящики 4, 8 и 2, прежде чем находит свой номер. Обратите внимание, что это тот же цикл, с которым столкнулся узник 2, хотя ни один из этих узников не знает об этом.
• Узники с 5 по 8 также найдут свои номера похожим способом.

В данном примере все узники находят свои номера, однако это не всегда так. Например, если поменять содержимое ящиков 5 и 8, то узник 1 использует все свои попытки, открыв ящики 1, 7, 5 и 2, и не найдет свой номер:

номера ящиков	1	2	3	4	5	6	7	8
номера узников	7	4	6	8	2	3	5	1

А при следующей расстановке узник 1 откроет ящики 1, 3, 7 и 4 и также не добьётся успеха:

номера ящиков	1	2	3	4	5	6	7	8
номера узников	3	1	7	5	8	6	4	2

В действительности в этом примере все узники, кроме 6, не смогут найти ящик со своим номером.

Раскладку номеров узников по ящикам можно описать математически как перестановку чисел от 1 до 100. Такая перестановка представляет собой взаимно-однозначное отображение множества натуральных чисел от 1 до 100 на себя. Последовательность чисел, такая что первое переходит во второе, второе — в третьем, и так далее, а последнее — в первое, называется циклом перестановки. Каждая перестановка может быть разложена на непересекающиеся циклы, то есть циклы, которые не имеют общих элементов. Перестановка из первого примера выше может быть записана в циклической записи как

${\displaystyle (1~7~5)(2~4~8)(3~6)}$

и, таким образом, состоит из двух циклов длины 3 и одного цикла длины 2. Перестановка из второго примера — это, соответственно,

${\displaystyle (1~3~7~4~5~8~2)(6)}$

и состоит она из одного цикла длины 7 и одного цикла длины 1.

Циклическая запись не единственна, поскольку цикл длины ${\displaystyle l}$ может быть записан ${\displaystyle l}$ разными способами в зависимости от выбора первого числа. Открывая ящики по предложенной выше стратегии, каждый узник следует по циклу, который завершается его собственным номером. В случае восьми узников эта стратегия приводит к успеху тогда и только тогда, когда длина самого длинного цикла перестановки составляет не более 4. Если перестановка содержит цикл длиной 5 или более, все узники, чьи номера лежат в таком цикле, не достигают своего номера после четырех шагов.

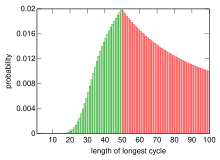
В первоначальной задаче 100 узников добьются успеха, если самый длинный цикл перестановки имеет длину не более 50. Следовательно, вероятность их выживания равна вероятности того, что случайная перестановка чисел от 1 до 100 не содержит цикла длиной более 50. Эта вероятность определяется следующим образом.

Перестановка чисел от 1 до 100 может содержать не более одного цикла длины ${\displaystyle l>50}$. Существует ${\displaystyle {\tbinom {100}{l}}}$ способов выбора чисел для такого цикла, где скобки обозначают сочетания. Эти числа могут быть расположены по циклу ${\displaystyle (l-1)!}$ способами, так как из-за циклической симметрии есть ${\displaystyle l}$ способов записать один и тот же цикл длины ${\displaystyle l}$. Остальные числа можно расположить ${\displaystyle (100-l)!}$ способами. Итого, число перестановок чисел от 1 до 100 с циклом длины ${\displaystyle l>50}$ равно

${\displaystyle {\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}}$.

Вероятность того, что (равномерно распределённая) случайная перестановка не содержит цикла длиной более 50, рассчитывается как

${\displaystyle 1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183}$,

где ${\displaystyle H_{n}}$ — ${\displaystyle n}$-ое гармоническое число. Поэтому, используя стратегию следования по циклу, узники выживают примерно в 31 % случаев^[3]. Удивительно, но это больше, чем 25 % — вероятность успеха всего двух узников, выбирающих ящики случайно и независимо.

Если вместо 100 узников рассмотреть ${\displaystyle 2n}$ узников, где ${\displaystyle n}$ — произвольное натуральное число, вероятность выживания узников при использовании стратегии следования по циклу определяется как

${\displaystyle 1-(H_{2n}-H_{n})=1-(H_{2n}-\ln 2n)+(H_{n}-\ln n)-\ln 2}$.

Пусть ${\displaystyle \gamma }$ — постоянная Эйлера — Маскерони. Тогда при ${\displaystyle n\to \infty }$ получаем

${\displaystyle \lim _{n\to \infty }(H_{n}-\ln n)=\gamma }$,

а потому вероятность выживания стремится к

${\displaystyle \lim _{n\to \infty }(1-H_{2n}+H_{n})=1-\gamma +\gamma -\ln 2=1-\ln 2\approx 0.30685}$.

Поскольку последовательность вероятностей монотонно уменьшается, при использовании стратегии следования по циклу узники выживают более чем в 30 % случаев независимо от количества узников^[3].

В 2006 году Юджин Кертин и Макс Варшавер доказали оптимальность стратегии следования по циклу. Доказательство основано на эквивалентности с похожей задачей, в которой всем узникам разрешено присутствовать в комнате и наблюдать за открытием ящиков. Математически эта эквивалентность основана на лемме Фоаты о переходе^[англ.] — взаимно-однозначном соответствии между (каноническими) циклическими обозначениями и стандартной записью перестановки^[]. В новой задаче вероятность выживания не зависит от выбранной стратегии и равна вероятности выживания в исходной задаче при использовании стратегии следования по циклу. Поскольку произвольная стратегия для исходной задачи также может быть применена к новой задаче, но она не может достичь более высокой вероятности выживания, стратегия следования по циклу должна быть оптимальной^[2].

Задача о 100 узниках и 100 ящиках была впервые рассмотрена в 2003 году датским ученым в области информатики Питером Мильтерсеном, который опубликовал её вместе с Анной Галь в отчёте о результатах 30-го международного коллоквиума по автоматам, языкам и программированию (ICALP^[англ.]). В их версии игрок A (начальник тюрьмы) случайным образом раскрашивает полоски бумаги с именами игроков команды B (узников) в красный или синий цвет и помещает каждую полоску в отдельный ящик, при том что некоторые из ящиков могут быть пустыми. Чтобы команда B выиграла, каждый из её членов должен правильно назвать свой цвет после того, как он открыл половину ящиков^[4].

Первоначально Милтерсон предполагал, что вероятность выигрыша быстро стремится к нулю с увеличением количества игроков. Однако Свен Скайум, коллега Мильтерсена из Орхусского университета, придумал стратегию следования по циклу для разновидности задачи, в которой нет пустых ящиков. В итоге в статье нахождение этой стратегии было оставлено как упражнение. Статья была удостоена^[] награды за лучшую публикацию^[2].

Весной 2004 года эта задача появилась в колонке головоломок от Джо Бюлера и Элвина Берлекэмпа в ежеквартальном издании The Emissary Научно-исследовательского института математических наук^{[англ.][5]}. В последующие годы эта задача стала использоваться в математической литературе в различных формулировках — например, с карточками на столе^[6] или кошельками в шкафчиках^[2].

В форме задачи о 100 узниках и 100 ящиках она была поставлена в 2006 году Кристофом Пеппе в журнале Spektrum der Wissenschaft (немецкой версии Scientific American)^[7] и Питером Уинклером в College Mathematics Journal^{[англ.][8]}. С небольшими изменениями этот вариант был использован в учебниках комбинаторики Филиппа Флажоле^[англ.] и Роберта Седжвика^[1], а также Ричардом Стэнли^{[англ.][3]}.

• Задача трёх узников

• Philippe Flajolet^[англ.], Robert Sedgewick. Analytic Combinatorics (англ.). — Cambr.: Cambridge University Press, 2009. — 824 p. — ISBN 978-0-521-89806-5.
• Richard P. Stanley^[англ.]. Algebraic Combinatorics: Walks, Trees, Tableaux, and More (англ.). — Springer, 2013. — 223 p. — ISBN 978-1-46146-998-8.
• Peter Winkler. Mathematical Mind-Benders (англ.). — Taylor & Francis, 2007. — 160 p. — ISBN 978-1-56881-336-3.