GNOME terminal — это эмулятор терминала, написанный Хэвоком Пеннингтоном и другими. Это часть свободного набора программ GNOME. Терминал позволяет пользователям GNOME выполнять команды, используя настоящий UNIX shell из графической оболочки. Это позволяет передвигать окно терминала, изменять его размеры и перемещать на другой рабочий стол так же, как и любое окно GNOME.

Замощение, тесселяция — автоматизированный процесс добавления новых выпуклых многоугольников в полигональную сетку с целью повышения детализации сетки.

Мозаика Пенроуза — общее название трёх особых типов непериодического разбиения плоскости; названы по имени английского математика Роджера Пенроуза, исследовавшего их в 1970-е годы.

Перестановочный многогранник порядка 




Шоссе, Шоссейная дорога или Шоссированная дорога — широкая скоростная дорога с твёрдым искусственным покрытием поверх грунтового основания и с канавами для стока дождевой воды по обочинам.
Группа симметрии некоторого объекта ― группа всех преобразований, для которых данный объект является инвариантом, с композицией в качестве групповой операции. Как правило, рассматриваются множества точек n-мерного евклидова пространства и движения этого пространства, но понятие группы симметрии сохраняет свой смысл и в более общих случаях.

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.

Рафаэль Митчел Робинсон — американский математик, внёсший большой вклад в развитие математической логики.

Замощение Фодерберга — замощение плоскости одинаковыми (конгруэнтными) девятиугольными плитками особой формы по спирали без промежутков и перекрытий. Первое открытое спиральное замощение; найдено в 1936 году немецким математиком Хайнцем Фодербергом.

Пятиугольный паркет — в геометрии: замощение, составленное из выпуклых пятиугольников. Замощение из правильных пятиугольников в евклидовом пространстве невозможно, поскольку общий угол правильного пятиугольника равен 108° и не делит ни 180°, ни 360°. Однако ими можно замостить гиперболическую плоскость и сферу.

Мозаика «сфинкс» — замощение плоскости посредством «сфинксов» — пятиугольных гексиамондов, образованных соединением шести правильных треугольников. Полученная фигура названа по её схожести с Большим сфинксом в Гизе.

Число Хееша фигуры — максимальное число слоёв копий той же фигуры, которые могут её окружать. Задача Хееша — это задача определения набора чисел, которые могут быть числами Хееша. И то, и другое названы именем немецкого геометра Генриха Хееша, который нашёл мозаику с числом Хееша 1 и предложил более общую задачу.

Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.

Замощение плитками домино области в евклидовой плоскости — мозаика из плиток домино, которые образованы объединением двух единичных квадратов, соединённых по ребру. Эквивалентно — это паросочетание в графе решётки, образованное помещением вершины в центр каждого квадрата области и соединением двух вершин, если два соответствующих квадрата смежны.

Треугольные призматические соты — замощение трёхмерного пространства. Соты состоят полностью из треугольных призм.

Многогранник Часара — невыпуклый многогранник, топологически эквивалентный тору, с 14 треугольными гранями.

Пифагорова мозаика — замощение евклидовой плоскости квадратами двух различных размеров, в которой каждый квадрат касается четырёх квадратов другого размера своими четырьмя сторонами. Исходя из этой мозаики, можно доказать (наглядно) теорему Пифагора, за что мозаика и получила название пифагоровой. Мозаика часто используется в качестве узора для кафельного пола. В этом контексте мозаика известна также как узор классов.
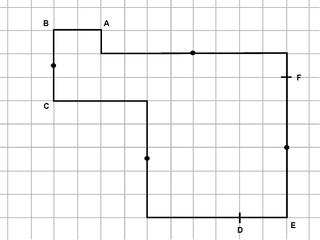
Критерий Конвея — набор условий, при выполнении которых протоплитка замощает плоскость. Назван по имени английского математика Джона Хортона Конвея. Выполнение критерия Конвея является достаточным, но не обязателеным условием для замощения плоскости.

Апериодичная мозаика — это непериодичное замощение с дополнительным свойством, что замощение не содержит бесконечно больших периодических кусков. Множество типов плиток является набором непериодичных протоплиток, если копии этих плиток могут образовать только апериодичные мозаики. Мозаики Пенроуза являются наиболее известными примерами апериодичных мозаик.

Плитка Соколара — Тейлор — это одиночная плитка, которая апериодична на плоскости, что означает, что возможны только непериодичные замощения на плоскости при разрешении вращения и зеркального отражения. Плитка была первым примером одиночной апериодичной плитки, или «einstein». Плитка Соколара — Тейлор строится на основе правильного шестиугольника с некоторым узором для обеспечения локального правила соединения. Чтобы реализовать это локальное правило без условий на узор, плитка является несвязной, так как это правило не может быть геометрически реализовано в двухмерном пространстве в виде связной плитки. Из-за этого, для полного решения «Задачи одной плитки» в двумерном пространстве потребовались другие техники.