У́гол — геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Практическое построение окружности возможно с помощью циркуля. Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки, в зависимости от подхода, круг может включать или не включать.
Постоя́нная, или конста́нта — постоянная величина в математике, физике, химии. Чтобы показать постоянство величины C, обычно пишут
 .
.
Пери́метр — общая длина границы фигуры. Имеет ту же размерность величин, что и длина.

Центроид треугольника — точка пересечения медиан в треугольнике.

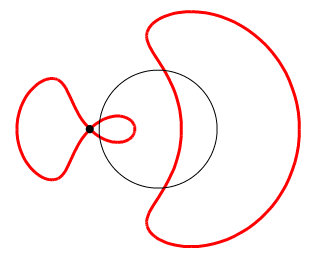
Вершина кривой — точка кривой, в которой первая производная кривизны равна нулю. Как правило, это локальный максимум или минимум кривизны и некоторые авторы определяют вершину как экстремальную точку кривизны, то есть максимум или минимум кривизны. Различие определений проявляется, например, когда вторая производная кривизны равна нулю.

Задача о перемещении дивана была сформулирована канадским математиком австрийского происхождения Мозером в 1966 году.

Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг. Поскольку окружность является границей круга или диска, длина окружности является частным случаем периметра.
Изопериметри́ческое нера́венство — геометрическое неравенство, связывающее периметр замкнутой кривой на плоскости и площадь участка плоскости, ограниченной этой кривой. Этот термин также используется для различных обобщений данного неравенства.

Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это такая окружность, по отношению к которой каждая сторона описанного многоугольника является касательной. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.

Треугольник Рёло́ представляет собой область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Негладкая замкнутая кривая, ограничивающая эту фигуру, также называется треугольником Рёло.
В математике константой Чигера графа называется числовая характеристика графа, отражающая, есть ли у графа «узкое место» или нет. Константа Чигера как способ измерения наличия «узкого места» представляет интерес во многих областях, например, для создания сильно связанных компьютерных сетей, для тасования карт и в топологии малых размерностей. Названа в честь математика Джефа Чигера.
Изопериметрическая константа Чигера компактного риманова многообразия M — положительное вещественное число h(M), определяемое через минимальную площадь гиперповерхности, которая делит M на две непересекающиеся части равного объёма. В 1970-м году Джеф Чигер доказал неравенство, связывающее первое нетривиальное собственное число оператора Лапласа — Бельтрами на M с числом h(M). Это доказательство оказало большое влияние на риманову геометрию и способствовало созданию аналогичной концепции в теории графов.
Спектральная теория графов — направление в теории графов, изучающее свойства графов, характеристических многочленов, собственных векторов и собственных значений матриц, связанных с графом, таких, как его матрица смежности или матрица Кирхгофа.
Формула Крофтона — классический результат интегральной геометрии. Связывает длину кривой со средним числом пересечений с прямыми.

Теорема Микеля — утверждение в планиметрии, связанное с пересечением трёх окружностей, построенных вокруг вершин треугольника. Названа в честь французского математика Огюста Микеля. Эта теорема — один из нескольких результатов, касающийся окружностей в геометрии, полученный Микеле и опубликованных им в Journal de mathématiques pures et appliquées.

Парадокс береговой линии — противоречивое наблюдение в географических науках, связанное с невозможностью точно определить длину линии побережья из-за её фракталоподобных свойств. Первое задокументированное описание данного феномена было сделано Льюисом Ричардсоном; впоследствии оно было расширено Бенуа Мандельбротом.
Кривая моментов — алгебраическая кривая в d-мерном евклидовом пространстве, заданная множеством точек с декартовыми координатами