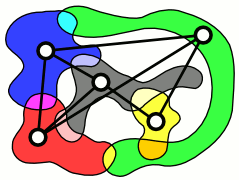
Индифферентный граф

Индифферентный граф — это неориентированный граф, построенный путём назначения вещественного числа каждой вершине и соединения двух вершин ребром, когда их числа отличаются не более чем на единицу^[1]. Индифферентные графы являются также графами пересечений множеств единичных отрезков или интервалов с определённым свойством вложения (никакой интервал не содержит какой-либо другой). Основываясь на этих двух типах интервальных представлений, эти графы называются также графами единичных отрезков или собственными интервальными графами. Индифферентные графы образуют подкласс интервальных графов.

Конечные индифферентные графы можно эквивалентно описать как

• Графы пересечений единичных отрезков^[1]
• Графы пересечений множеств интервалов, никакие два из которых не вложены друг в друга^[1][2]
• Интервальные графы без клешней^[1][2]
• Графы, не содержащие порождённых подграфов, изоморфных клешне K_1,3, «сети» (треугольника с тремя дополнительными вершинами, присоединёнными к каждой вершине треугольника), «солнцу» (треугольнику с тремя присоединёнными треугольниками, имеющими общие рёбра с центральным треугольником), или «дыры» (циклы длины четыре и более)^[3]
• Графы несравнимости полупорядков^{[англ.][1]}
• Неориентированные графы, которые имеют линейный порядок, такой, что для каждого пути из трёх вершин ${\displaystyle uvw}$, вершины которого упорядочены ${\displaystyle u}$–${\displaystyle v}$–${\displaystyle w}$, конечные вершины ${\displaystyle u}$ и ${\displaystyle w}$ смежны ^[4]
• Графы, не имеющие астральных троек, трёх вершин, соединённых попарно путями, не проходящими через третью вершину, а также не содержащие двух смежных вершин, одновременно смежных вершине из окрестности третьей вершины ^[5].
• Графы, в которых каждая компонента содержит путь, в котором каждая клика компоненты образует непрерывный подпуть^[6]
• Графы, вершины которых могут быть пронумерованы таким образом, что любой кратчайший путь образует монотонную последовательность^[6]
• Графы, матрицы смежности которых могут быть упорядочены так, что в каждой строке и каждом столбце ненулевые элементы образуют непрерывные интервалы, смежные диагонали матрицы^[7]
• Порождённые подграфы степеней безхордовых путей^[8]
• Листовые степени^[англ.], имеющие листовой корень^[англ.] в виде гусеницы^[8]

Для бесконечных графов некоторые из этих определений могут дать различные графы.

Поскольку индифферентные графы являются частным случаем интервальных графов, индифферентные графы имеют все свойства интервальных графов. В частности, они являются специальным случаем хордальных графов и совершенных графов. Эти графы являются также специальным случаем круговых графов, что неверно для интервальных графов общего вида.

В модели Эрдёша — Реньи случайных графов граф с ${\displaystyle n}$ вершины, число рёбер которого существенно меньше ${\displaystyle n^{2/3}}$, будет с большой вероятностью индифферентным графом, в то время как графы с числом рёбер, существенно большим ${\displaystyle n^{2/3}}$, с большой вероятностью не будет индифферентным графом^[9].

Ширина ленты^[англ.] произвольного графа ${\displaystyle G}$ на единицу меньше размера наибольшей клики в индифферентном графе, который содержит ${\displaystyle G}$ в качестве подграфа и выбран для минимизации размера наибольшей клики^[10]. Это свойство образует параллели, подобные связи между путевой шириной и интервальными графами, а также между древесной шириной и хордальными графами. Более слабое понятие ширины, кликовая ширина, может быть произвольно большой на индифферентных графах^[11]. Однако любой собственный подкласс индифферентных графов, не замкнутый относительно порождённых подграфов, имеет ограниченную кликовую ширину^[12].

Любой связный индифферентный граф содержит гамильтонов путь^[13]. Индифферентный граф имеет гамильтонов граф тогда и только тогда, когда он двусвязен^[14].

Индифферентные графы удовлетворяет гипотезе о реконструкции^[англ.] — они единственным образом определяются их подграфами с удалённой вершиной^[15].

Как и с многомерными графами единичных дисков, можно преобразовать множество точек в их индифферентный граф или множество единичных отрезков в их граф единичных отрезков за линейное время, если измерять в терминах размера выходного графа. Алгоритм округляет точки (или центры интервалов) к ближайшему меньшему целому числу, использует хеш-таблицу для нахождения всех пар точек, чьи округлённые значения отличаются не более чем на единицу (задача поиска ближайшего соседа с фиксированным радиусом), и отбирает в полученном списке пары, неокруглённые значения которых находятся не далее чем на единицу друг от друга^[16].

Можно проверить, является ли данный граф индифферентным за линейное время с помощью PQ-деревьев для построения интервальных представлений графа и затем проверки, удовлетворяет ли упорядочение вершин, производное от этого представления, свойствам индифферентного графа^[4]. Можно также основать алгоритм распознавания для индифферентных графов на алгоритмах распознавания для хордального графа^[14]. Некоторые альтернативные алгоритмы распознавания за линейное время основываются на поиске в ширину или на лексикографическом поиске в ширину, а не на связи между индифферентными графами и интервальными графами^{[17][18][19][20]}.

Как только вершины отсортированы по их числовым значениям, которые описывают индифферентный граф (или по последовательности единичных отрезков в интервальном представлении), тот же самый порядок можно использовать для поиска оптимальной раскраски этих графов, чтобы решить задачу о кратчайшем пути, построения гамильтоновых путей и наибольших паросочетаний за линейное время^[4]. Гамильтонов цикл можно найти из правильного интервального графа представления за время ${\displaystyle O(n\log n)}$^[13], но если граф является входным для задачи, та же задача может быть решена за линейное время, что может быть обобщено на интервальные графы^[21][22].

Предписанная раскраска остаётся NP-полной, даже когда она ограничена индифферентными графами^[23]. Однако она является фиксированно-параметрически разрешимой^[англ.], если параметризовать по общему числу цветов на входе^[12].

В математической психологии индифферентные графы возникают из функций полезности путём масштабирования функции так, что одна единица представляет разность в полезности достаточно малой, так что для личности единица может рассматриваться как несущественная. В этом приложении пары элементов, полезности которых достаточно велики, могут быть частично упорядочены по относительному порядку полезности, что даёт полупорядок^{[англ.] [1][24]}.

В биоинформатике задача добавления раскрашенного графа к правильно раскрашенному графу единичных отрезков может быть использована для моделирования обнаружения ложноотрицательных сборок генома ДНК из фрагментов^[25].

• Пороговый граф, a graph whose edges are determined by sums of vertex labels rather than differences of labels
• Тривиально совершенный граф, интервальные графы for which every pair of intervals is nested or disjoint rather than properly intersecting

• Information System on Graph Class Inclusions: unit interval graph