Интерполянт

О способе нахождения промежуточных значений см. Интерполяция.

Интерполянт или интерполирующая функция — в вычислительной математике это функция, которая строится по значениям в некоторых точках. Эта функция может быть использована для того, чтобы приблизить значение новых точек.

Пример

Пусть будет известна функция $g:D\rightarrow \mathbb {R}$ и $D=\{0,1\}\subset \mathbb {R}$ , а также

g(0)=1

g(1)=2

Проведя простую линейную интерполяцию мы находим интерполянт $f:D\rightarrow \mathbb {R}$ и $D=[0,1]\subset \mathbb {R}$ :

f(x)=x+1

с помощью которого мы можем аппроксимировать значения между 0 и 1. Например $f(0{,}3)=1{,}3$ .

Похожие исследовательские статьи

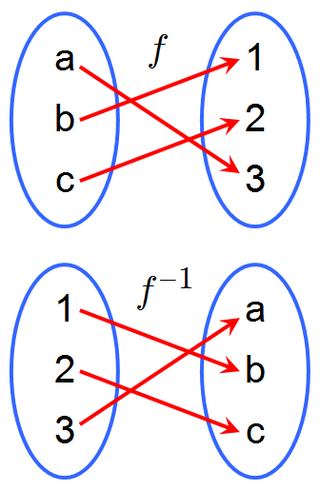
Фу́нкция — соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого.

<span class="mw-page-title-main">Предел функции</span> величина, к которой значение функции стремится при стремлении её аргумента к данной точке

Преде́лом фу́нкции в точке, предельной для области определения функции, называется такая величина, к которой значение рассматриваемой функции стремится при стремлении её аргумента к данной точке. Одно из основных понятий математического анализа.

Непрерывная функция — функция, которая меняется без мгновенных «скачков», то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.

Интерполя́ция, интерполи́рование — в вычислительной математике нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору её известных значений, определенным способом. Термин «интерполяция» впервые употребил Джон Валлис в своём трактате «Арифметика бесконечных» (1656).

Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их исхода (появления).

Голоморфная функция, иногда называемая регулярной функцией — функция комплексного переменного, определённая на открытом подмножестве комплексной плоскости $\text{[math]}$ и комплексно дифференцируемая в каждой точке.

<span class="mw-page-title-main">Интеграл Лебега</span>

Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций.

Моното́нная фу́нкция — функция одной переменной, определённая на некотором подмножестве действительных чисел, которая либо везде не убывает, либо везде не возрастает. Более точно, это функция $\text{[math]}$ , приращение которой $\text{[math]}$ при $\text{[math]}$ не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение $\text{[math]}$ не равно нулю, то функция называется стро́го моното́нной.

<span class="mw-page-title-main">Чётность функции</span> функции, обладающие симметрией относительно изменения знака аргумента

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция $\text{[math]}$ чётна, когда $\text{[math]}$ чётно, и нечётна, когда $\text{[math]}$ нечётно.

Ле́мма Фату́ — техническое утверждение, используемое при доказательстве различных теорем в функциональном анализе и теории вероятностей. Оно даёт одно из условий, при которых предел почти всюду сходящейся функциональной последовательности будет суммируемым.

Фу́нкция вероя́тности в теории вероятностей — функция возвращающая вероятность того, что дискретная случайная величина $\text{[math]}$ примет определённое значение. Например, пусть $\text{[math]}$ функция вероятности, тогда вероятность того что $\text{[math]}$ примет значение равное 13, вычисляется подстановкой значения $\text{[math]}$ в функцию $\text{[math]}$ , которая уже возвращает вероятность, например, 0.5 - это означает, что $\text{[math]}$ будет принимать значения равные 13 в 50% всех исходов.

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции $\text{[math]}$ обычно обозначается $\text{[math]}$ , иногда также используется обозначение $\text{[math]}$ .

В математике, поточечная сходимость последовательности функций на множестве — это вид сходимости, при котором каждой точке данного множества ставится в соответствие предел последовательности значений элементов последовательности в этой же точке.

<span class="mw-page-title-main">Полунепрерывная функция</span>

Полунепреры́вность в математическом анализе — это свойство функции более слабое, чем непрерывность. Функция полунепрерывна снизу в точке, если значения функции в близких точках не сильно меньше значения функции в ней. Функция полунепрерывна сверху в точке, если значения функции в близких точках не сильно превышают значения функции в ней.

Числова́я фу́нкция — функция, которая действует из одного числового пространства (множества) в другое числовое пространство (множество). Числовые множества — это множества натуральных, целых, рациональных, вещественных и комплексных чисел вместе с определёнными для соответствующих множеств алгебраическими операциями. Для всех перечисленных числовых множеств, кроме комплексных чисел, определено также отношение линейного порядка, позволяющее сравнивать числа по величине. Числовые пространства — это числовые множества вместе с функцией расстояния, заданной на соответствующем множестве.

Кватернионный анализ — это раздел математики, изучающий регулярные кватернионнозначные функции кватернионного переменного. Из-за некоммутативности алгебры кватернионов существуют различные неравносильные подходы к определению регулярных кватернионных функций. В данной статье будет рассматриваться, в основном, подход Фютера.

Многозначное отображение — разновидность математического понятия отображения (функции). Пусть $\text{[math]}$ и $\text{[math]}$ — произвольные множества, а $\text{[math]}$ — совокупность всех подмножеств множества $\text{[math]}$ Многозначным отображением из множества $\text{[math]}$ в $\text{[math]}$ называется всякое отображение $\text{[math]}$ Обычно областью определения многозначного отображения $\text{[math]}$ является подмножество $\text{[math]}$ , а областью значений — пространство $\text{[math]}$ состоящее из непустых компактных подмножеств множества $\text{[math]}$ то есть $\text{[math]}$

Пример 1. Пусть $\text{[math]}$ . Ставя в соответствие каждому значению $\text{[math]}$ отрезок $\text{[math]}$ мы получаем многозначное отображение $\text{[math]}$

Пример 2. Пусть $\text{[math]}$ — непрерывная функция. Положим $\text{[math]}$ и $\text{[math]}$ Ставя в соответствие каждому значению $\text{[math]}$ множество $\text{[math]}$ мы получаем многозначное отображение $\text{[math]}$

Пример 3. Контингенция и паратингенция.

Квазивыпуклая функция — обобщение понятия выпуклой функции, нашедшее широкое применение в нелинейной оптимизации, в частности, при применении оптимизации к вопросам экономики.

Арифметическая комбинаторика — междисциплинарная область математики, изучающая зависимость между структурами, образуемыми в поле операцией сложения и операцией умножения.

Вещественно-аналитическая функция — вещественная функция, представимая в окрестности каждой точки степенным рядом. Эквивалентное определение: вещественная функция, равная в окрестности каждой точки области определения своему ряду Тейлора.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.