Инъективный объект

Инъективный объект — теоретико-категорное обобщение понятия инъективного модуля. Двойственное понятие — проективный объект.

Объект ${\displaystyle Q}$ категории ${\displaystyle C}$ называется инъективным, если для любого морфизма ${\displaystyle f:A\to Q}$ и любого мономорфизма ${\displaystyle h:A\to B}$ существует морфизм ${\displaystyle g:B\to Q}$ продолжающий ${\displaystyle f}$, то есть ${\displaystyle g\circ h=f}$.

Исходное определение инъективного объекта было дано для абелева случая (и он остаётся наиболее важным). Если ${\displaystyle C}$ — абелева категория, то её объект ${\displaystyle Q}$ называется инъективным тогда и только тогда, когда функтор Hom ${\displaystyle \mathrm {Hom} _{C}(-,Q)}$ точен.

Говорят, что в категории ${\displaystyle C}$ достаточно много инъективных объектов, если для любого объекта ${\displaystyle X}$ категории ${\displaystyle C}$ существует мономорфизм ${\displaystyle f:X\to Q}$ в инъективный объект ${\displaystyle Q}$.

Мономорфизм ${\displaystyle g}$ категории ${\displaystyle C}$ называется существенным, если для любого морфизма ${\displaystyle f}$ композиция ${\displaystyle f\circ g}$ является мономорфизмом, только если ${\displaystyle f}$ является мономорфизмом.

Если ${\displaystyle f:X\to G}$ — существенный мономорфизм и объект ${\displaystyle G}$ инъективен, то ${\displaystyle G}$ называется инъективной оболочкой ${\displaystyle X}$. Инъективная оболочка единственна с точностью до неканонического изоморфизма.

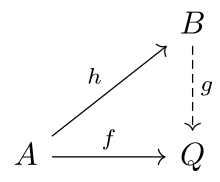
Пусть ${\displaystyle {\mathfrak {C}}}$ является категорией ${\displaystyle {\mathcal {H}}}$ — Класс морфизмов у ${\displaystyle {\mathfrak {C}}}$.

Объект ${\displaystyle Q}$ категории ${\displaystyle {\mathfrak {C}}}$ называется ${\displaystyle {\mathcal {H}}}$-иньективним если для любого морфизма ${\displaystyle f:\to Q}$ и каждого морфизма ${\displaystyle h:\to B}$ из класса ${\displaystyle {\mathcal {H}}}$ существует морфизм ${\displaystyle g:B\to Q}$ для которого ${\displaystyle g\circ h=f}$.

Если ${\displaystyle {\mathcal {H}}}$ является классом мономорфизм то получается определение иньективних модулей.

Категория ${\displaystyle {\mathfrak {C}}}$ имеет довольно много ${\displaystyle {\mathcal {H}}}$-иньективних объектов если для каждого объекта X категории ${\displaystyle {\mathfrak {C}}}$, существует ${\displaystyle {\mathcal {H}}}$-морфизм с X в ${\displaystyle {\mathcal {H}}}$-иньективний объект.

• В категории абелевых групп инъективные объекты — это делимые группы.

• В категории модулей ${\displaystyle R-\mathrm {Mod} }$ инъективные объекты — это инъективные модули. В ${\displaystyle R-\mathrm {Mod} }$ существуют инъективные оболочки, и, как следствие, достаточно много инъективных объектов.

• В категории метрических пространств и коротких отображений инъективные объекты по отношению к экстремальным мономорфизмам — это инъективные метрические пространства.

• Рассматривают также инъективные объекты в более общих категориях, например в категориях функторов или в категориях пучков модулей.

${\displaystyle {\mathcal {H}}}$-морфизм g в ${\displaystyle {\mathfrak {C}}}$ называется ${\displaystyle {\mathcal {H}}}$-существенным если для любого морфизма f, композиция fg принадлежит классу ${\displaystyle {\mathcal {H}}}$ только если f принадлежит классу ${\displaystyle {\mathcal {H}}}$.

Если g есть ${\displaystyle {\mathcal {H}}}$-существенным морфизм с X в ${\displaystyle {\mathcal {H}}}$-иньективний объект G, то G называется H-иньективною оболочкой объекта X.

• Jiri Rosicky. Injectivity and accessible categories.
• Charles A. Weibel. An Introduction to Homological Algebra. — Cambridge University Press, 1994.