Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
Ко́мпле́ксный ана́лиз, тео́рия фу́нкций ко́мпле́ксного переме́нного — раздел математического анализа, в котором рассматриваются и изучаются функции комплексного аргумента.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.

Соприкаса́ющаяся окру́жность, окру́жность кривизны́ — окружность, являющаяся наилучшим приближением заданной кривой в окрестности данной точки. В этой точке кривая и означенная окружность имеют касание, порядок которого не ниже 2. Окружность кривизны существует в каждой точке дважды дифференцируемой кривой с отличной от нуля кривизной; в случае нулевой кривизны в качестве соприкасающейся надлежит рассматривать касательную прямую — «окружность бесконечного радиуса».

Теоре́ма Мёнье́ — даёт выражение для кривизны кривой, лежащей на поверхности.
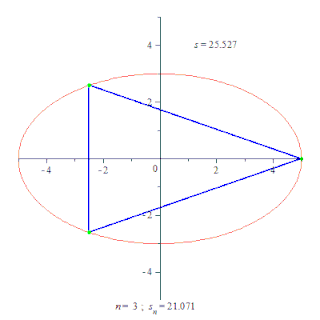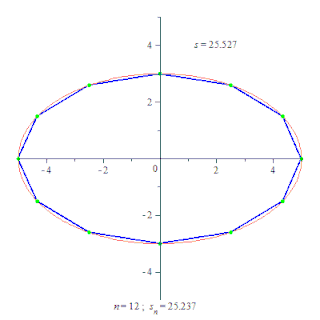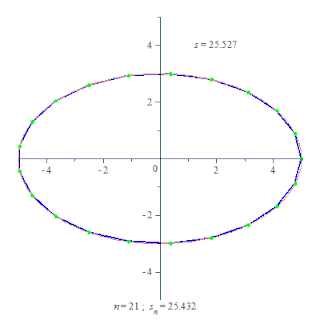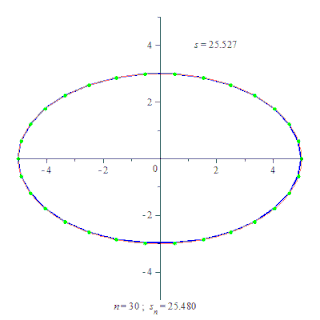
Длина́ криво́й — числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой.
Секущая — это прямая, которая пересекает кривую в двух точках, а также прямая, пересекающая две другие компланарные прямые в двух разных точках.
Теорема Лежандра в сферической тригонометрии позволяет упростить решение сферического треугольника, если известно, что его стороны достаточно малы по сравнению с радиусом сферы, на которой он расположен.
Исторический термин «решение треугольников» обозначает решение следующей тригонометрической задачи: найти остальные стороны и/или углы треугольника по уже известным. Существуют также обобщения этой задачи на случай, когда заданы другие элементы треугольника, а также на случай, когда треугольник располагается не на евклидовой плоскости, а на сфере, на гиперболической плоскости и т. п. Данная задача часто встречается в тригонометрических приложениях — например, в геодезии, астрономии, строительстве, навигации.
Лемма Синга — ключевое утверждение о стабильности замкнутых геодезических в римановых многообразиях с положительной секционной кривизной.
Субри́маново многообра́зие — математическое понятие, обобщающее риманово многообразие. Суть обобщения состоит в том, что скалярное произведение задается не на касательных пространствах целиком, а только на некоторых их подпространствах.
Формула Крофтона — классический результат интегральной геометрии. Связывает длину кривой со средним числом пересечений с прямыми.

Лемма о руке — лемма в доказательстве теоремы Коши о многогранниках.
Замкнутая геодезическая на римановом многообразии — это геодезическая, которая образует простую замкнутую кривую. Её можно формализовать как проекцию замкнутой орбиты геодезического потока на касательное пространство многообразия.

Вариация поворота кривой — интеграл кривизны кривой по её длине.
Теорема Усова о геодезической даёт точную оценку на вариацию поворота геодезической на графике выпуклой липшицевой функции.
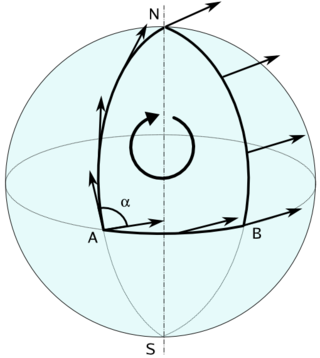
Голоно́ми́я — один из инвариантов связности в расслоении над гладким многообразием, сочетающий свойства кривизны и монодромии, и имеющий важное значение как в геометрии, так и геометризированных областях естествознания, таких как теория относительности и теория струн. Обыкновенно речь идёт о голономии связностей в векторном расслоении, хотя в равной степени имеет смысл говорить о голономии связности в главном расслоении или даже голономии связности Эресманна в локально тривиальном топологическом расслоении.