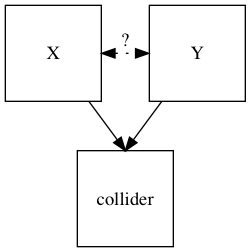
Каузальная циклическая диаграмма

Каузальная циклическая диаграмма (CLD) — это каузальная диаграмма, которая помогает визуализировать взаимосвязь различных переменных в системе. Схема состоит из множества узлов и ребер. Узлы представляют переменные, а ребра — связи, которые представляют связь или отношение между двумя переменными. Ссылка, отмеченная положительно, указывает на положительное отношение, а ссылка, отмеченная отрицательно, указывает на отрицательное отношение. Положительная причинно-следственная связь означает, что два узла изменяются в одном направлении, то есть если узел, в котором начинается связь, уменьшается, другой узел также уменьшается. Аналогично, если узел, в котором начинается связь, увеличивается, то увеличивается и другой узел. Отрицательная причинно-следственная связь означает, что два узла изменяются в противоположных направлениях, то есть если узел, в котором начинается связь, увеличивается, то другой узел уменьшается и наоборот.
Замкнутые циклы на диаграмме являются очень важными особенностями CLD. Замкнутый цикл определяется как усиливающий или уравновешивающий контур обратной связи. Усиливающая петля — это цикл, в котором эффект изменения любой переменной распространяется через петлю и возвращается к переменной, усиливающей начальное отклонение, то есть если переменная увеличивается в усиливающей петле, то эффект через цикл будет возвращать увеличение той же переменной и наоборот. Уравновешивающий цикл — это цикл, в котором эффект изменения какой-либо переменной распространяется через цикл и возвращает переменной отклонение, противоположное исходному, то есть если переменная увеличивается в уравновешивающем цикле, то эффект через цикл возвращает уменьшение той же переменной и наоборот[1].
Если переменная изменяется в усиливающем цикле, эффект изменения усиливает первоначальное изменение. Затем он создаст ещё один усиливающий эффект. Не разорвав петлю, система попадет в порочный круг круговых цепных реакций. По этой причине замкнутые контуры являются критическими характеристиками CLD.
Пример положительной обратной связи:
- Сумма на банковском балансе будет влиять на сумму заработанных процентов, представленную на диаграмме верхней синей стрелкой.
- Поскольку увеличение банковского баланса приводит к увеличению заработанных процентов, эта связь положительна и обозначается знаком «+».
- Заработанные проценты добавляются к банковскому балансу, это также положительная ссылка, представленная нижней синей стрелкой.
- Причинно-следственный эффект между этими узлами образует положительную усиливающую циклическую связь, представленную зелёной стрелкой, которая обозначается буквой «R»[2].
История
Использование узлов и стрелок для построения ориентированных графовых моделей причинно-следственных связей восходит к изобретению метода анализа путей[англ.] Сьюаллом Райтом в 1918 году, задолго до системной динамики. Однако из-за ограниченности генетических данных эти ранние причинные графы не содержали петель —они были направленными ациклическими графами. Первое формальное использование диаграмм причинных петель было объяснено доктором Деннисом Медоуз на конференции для педагогов[3].
Медоуз объяснил, что когда он и другие исследователи работали над моделью World3[англ.], они поняли, что не смогут использовать компьютерный вывод, чтобы объяснить, как работают петли обратной связи в их модели при представлении своих результатов другим. Они решили показать петли обратной связи, используя стрелки, соединяющие названия основных компонентов модели в петлях обратной связи. Возможно, это было первое формальное использование диаграмм причинно-следственных связей.
Положительные и отрицательные причинно-следственные связи
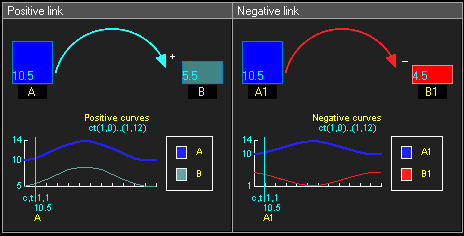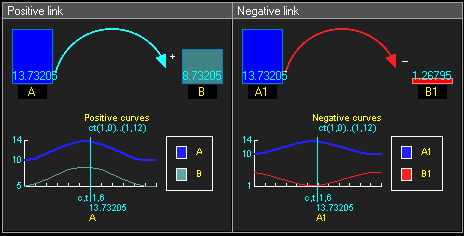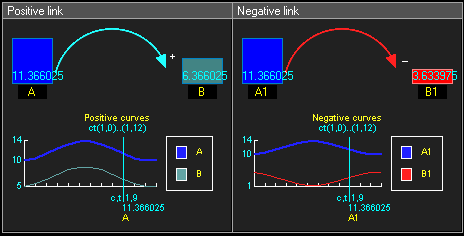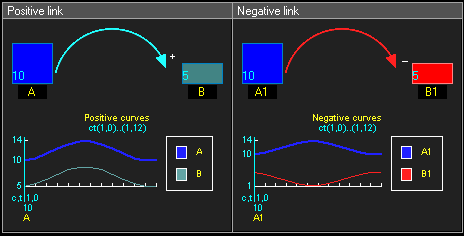
Положительная причинно-следственная связь означает, что два узла изменяются в одном направлении, то есть если узел, в котором начинается связь, уменьшается, то уменьшается и другой узел. Аналогично, если узел, в котором начинается связь, увеличивается, то увеличивается и другой узел.
Отрицательная причинно-следственная связь означает, что два узла изменяются в противоположных направлениях, то есть если узел, в котором начинается связь, увеличивается, то другой узел уменьшается, и наоборот.
Усиливающие и балансирующие циклы
Чтобы определить, является ли каузальный цикл усиливающим или балансирующим, можно начать с предположения, например, «Узел 1 увеличивается», и следовать вокруг цикла[4]. Усиливающие циклы имеют четное число отрицательных связей, а балансирующие — нечетное.
Выявление усиливающих и балансирующих циклов является важным шагом для выявления эталонных моделей поведения, то есть возможных динамических моделей поведения системы. Усиливающие петли связаны с экспоненциальным увеличением/уменьшением.
Балансирующие циклы связаны с достижением плато. Если система имеет задержки (часто обозначаемые путем проведения короткой линии через причинно-следственную связь), то она может колебаться.
Примеры

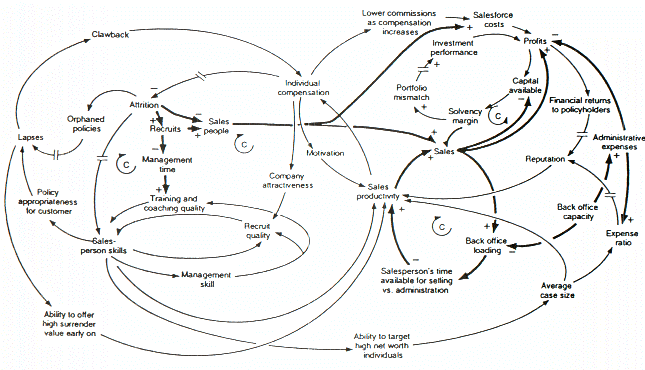
Примечания
- ↑ Causal Loop Diagrams: Little Known Analytical Tool (амер. англ.). iSixSigma (26 февраля 2010). Дата обращения: 22 марта 2021. Архивировано 22 апреля 2021 года.
- ↑ John Sterman. System Dynamics: Systems Thinking and Modeling for a Complex World (англ.). — Massachusetts Institute of Technology. Engineering Systems Division, 2002-05. Архивировано 21 января 2022 года.
- ↑ Creative Learning Exchange —. www.clexchange.org. Дата обращения: 22 марта 2021. Архивировано 14 апреля 2021 года.
- ↑ Causal Loop Construction: The Basics (англ.). The Systems Thinker (11 января 2016). Дата обращения: 22 марта 2021. Архивировано 19 марта 2021 года.